Определим тяговое усилие, на каждой передаче Н
 , (1.6.1)
, (1.6.1)
где  – передаточное число i-ой передачи.
– передаточное число i-ой передачи.
Для примера рассчитаем  на 1-ой передаче при
на 1-ой передаче при 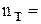 500
500  :
:
 4047,9 Н
4047,9 Н
Остальные значения  вычисляются аналогично, результаты расчёта заносятся в таблицу 1.6.1.
вычисляются аналогично, результаты расчёта заносятся в таблицу 1.6.1.
Таблица 1.6.1 – Тяговая характеристика автомобиля
| Передача | Параметр | Частота вращения коленчатого вала двигателя | |||||||||||
| I | Рт, Н | 4047,9 | 4295,1 | 4480,5 | 4604,1 | 4665,9 | 4665,9 | 4604,1 | 4480,5 | 4295,1 | 4047,9 | 3738,9 | 3368,1 |
| Vа. м/с | 1,0 | 1,9 | 2,9 | 3,9 | 4,9 | 5,8 | 6,8 | 7,8 | 8,8 | 9,7 | 10,7 | 11,7 | |
| II | Рт, Н | 2550,2 | 2705,9 | 2822,7 | 2900,6 | 2939,5 | 2939,5 | 2900,6 | 2822,7 | 2705,9 | 2550,2 | 2355,5 | 2121,9 |
| Vа. м/с | 1,5 | 3,1 | 4,6 | 6,2 | 7,7 | 9,3 | 10,8 | 12,3 | 13,9 | 15,4 | 17,0 | 18,5 | |
| III | Рт, Н | 1619,2 | 1718,0 | 1792,2 | 1841,6 | 1866,4 | 1866,4 | 1841,6 | 1792,2 | 1718,0 | 1619,2 | 1495,6 | 1347,2 |
| Vа. м/с | 2,4 | 4,9 | 7,3 | 9,7 | 12,2 | 14,6 | 17,0 | 19,4 | 21,9 | 24,3 | 26,7 | 29,2 | |
| IV | Рт, Н | 1012,0 | 1073,8 | 1120,1 | 1151,0 | 1166,5 | 1166,5 | 1151,0 | 1120,1 | 1073,8 | 1012,0 | 934,7 | 842,0 |
| Vа. м/с | 3,9 | 7,8 | 11,7 | 15,6 | 19,4 | 23,3 | 27,2 | 31,1 | 35,0 | 38,9 | 42,8 | 46,7 |
Определим скорость движения автомобиля на каждой передаче, м/с
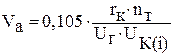 . (1.6.2)
. (1.6.2)
Для примера рассчитаем  на 1-ой передаче при
на 1-ой передаче при 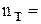 500
500  :
:
 1 м/с
1 м/с
Остальные значения  вычисляются аналогично, результаты расчёта заносятся в таблицу 1.6.1.
вычисляются аналогично, результаты расчёта заносятся в таблицу 1.6.1.
По таблице 1.6.1 строится тяговая характеристика автомобиля, рисунок 1.2.
Тяговое усилие, подводимое к ведущим колёсам автомобиля, расходуется на преодоление сопротивлений качению, воздуха, подъёму и силам инерции.
Определим силу сопротивления воздуха на каждой передаче, Н
 . (1.6.3)
. (1.6.3)
Для примера рассчитаем  на 1-ой передаче при
на 1-ой передаче при 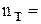 500
500  :
:
 = 0,53 Н
= 0,53 Н
Остальные значения  вычисляются аналогично, результаты расчёта заносятся в таблицу 1.6.2.
вычисляются аналогично, результаты расчёта заносятся в таблицу 1.6.2.
Таблица 1.6.2 – Тяговая характеристика с учётом сил сопротивления
| Передача | Параметр | Частота вращения коленчатого вала двигателя | |||||||||||
| I | Vа. м/с | 1,0 | 1,9 | 2,9 | 3,9 | 4,9 | 5,8 | 6,8 | 7,8 | 8,8 | 9,7 | 10,7 | 11,7 |
| Рв, Н | 0,53 | 2,11 | 4,75 | 8,44 | 13,19 | 19,00 | 25,86 | 33,77 | 42,74 | 52,77 | 63,85 | 75,99 | |
| Рвс, Н | 4047,4 | 4293,0 | 4475,7 | 4595,6 | 4652,7 | 4646,9 | 4578,2 | 4446,7 | 4252,3 | 3995,1 | 3675,0 | 3292,1 | |
| II | Vа. м/с | 1,5 | 3,1 | 4,6 | 6,2 | 7,7 | 9,3 | 10,8 | 12,3 | 13,9 | 15,4 | 17,0 | 18,5 |
| Рв, Н | 1,33 | 5,32 | 11,97 | 21,27 | 33,24 | 47,86 | 65,15 | 85,09 | 107,69 | 132,95 | 160,87 | 191,45 | |
| Рвс, Н | 2548,8 | 2700,6 | 2810,7 | 2879,3 | 2906,3 | 2891,6 | 2835,4 | 2737,6 | 2598,2 | 2417,2 | 2194,6 | 1930,4 | |
| III | Vа. м/с | 2,4 | 4,9 | 7,3 | 9,7 | 12,2 | 14,6 | 17,0 | 19,4 | 21,9 | 24,3 | 26,7 | 29,2 |
| Рв, Н | 3,30 | 13,19 | 29,68 | 52,77 | 82,45 | 118,73 | 161,60 | 211,07 | 267,14 | 329,80 | 399,06 | 474,92 | |
| Рвс, Н | 1615,9 | 1704,8 | 1762,5 | 1788,9 | 1783,9 | 1747,6 | 1680,0 | 1581,1 | 1450,9 | 1289,3 | 1096,5 | 872,3 | |
| IV | Vа. м/с | 3,9 | 7,8 | 11,7 | 15,6 | 19,4 | 23,3 | 27,2 | 31,1 | 35,0 | 38,9 | 42,8 | 46,7 |
| Рв, Н | 8,4 | 33,8 | 76,0 | 135,1 | 211,1 | 303,9 | 413,7 | 540,4 | 683,9 | 844,3 | 1021,6 | 1215,8 | |
| Рвс, Н | 1003,5 | 1040,0 | 1044,1 | 1015,9 | 955,4 | 862,5 | 737,3 | 579,8 | 389,9 | 167,7 |
Определим свободную силу тяги автомобиля на каждой передаче, Н
 . (1.6.4)
. (1.6.4)
Для примера рассчитаем  на 1-ой передаче при
на 1-ой передаче при 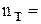 500
500  :
:
 =4047,4 Н
=4047,4 Н
Остальные значения  вычисляются аналогично, результаты расчёта
вычисляются аналогично, результаты расчёта
заносятся в таблицу 1.6.2.
По таблице 1.6.2 строится характеристика свободной тяговой силы
автомобиля, рисунок 1.3.
1.7 Определение основных показателей динамики автомобиля с механической трансмиссией
1.7.1 Динамический фактор
Универсальным измерителем динамических качеств автомобиля служит динамический фактор, представляющий отношение свободной тяговой силы к силе тяжести автомобиля.
Производим расчёт динамического фактора при движении автомобиля при оборотах коленчатого вала n=500-6000  на всех передачах:
на всех передачах:
 , (1.7.1)
, (1.7.1)
где  – свободная сила тяги автомобиля, Н.
– свободная сила тяги автомобиля, Н.
Для примера определим свободную силу тяги на первой передаче при 500  коленчатого вала:
коленчатого вала:

Результаты расчёта  сведены в таблицу 1.7.1.
сведены в таблицу 1.7.1.
Таблица 1.7.1 – Динамическая характеристика автомобиля
| Передача | Параметр | Частота вращения коленчатого вала двигателя | |||||||||||
| I | Vа. м/с | 1,0 | 1,9 | 2,9 | 3,9 | 4,9 | 5,8 | 6,8 | 7,8 | 8,8 | 9,7 | 10,7 | 11,7 |
| D | 0,30 | 0,32 | 0,34 | 0,35 | 0,35 | 0,35 | 0,34 | 0,33 | 0,32 | 0,30 | 0,28 | 0,25 | |
| II | Vа. м/с | 1,5 | 3,1 | 4,6 | 6,2 | 7,7 | 9,3 | 10,8 | 12,3 | 13,9 | 15,4 | 17,0 | 18,5 |
| D | 0,19 | 0,20 | 0,21 | 0,22 | 0,22 | 0,22 | 0,21 | 0,21 | 0,20 | 0,18 | 0,17 | 0,15 | |
| III | Vа. м/с | 2,4 | 4,9 | 7,3 | 9,7 | 12,2 | 14,6 | 17,0 | 19,4 | 21,9 | 24,3 | 26,7 | 29,2 |
| D | 0,12 | 0,13 | 0,13 | 0,13 | 0,13 | 0,13 | 0,13 | 0,12 | 0,11 | 0,10 | 0,08 | 0,07 | |
| IV | Vа. м/с | 3,9 | 7,8 | 11,7 | 15,6 | 19,4 | 23,3 | 27,2 | 31,1 | 35,0 | 38,9 | 42,8 | 46,7 |
| D | 0,0756 | 0,0783 | 0,0786 | 0,0765 | 0,0719 | 0,0650 | 0,0555 | 0,0437 | 0,0294 | 0,0126 |
По таблице 1.7.1 строится динамический характер автомобиля, рисунок 1.4.
Определим коэффициент учёта вращающихся масс на каждой передаче:
 , (1.7.2)
, (1.7.2)
где  ,
,  – эмпирические коэффициенты, в данном расчёте принимаются
– эмпирические коэффициенты, в данном расчёте принимаются
 0,05,
0,05,  0,07, согласно [2].
0,07, согласно [2].
Коэффициент учёта вращающихся масс на 1-ой передаче:

Коэффициент учёта вращающихся масс на 2-ой передаче:

Коэффициент учёта вращающихся масс на 3-ей передаче:
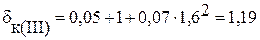
Коэффициент учёта вращающихся масс на 4-ой передаче:

Определим ускорение на горизонтальной дороге на каждой передаче, 
 , (1.7.3)
, (1.7.3)
где  – суммарный коэффициент сопротивления дороги, в данном расчёте
– суммарный коэффициент сопротивления дороги, в данном расчёте
принимается  0,015, согласно [2].
0,015, согласно [2].
Для примера рассчитаем  на 1-ой передаче при
на 1-ой передаче при 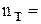 500
500  :
:
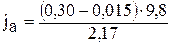 =1,31
=1,31 
Остальные значения  вычисляются аналогично, результаты расчёта заносятся в таблицу 1.7.2.
вычисляются аналогично, результаты расчёта заносятся в таблицу 1.7.2.
Таблица 1.7.2 – Прямые и обратные ускорения
| Передача | Параметр | Частота вращения коленчатого вала двигателя | |||||||||||
| I | Vа. м/с | 1,0 | 1,9 | 2,9 | 3,9 | 4,9 | 5,8 | 6,8 | 7,8 | 8,8 | 9,7 | 10,7 | 11,7 |
| jа, м/с | 1,31 | 1,39 | 1,45 | 1,50 | 1,51 | 1,51 | 1,49 | 1,44 | 1,38 | 1,29 | 1,18 | 1,05 | |
| 1/jа, с/м | 0,76 | 0,72 | 0,69 | 0,67 | 0,66 | 0,66 | 0,67 | 0,69 | 0,73 | 0,77 | 0,85 | 0,95 | |
| II | Vа. м/с | 1,5 | 3,1 | 4,6 | 6,2 | 7,7 | 9,3 | 10,8 | 12,3 | 13,9 | 15,4 | 17,0 | 18,5 |
| jа, м/с | 1,20 | 1,27 | 1,33 | 1,36 | 1,38 | 1,37 | 1,34 | 1,29 | 1,22 | 1,13 | 1,02 | 0,88 | |
| 1/jа, с/м | 0,84 | 0,79 | 0,75 | 0,73 | 0,73 | 0,73 | 0,75 | 0,77 | 0,82 | 0,89 | 0,98 | 1,13 | |
| III | Vа. м/с | 2,4 | 4,9 | 7,3 | 9,7 | 12,2 | 14,6 | 17,0 | 19,4 | 21,9 | 24,3 | 26,7 | 29,2 |
| jа, м/с | 0,88 | 0,93 | 0,97 | 0,99 | 0,98 | 0,96 | 0,92 | 0,86 | 0,78 | 0,68 | 0,56 | 0,42 | |
| 1/jа, с/м | 1,14 | 1,07 | 1,03 | 1,01 | 1,02 | 1,04 | 1,09 | 1,17 | 1,29 | 1,48 | 1,80 | 2,40 | |
| IV | Vа. м/с | 3,9 | 7,8 | 11,7 | 15,6 | 19,4 | 23,3 | 27,2 | 31,1 | 35,0 | 38,9 | 42,8 | 46,7 |
| jа, м/с | 0,53 | 0,55 | 0,56 | 0,54 | 0,50 | 0,44 | 0,35 | 0,25 | 0,13 | ||||
| 1/jа, с/м | 1,89 | 1,80 | 1,80 | 1,86 | 2,01 | 2,29 | 2,82 | 3,99 | 7,96 |
Определим величину обратных ускорений  ,
,  . Результаты расчёта
. Результаты расчёта  заносятся в таблицу 1.7.2.
заносятся в таблицу 1.7.2.
По таблице 1.7.2 строим график прямых, рисунок 1.5 и обратных ускорений, рисунок 1.6.
Определим время разгона методом графического интегрирования графика обратных ускорений. По графику величин обратных ускорений строим огибающую. Её отрезок на промежутке от 0 до 27,7 м/с (100 км/ч) делим на равные части и из центра этих отрезков проводим линии до пересечения с огибающей, проецируя их на ось обратных ускорений. Далее значения отрезков на оси  и разница между концом и началом отрезков оси абсцисс заносятся в таблицу 1.7.3.
и разница между концом и началом отрезков оси абсцисс заносятся в таблицу 1.7.3.
Таблица 1.7.3 – Интегрирование графика обратных ускорений
| № п/п |  , мм , мм
| 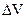 , мм , мм
| 
|
| 9,5 | 27,5 | 261,3 | |
| 9,6 | 27,5 | 264 | |
| 11,6 | 27,5 | 319 | |
| 15,1 | 27,5 | 415,3 | |
| 20,8 | 27,5 | 572 |
Определим площади отдельных фигур, заключённых под огибающей, 
 , (1.7.4)
, (1.7.4)
где  – величина обратного ускорения, мм;
– величина обратного ускорения, мм;
 – разница между концом и началом отрезка на оси абсцисс, мм.
– разница между концом и началом отрезка на оси абсцисс, мм.
Для примера рассчитаем  1-ой фигуры:
1-ой фигуры:
 =261,3
=261,3 
Остальные значения  вычисляются аналогично, результаты расчёта
вычисляются аналогично, результаты расчёта
заносятся в таблицу 1.7.3.
Определим суммарную площадь фигуры, заключенной под огибающей, 
 . (1.7.5)
. (1.7.5)


Определяем время разгона от 0 до скорости 27,7 м/с (100 км/ч), с
 ,. (1.7.6)
,. (1.7.6)
где  – суммарная площадь фигуры, заключенной под огибающей,
– суммарная площадь фигуры, заключенной под огибающей,  ;
;
а – масштаб скорости,  ;
;
b – масштаб скорости,  .
.
 с
с
Определим время разгона от скорости  до скорости
до скорости 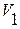 ,м/с:
,м/с:  , (1.7.7)
, (1.7.7)
где 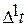 - площадь отдельной фигуры, заключённой под огибающей,
- площадь отдельной фигуры, заключённой под огибающей,  .
.

Определим время разгона от скорости 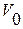 до скорости
до скорости  ,м/с
,м/с
 ,
,

Аналогично находятся  до скорости 27,7м/с.
до скорости 27,7м/с.
По полученным значениям t и графику обратных ускорений определяем значения  ; результаты сводим в таблицу 1.7.4.
; результаты сводим в таблицу 1.7.4.
Таблица 1.7.4 – Время разгона

| 0 | 5,5 | 11 | 16,5 | 22 | 27,5 |

| 0 | 2,7 | 5,8 | 9,3 | 13,8 | 20,1 |
По таблице 1.7.4 строится график времени разгона, рисунок 1.7.
На графике времени разгона принимается: для оси абсцисс
масштаб 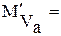
 , а для оси ординат масштаб
, а для оси ординат масштаб 

Определим путь разгона методом графического интегрирования графика времени разгона. Отрезок графика на промежутке от 0 до 27,7 м/с (100 км/ч) делим на равные части и из центра этих отрезков проводим линии до пересечения с ним, проецируя их на ось времени. Далее значения отрезков на оси  и разница между концом и началом отрезков оси абсцисс заносятся в таблицу 1.7.5.
и разница между концом и началом отрезков оси абсцисс заносятся в таблицу 1.7.5.
Таблица 1.7.5 – Интегрирование графика пути разгона
| № п/п |  , мм , мм
| 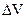 , мм , мм
| 
|
| 6,3 | 27,5 | 173,3 | |
| 21,1 | 27,5 | 580,3 | |
| 38,7 | 27,5 | 1064,3 | |
| 59,6 | 27,5 | 1639 | |
| 88,3 | 27,5 | 2428,3 |
Определим площади отдельных фигур, заключённых под графиком времени разгона, 
 , (1.7.8)
, (1.7.8)
где  – величина времени, мм.
– величина времени, мм.
Для примера рассчитаем  1-ой фигуры:
1-ой фигуры:
 =173,3
=173,3 
Остальные значения  вычисляются аналогично, результаты расчёта заносятся в таблицу 1.7.5.
вычисляются аналогично, результаты расчёта заносятся в таблицу 1.7.5.
Определим площадь фигуры, заключенной под графиком пути разгона, 
 . (1.7.9)
. (1.7.9)


Определяем путь разгона от 0 до скорости 27,7 м/с (100 км/ч), м
 . (1.7.10)
. (1.7.10)
 м
м
Определим путь разгона от скорости 0 до скорости  , м
, м
 , (1.7.11)
, (1.7.11)
где  – путь разгона от 0 до скорости
– путь разгона от 0 до скорости 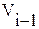 ;
;
 – площадь i-ой фигуры, заключённых под графиком,
– площадь i-ой фигуры, заключённых под графиком,  .
.
Для примера рассчитаем путь разгона от 0 до скорости 2,8 м/с:
 =8,3 м
=8,3 м
Остальные значения  вычисляются аналогично, результаты расчёта заносятся в таблицу 1.7.6.
вычисляются аналогично, результаты расчёта заносятся в таблицу 1.7.6.
Таблица 1.7.6 – Путь разгона

| 0 | 5,5 | 11 | 16,5 | 22 | 27,5 |

| 0 | 8,3 | 36,2 | 87,3 | 165,9 | 282,5 |
По таблице 1.7.6 строится график пути разгона, рисунок 1.8.