ЭЛЕМЕНТЫЭЛЕКТРИЧЕСКОЙ ЦЕПИ
СИНУСОИДАЛЬНОГО ТОКА
Электрическая цепь синусоидального тока содержит помимо электротехнических устройств, назначение которых совпадает с назначением функционально аналогичных устройств цепи постоянного тока (источники энергии, измерительные приборы, коммутационные аппараты и т.д.), также устройства, присущие только цепям синусоидального тока: трансформаторы, конденсаторы, катушки индуктивности и д.р.
Напряжения и токи в цепях синусоидального тока зависят от времени. Они называются мгновенными значениями и обозначаются строчными буквами: u и i.
Элементами схем замещения цепей синусоидального тока являются источники синусоидального (ЭДС) тока, резистивные R, индуктивные L и емкостные С элементы. Указанные элементы отображают физические процессы, протекающие в устройстве.
Резистор отображает на схеме замещения необратимые процессы преобразования электрической энергии в другие виды энергии (лучистую, тепловую, механическую).
Катушка индуктивности отображает процессы преобразования электрической энергии в энергию магнитного поля, а также явления, связанные с этим преобразованием (явление самоиндукции и взаимоиндукции). Конденсатор на схеме замещения характеризует процессы преобразования электрической энергии в энергию электрического поля, а также явления, связанные с этим преобразованием (явление заряда и разряда конденсатора).
РЕЗИСТИВНЫЙ ЭЛЕМЕНТ
При протекании электрического тока через резистор, для мгновенных значений напряжения и тока справедливо соотношение, определяемое законом Ома 
. Так как 
– постоянная величина, то амплитуды тока и напряжения связаны соотношением
, (1)
а их начальные фазы одинаковы: 
, (2)
, (3)
т.е. ток и напряжение в резистивном элементе изменяются синфазно – совпадают по фазе (рис. 1).
Разделив левую и правую части выражения (1) на 
, получим соотношение для действующих значений напряжения и тока резистивного элемента 
.
Представим теперь синусоидальный ток и напряжение резистивного элемента соответствующими комплексными значениями
.
С учетом (2) и (3) получим закон Ома в комплексной форме
(4)
ИНДУКТИВНЫЙ ЭЛЕМЕНТ
Вокруг всякого проводника с током 
существует магнитное поле. В катушке индуктивности это поле можно характеризовать магнитным потоком Ф – совокупностью непрерывных магнитных линий, т.е. линий вектора индукции В через поверхность, ограниченную замкнутым контуром. Направление магнитных линий зависит от направления намотки витков и направления тока 
. В общем случае конфигурация магнитного поля вокруг витков имеет сложную форму. Но для характеристики катушки индуктивности как элемента электрической цепи часто не требуется знать распределение магнитного поля в окружающем катушку пространстве. Достаточно вычислить потокосцепление Y магнитного потока со всеми W витками катушки
,
где 
- магнитный поток, сцепленный с k –м витком.
Основной единицей потокосцепления и магнитного потока в системе СИ служит вебер (Вб).
Потокосцепление с витками катушки зависит от тока в этой же катушке, оно называется собственным потокосцеплением 
.
Отношение собственного потокосцепления катушки к току катушки называется собственной индуктивностью или короче индуктивностью: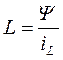 
.
Основной единицей индуктивности в системе СИ является генри (Гн), 1 Гн = 1 Вб/А.
Если в индуктивном элементе протекает синусоидальный ток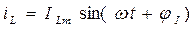 
, то по закону электромагнитной индукции на индуктивном элементе появится ЭДС самоиндукции 
, которая, на основании правила Ленца, всегда препятствует изменению тока
,
,
где амплитуды ЭДС и тока связаны соотношением 
, а их начальные фазы (рис. 2):
(5)
По II-му закону Кирхгофа 
, поэтому для действующих значений
. (6)
Величина
(7)
называется индуктивным сопротивлением, имеет размерность (Ом). 
определяет способность катушки противодействовать прохождению переменного тока. 
- индуктивная проводимость
Представим ток и напряжение в комплексной форме
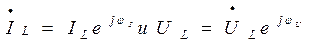или
(8)
Величина 
(9) называется комплексным сопротивлением индуктивного элемента, а обратная ей величина 
- комплексной проводимостью индуктивного элемента.
ЕМКОСТНОЙ ЭЛЕМЕНТ
Между различными частями электротехнических устройств существует электрическое поле электрических зарядов. Между обкладкам плоского конденсатора это поле имеет напряженность
,
где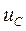 
- напряжение, а d – расстояние между обкладками конденсатора площадью S, q – заряд конденсатора, e0= 8,854 10-12 Ф/м – электрическая постоянная.
Накопленный в конденсаторе заряд q пропорционален приложенному напряжению :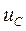
,
коэффициент пропорциональности С называется емкостью конденсатора
.
Основной единицей емкости в системе СИ является фарад (Ф), 1 Ф = 1 Кл/В = 1 А с/В.
Если напряжение между выводами емкостного элемента изменяется по синусоидальному закону 
то синусоидальный ток
,
где амплитуды связаны соотношением 
, а начальные фазы (рис. 3): 
(10)
Для действующих значений напряжения и тока емкостного элемента
. (11)
Величина 
называется емкостным сопротивлением, имеет размерность (Ом). 
- емкостная проводимость.
Закон Ома для емкостного элемента в комплексной форме:
, (12)
где величина 
, входящая в это выражение, называется комплексным сопротивлением емкостного элемента.
ЭНЕРГЕТИЧЕСКИЕ ПРОЦЕССЫВ РЕЗИСТИВНОМ,
ИНДУКТИВНОМ И ЕМКОСТНОМ ЭЛЕМЕНТЕ
Мгновенные значения мощности определяются произведением мгновенных значений тока и напряжения.
В резистивном элементе с сопротивлением r при напряжении
ток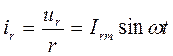 
совпадает по фазе с напряжением. Мгновенная мощность
(13)
в любой момент времени положительная, т.е. в течение любого интервала времени в резистивный элемент поступает энергия и происходит необратимое преобразование электрической энергии источника в другие ее виды (рис. 1).
Средняя за период мощность, т.е. активная мощность, резистивного элемента
,
где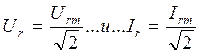 
(14)
действующие значения напряжения и тока.
Мгновенная мощность индуктивного элемента изменяется по синусоидальному закону
с частотой 
(рис 2).
Среднее значение мощности за период для индуктивного элемента равна нулю:
. (15)
Синусоидальный ток в индуктивном элементе не совершает работы. При положительном значении мощности она потребляется индуктивностью, при отрицательном – отдается обратно источнику. Такое энергетическое состояние цепи характеризуется так называемой реактивной мощностью, равной максимальной мгновенной мощности
. (16)
Хотя размерности активной и реактивной индуктивной мощностей совпадают, для измерения реактивной индуктивной мощности выбрана своя единица - Вар.
В емкостном элементе, также как и в индуктивном, мгновенная мощность - синусоидальная величина:
, (17)
частота которой вдвое больше частоты тока (рис 3). Здесь ток iL также не совершает работы. Энергетический режим принято определять реактивной емкостной мощностью
. (18)
Мощности 
и 
сдвинуты по фазе относительно друг друга на 1800, поэтому эти элементы, соединенные в электрическую цепь, могут обмениваться энергией не только с источником, но и друг с другом.
Полная мощность определяет эксплуатационные возможности многих электротехнических устройств. Связь между активной, реактивной и полной мощностью видно из выражения
. (19)
Коэффициент мощности 
является важным энергетическим показателем, который определяется отношением
, (20)
откуда нетрудно определить угол сдвига фаз между током и напряжением на данном элементе 
.
ИСТОЧНИКИ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ
СИНУСОИДАЛЬНОГО ТОКА
Промышленными источникамисинусоидального тока являются электромеханические генераторы, в которых механическая энергия паровых и гидравлических турбин преобразуется в электрическую.
Принципиальная конструкция простейшего электромеханического генератора содержит неподвижный, плоский разомкнутый виток с выводами а и в и постоянный магнит, который вращается с постоянной частотой f, т.е. с постоянной угловой частотой 
, внутри витка.
Основная единица частоты в системе СИ – герц (Гц). Величина обратная частоте называется периодом 
, измеряется в секундах (с).
Пусть магнитный поток постоянного магнита равен Фm. Из пространственного расположения магнитного потока следует, что мгновенное значение составляющей магнитного потока, пронизывающей виток, т.е. направленной вдоль оси х, равно
(1)
где Фm – максимальное значение (амплитуда) магнитного потока, пронизывающего виток; a - начальный (т.е. в момент t=0 принятый за начало отсчета времени) угол пространственного расположения постоянного магнита относительно оси х; jФ - начальная фаза магнитного потока, 
;
- фаза магнитного потока. Здесь и в дальнейшем начальная фаза определяет значение синусоидальной величины в момент времени t = 0.
Согласно закону электромагнитной индукции при изменении потокосцепления витка в нем индуцируется ЭДС
Подставляя сюда (1), имеем
где 
- амплитуда ЭДС, 
- начальная фаза ЭДС, 
Синусоидальные величины принято изображать графически в виде зависимости 
. Поэтому начальная фаза определяет смещение синусоидальной величины относительно начала координат, т.е. от 
.
Если начальная фаза >0, то начало синусоидальной величины сдвинуто влево, если <0, то – вправо от начала координат.
Если к выводам «а» и «в» генератора подключить резистор, то в полученной цепи возникнет синусоидальный ток i.
Максимальное, среднее и действующее значения
синусоидальных напряжений и токов
В линейной цепи при действии синусоидально изменяющейся ЭДС напряжения и токи также синусоидальны
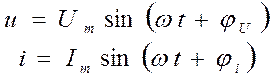
где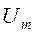 
и 
- максимальные значения (амплитуды) напряжения и тока.
Средним значением синусоидальной величины (ЭДС, тока, напряжения) считают ее среднее значение за положительный полупериод, совпадающее со средним значением по модулю.
Средние значения тока, ЭДС и напряжения определяются по следующим выражениям:
Синусоидальный ток в резистивном элементе с сопротивлением r вызывает нагрев этого элемента из-за выделения тепловой энергии. Такую же тепловую энергию в этом же резистивном элементе можно получить при некотором постоянном токе.
Определение посредством такого сравнения значения постоянного тока называется действующим значением синусоидального тока.
Для синусоидального тока можно определить действующее значение через амплитудное:
Аналогично для любой другой синусоидальной величины (ЭДС, магнитного потока, напряжения, заряда) действующее значение меньше его амплитуды в корень из двух раз.
Действующее значение выбрано в качестве основной характеристики синусоидального тока потому, что в большом числе случаев действие тока пропорционально квадрату этого значения, например тепловое действие и сила взаимодействия прямого и обратного проводов двухпроводной линии.
При расчете изоляции важно учесть, что дважды за период мгновенное значение синусоидального напряжения больше действующего в корень из двух раз. Следовательно, изоляция в установке синусоидального тока находится в менее благоприятных условиях, чем изоляция в аналогичной установке постоянного тока.