Классификация состояний в неразложимой цепи

Классификация по асимптотическим свойствам вероятностей Р_jj(n)

а) невозвратные

б) возвратные нулевые

в) ненулевые

Классификация по арифметическим свойствам вероятностей Р_jj(n)

а) периодические

б) непериодические

 

Упражнения

 

В задачах 22–24 выяснить, будет ли цепь с матрицей вероятностей перехода за один шаг P периодической. Для периодических цепей указать период.

22. P =

23. P =

24. P =

В задачах 25–27 указать возвратные и невозвратные состояния.

25. P = .

26. P =

27. P =

 

4. Симметричное случайное блуждание

Пример 1. Рассмотрим одномерное случайное блуждание по целочисленной решетке (). Симметричное одномерное случайное блуждание (р = q = ) возвратно.

Доказательство.

P₀₀(2n+1) = 0, P₀₀(2n) = , n = 0,2,…

По формуле Стирлинга, n! nⁿe^–n , P₀₀(2n) .

Состояние возвратно при p = q = , т.к. .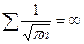

Пример 2. Рассмотрим двумерное случайное блуждание по целочисленной решетке на плоскости. Симметричное двумерное случайное блуждание возвратно.

Доказательство.

Рассмотрим все траектории: из 0 в 0, состоящие из i перемещений вправо, i влево, j вверх и j вниз, 2i+2j=2n. Вероятность за один шаг переместиться в любом из четырех направлений равна .

(*) P₀₀(2n) = , n = 1,2,3,…; P₀₀(2n+1) = 0, n = 0,1,…

Умножим числитель и знаменатель в (*) на (n!)² , получим

P₀₀(2n) = , но ; докажем это.

Рассмотрим равенство (1+x)²ⁿ = (1+x)ⁿ (1+x)ⁿ и приравняем коэффициенты при xⁿ: , но Т.о., P₀₀(2n) = и по формуле Стирлинга

(n! ) тогда

P₀₀(2n) ,

, состояние возвратно.

Пример 3. Симметричное случайное блуждание по трём измерениям невозвратно.

Доказательство.

P₀₀(2n+1) = 0, n = 0, 1, …, P₀₀(2n) = .

Умножим числитель и знаменатель на (n!)², получим:

P₀₀(2n) = .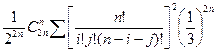

Если то P₀₀(2n) ≤ .

Мы использовали то, что

= 1.

Max C_n достигается (при больших n) при i = j ~ , тогда С_n ~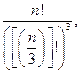

P₀₀(2n) ≤ Применим, как выше, формулу Стирлинга (сделать это самостоятельно!) и получим, что P₀₀(2n)

Тогда < => состояние невозвратное.

Теорема 2. Симметричное случайное блуждание возвратно в пространствах одного и двух измерений и невозвратно в пространстве трёх и более измерений.

Лемма. Одномерное случайное блуждание образует возвратную цепь Маркова тогда и только тогда, когда р = q = .

Доказательство леммы.

В примере 1 были получены вероятности P₀₀(2n+1) = 0, P₀₀(2n) = . При р = q = , P₀₀(2n) = , .

При p ≠ q, , т.к. (4pq)ⁿ = ⁿ,  < 1, а ряд по признаку Даламбера.

Доказательство теоремы.

Для одномерного случая (k=1) утверждение теоремы доказано в лемме. Рассмотрим теперь двумерный случай (k=2). Блуждание можно представить в виде суммы двух независимых компонент:

x(n) = (x₁(n), 0)+(0, x₂(n)), где x_i(n)– одномерные последовательности.

Тогда x(n+1) = x(n) + ξ_n, где ξ_n принимает четыре значения: ().

P₀₀(2n) = P(x(2n) = (0,0)/x(0) = (0,0)) = P(x₁(2n) = 0/x₁(0) = 0)∙P(x₂(2n) = 0/x₂(0) = 0) = , состояние возвратно.

При k = 3: P₀₀(2n) = O , , состояние невозвратно.

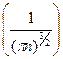При k > 3: P₀₀(2n) = O , состояние невозвратно.

Несимметричное случайное блуждание (при p ≠ q) невозвратно для любого k (т.к. (4pq)ⁿ = ⁿ,  < 1, ).

Упражнения

 

Шары.

N черных и N белых шаров размещены в двух урнах по N шаров в каждой. Число черных шаров в первой урне определяет состояние системы. На каждом шагу случайно выбирается по одному шару из каждой урны, и эти выбранные шары меняются местами.

а) найти все вероятности перехода за один шаг,

б) классифицировать состояния.

Прямая.

Точка движется по прямой и в течение каждой очередной секунды движения может или сместиться на единицу расстояния или остаться на месте. Даны: 1) вероятность p смещения для первой секунды; 2) вероятность а (а = const) смещения для любой рассматриваемой секунды, если известно, что в течение предыдущей секунды точка смещалась, 3) вероятность b (b = const) смещения для любой рассматриваемой секунды, если известно, что в течение предыдущей секунды точка оставалась на месте. Найти вероятность смещения точки в течение (n+1)–й секунды.

Плоскость.

Точка движется по плоскости и в течение секунды может сместиться или на единицу расстояния по горизонтали, и на единицу расстояния по вертикали, или пройти диагональ единичного квадрата (смещение на единицу по горизонтали и единицу по вертикали), или остаться на месте. Вероятность горизонтального и вертикального смещений одинакова и для любой секунды (кроме первой) равна: 1) а, если в предыдущую секунду произошли оба смещения; 2) b, если в предыдущую секунду произошло только одно смещение по горизонтали или по вертикали: 3) c, если в предыдущую секунду точка оставалась на месте. Составить уравнение цепи Маркова для определения вероятностей горизонтального (вертикального) смещения точки в течение (n+1)–й секунды.

31. Серия успехов.

Пусть имеется последовательность независимых испытаний, в каждом из которых вероятность появления события А равна p, (0<p <1), непоявление события А обозначим через В (В = не А). Под изучаемой системой будем понимать всевозможные комбинации из А и B в сериях последовательных испытаний. Будем считать, что система в момент t находится в состоянии E_k (k = 0, 1, 2,...), если в испытаниях с номерами t, t –1,t – 2,..., t –k+1 появилось А, а в испытании с номером t – k появилось В. Система в данный момент t находится в состоянии Е₀, если исходом испытания с номером t является В.

В начальный момент 0 система находилась в состоянии Е₀.

Написать матрицу переходных вероятностей, вычислить матрицу перехода через n шагов.

Частицы.

В некоторой области пространства имеются однородные частицы. Состояние изучаемой системы определяется числом частиц в данной области. В течение промежутка времени длиной 1 каждая частица независимо от других может покинуть эту область с постоянной вероятностью q. Кроме того, в области может появиться в течение единицы времени r

новых частиц (r = 0, 1, 2,,,,) с вероятностью, определяемой законом Пуассона с параметром λ.

Найти матрицу переходных вероятностей.

5. Теорема солидарности

Теорема 3. В неразложимой Марковской цепи все состояния принадлежат одному типу: если хоть одно возвратно, то и все возвратны; если хоть одно нулевое, то и все нулевые; если хоть одно периодическое с периодом d, то и все периодичны с периодом d.

Доказательство: Пусть _k, _j – два разных состояния. Существуют такие числа s, t, что P_kj(s) > 0, P_jk(t) > 0. По формуле полной вероятности

P_kk(s + t + n) = P_kk(s+n+t) =

P_kk(s + t + n) ≥ P_kj(s)P_jj(n)P_jk(t) (1)

Аналогично, P_jj (s + t + n) = P_jj(t + n + s) ≥ P_jk(t)P_kk(n)P_kj(s) (2)

 

Обозначим P_kj(s) = A, P_jk(t) = B. Тогда

P_kk(s + t + n) ≥ ABP_jj(n) (1^/)

P_jj(t + n + s) ≥ ABP_kk(n) (2^/)

P_jj(n) ≤ P_kk(s + t + n) (1^//).

Обозначим s+t+n = u, тогда n = u–s–t.

P_jj(u) ≥ ABP_kk(u – s – t) (2^//)

Равенство (2^//) справедливо для любых u, не меньших n, поэтому справедливо и для n:

P_jj(n) ≥ ABP_kk(n – s – t) (2^///)

Объединим (1^//) и (2^///):

ABP_kk(n–s–t) ≤ P_jj(n) ≤ P_kk(n+s+t).

ABP_kk(n – s – t) ≤ P_jj(n) ≤ P_kk(n + s + t).

1) Пусть _k– нулевое, тогда , но тогда и , следовательно, _j – нулевое.

2) Пусть _k– возвратное, т.е.

_j – возвратное.

3) Пусть _k – периодичное состояние с периодом d_k, т.е. P_kk(u) > 0, следовательно, существует такое b, что u = bd_k.

P_kk(t + s) ³ P_kj(s)P_jk(t) = AB > 0 Þ t + s = ad_k.

Рассмотрим _j. Если для некоторого n P_jj(n) > 0, то P_kk(n + t + s) > 0 Þ n + t + s = cd_k.

n + ad_k = cd_k Þ n = (c – a)d_k Þ цепь периодическая с периодом d_j, где d_j ≥ d_k. Аналогично можно показать, что d_k ≥ d_j Þ d_k = d_j ¨

Если состояния цепи Маркова периодичны с периодом d > 1, то цепь называется периодической. Изучение периодических цепей в значимой мере может быть сведено к изучению непериодических.

Теорема 4. Если цепь Маркова периодическая с периодом d, то множество состояний разбивается на d подклассов y₀, y₁,..., y_d–1 таких, что с вероятностью 1 за один шаг система переходит из класса y_n в y_n+1, из класса y_d–1 система переходит в y₀.

Доказательство: Выберем любое состояние, например ₁. Построим с помощью этого состояния подклассы y₀, y₁,..., y_d–1 следующим образом: _i Î y_a, 0 ≤  ≤ d–1, если существует целое число k > 0 такое, что P_1i(kd + a) >0. Покажем, что никакое состояние не может принадлежать сразу двум подклассам. Для этого достаточно доказать, что если _i Î y_a и для некоторого s P_1i(s) > 0, то s = a(mod d). Действительно, существует

t₁ > 0 такое, что P_i1(t₁) > 0. Тогда P₁₁(kd + a + t₁) ³ P_1i(kd+a)P_i1(t₁) > 0. Кроме этого, P₁₁(s + t₁) ³ P_1i(s)P_i1(t₁) > 0. Значит, kd + a + t₁ = ad и s + t₁ = bd Þ

kd + a + bd – s = ad; a = s + d(a – b – k) Þ a = s(mod d).

Т.к. из состояния ₁ можно с положительной вероятностью попасть в любое

_i, то содержит все множество состояний. Докажем теперь, что система из y_a за один шаг с вероятностью 1 переходит в y_a+1 (+1 понимается по mod d). Для этого надо показать, что для _I Î y_a . Достаточно получить, что P_ij = 0, если _iÎy_a, _jÏy_a+1. От противного, пусть _iÎy_a, _jÏy_a+1 , Pij > 0. Тогда P_1j(kd+a+1) ³ P_1i(kd+a)P_ij(1) > 0, так как P_ij(1) = P_ij, но тогда _jÎy_a+1 – противоречие. ¨

Из теоремы видно, что матрица периодической цепи будет иметь вид

Из периодической цепи Маркова с периодом d можно образовать d новых цепей Маркова. Состояниями –ой цепи будут состояния из подкласса y_a. Вероятности перехода задаются равенствами . В силу только что доказанной теоремы . Новая цепь уже не будет иметь подклассов.

Упражнения

 

33. Доказать, что в неразложимой конечной цепи Маркова не может быть нулевых состояний.

34. Доказать, что в неразложимой конечной цепи Маркова не может быть невозвратных состояний.

35. Могут ли все состояния цепи Маркова со счетным числом состояний быть невозвратными?

36. Доказать, что для конечной цепи Маркова состояние возвратно тогда и только тогда, когда оно существенно.

37. Доказать, что, если в цепи Маркова состояние ε_j возвратно, то система с вероятностью 1 за бесконечное число шагов бесконечно много раз возвратится в ε_j. Если состояние ε_j невозвратно, то система с вероятностью 1 за бесконечное число шагов лишь конечное число раз возвратится в ε_j. Другими словами, после некоторого конечного числа шагов система никогда больше не возвратится в ε_j.

38. Пусть ξ_t – номер состояния в цепи Маркова в момент времени t; P(ξ₀ = 1) = 1,

матрица переходных вероятностей имеет вид .

Положим

Показать, что последовательность η_t является цепью Маркова, найти ее матрицу вероятностей перехода.

39 – 41. Пустьξ₁, ξ_2,… – независимые случайные величины, P(ξ_t = 1) = 1 – P(ξ_t = –1) = p.

Является ли цепью Маркова последовательность η_t, если:

39. η_t = ξ_t∙ ξ_t+1.

40. η_t = ξ₁∙ ξ₂∙… ∙ξ_t.

41. η_t = φ(ξ_t,ξ_t+1), где φ(–1, –1) = 1, φ(–1, 1) = 2, φ(1, –1) = 3, φ(1, 1) = 4.

6. Эргодичность и стационарные распределения

Определение 11. С остояние ε_j, для которого существует , не зависящий от i, называется эргодическим.

Замечание. Позднее будет показано, что не зависящий от i существует для любого возвратного состояния ε_j, не являющегося ни нулевым, ни периодическим. Таким образом, термин «эргодическое состояние» – это синоним для «возвратное, не нулевое, не периодическое состояние».

Смысл эргодичности. Существуют вероятности попадания системы в состояние ε_j через большой промежуток времени, причем они не зависят от начального состояния системы.

Определение 12. Цепь Маркова называется эргодическо й, если для любых i, j существует (все состояния эргодические).

Определение 13. Распределение вероятностей {a_k} называется стационарным распределением цепи Маркова, если для любого n справедливо: (n).

Пример 4. Пусть дана однородная цепь Маркова с матрицей переходных вероятностей P= Стационарным распределением для него является (a₁, a₂) = (2/3, 1/3). Проверим, что (1).

(2/3, 1/3) ∙

Это верно и для n = 2, 3, 4:

P² =

(2/3, 1/3) ∙ =

P³ =

(2/3, 1/3) ∙ =

P⁴ =

(2/3, 1/3) ∙ =

Упражнение. Найдите общий вид матрицы P(n) = Pⁿ = и убедитесь в стационарности распределения. Найдите пределы элементов матрицы Pⁿ и убедитесь, что

Замечание. Если для однородной цепи Маркова справедливо: , то {a_k} – стационарное распределение.

Пример 5. Пусть дана однородная эргодическая цепь Маркова с матрицей переходных вероятностей

P=

Найти стационарное распределение.

Решение. Ищем решениеуравнения(a₁, a₂)∙P = (a₁, a₂).

(a₁, a₂)∙ (a₁, a₂),

1/3a₁ + 1/4 a₂ = a₁, 2/3a₁ + 3/4 a₂ = a₂, а также a₁ + a₂ = 1.

Решая систему, находим: a₁ = 3/11, a₂ = 8/11.

 

Выясним общие условия существования стационарного распределения.

Теорема 5. Неразложимая непериодическая цепь Маркова принадлежит одному из следующих классов:

а) или все состояния невозвратные, или все нулевые. В этом случае и не существует стационарного распределения;

б) или все состояния эргодические, т.е., . В этом случае {U_k}– стационарное распределение, и не существует никаких других стационарных распределений.

Доказательство: Рассмотрим случай б). Заметим, что поэтому «обрезанная» сумма не превышает 1, и это верно и в пределе. Так как , N получаем, что U₁+…+U_N ≤ 1.

Далее, для любых j, k, m, n справедливо: . Положим n = 1: . Если мы сужаем множество индексов в правой части, то справедливо неравенство:

, где А = {1, 2,…, N}. Пусть теперь m → ∞. По теореме о мажорируемой сходимости можно переходить к пределу. Поскольку , , то , что верно для любого А, то есть, для любого N, и в пределе при N→ ∞ получим .

Докажем, что имеет место равенство.

Если для каких–то k , то, просуммировав, получим: , однако они равны, так как состоят из одних и тех же слагаемых. Т.о.,

Следовательно, это стационарное распределение.

Докажем единственность. Пусть {V_k} удовлетворяет (*), . Умножим на p_kj = p_kj(1).: , просуммируем по k. . Но =V_j, а . Получили: . Опять умножим обе части на p_jk= p_jk(1), , просуммируем по j. , 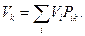(3) и т.д. по индукции. Пусть покажем, что , просуммируем по k. Заменим индекс j на k, получим:

Пусть n → ∞, с учетом того, что в пределе получаем V_k = (V₁+…)U_k = U_k (так как сумма вероятностей стационарного распределения равна единице).

Таким образом, стационарное распределение {V_k} совпадает с {U_k}, то есть, стационарное распределение единственно.

В случае а), если все состояния или невозвратные, или нулевые, предположим, что распределение {V_k} стационарно. Тогда, как показано выше, имеет место уравнение . Но противоречие. Поэтому стационарное распределение для неразложимой цепи может существовать только в эргодическом случае.