Ход занятия.
I. Организационный момент
Проверка подготовки группы к уроку
Работа с классным журналом.
II. Постановка темы и задач занятия
Сегодня мы с вами рассмотрим определение пирамиды, ее основных элементов и формулы вычисления площади ее поверхности.
III. Повторение изученного
Беседа по вопросам:
1. Призма имеет п граней. Какой многоугольник лежит в ее основании?
2. Является ли призма прямой, если две ее смежные боковые грани перпендикулярны к плоскости основания?
3. В какой призме боковые ребра параллельны ее высоте?
4. Является ли призма правильной, если все ее ребра равны друг другу?
5. Может ли высота одной из боковых граней наклонной призмы являться и высотой призмы?
6. Существует ли призма, у которой: а) боковое ребро перпендикулярно только одному ребру основания; б) только одна боковая грань перпендикулярна к основанию?
7. Правильная треугольная призма разбивается плоскостью, проходящей через средние линии оснований, на две призмы. Как относятся площади боковых поверхностей этих призм?
8. На какие многогранники рассекается треугольная призма плоскостью, проходящей через вершину верхнего основания и противолежащую ей сторону нижнего основания?
9. Докажите, что: а) у прямой призмы все боковые грани — прямоугольники; б) у правильной призмы все боковые грани — равные прямоугольники.
Проверка домашнего задания.
Глава 3, § 1, п. 30, № 224, с. 67 – 68
224. Диагональ правильной четырехугольной призмы наклонена к плоскости основания под углом 60°. Найдите площадь сечения, проходящего через сторону нижнего основания и противолежащую сторону верхнего основания, если диагональ основания равна 4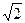 
см.
IV. Изучение нового
Пирамида. Рассмотрим многоугольник А1А2...Ап точку Р, не лежащую в плоскости этого многоугольника. Соединив точку Р отрезками с вершинами многоугольника, получим n треугольников (рис. 73):
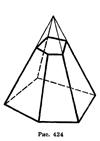
Многогранник, составленный из n -угольника А1А2...Ап и n треугольников (1), называется пирамидой. Многоугольник А1А2...Ап называется основанием, а треугольники (1) — боковыми гранями пирамиды. Точка Р называется вершиной пирамиды, а отрезки PA1, PA2,..., РАп — ее боковыми ребрами. Пирамиду с основанием А1А2...Ап и вершиной Р обозначают так: РА1А2...Ап — и называют n -угольной пирамидой. На рисунках 3, 4 изображены четырехугольная и шестиугольная пирамиды. Ясно, что треугольная пирамида — это тетраэдр.
Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. На рисунке 1 отрезок РН — высота пирамиды.
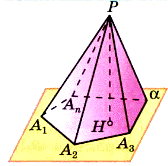
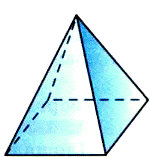
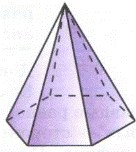
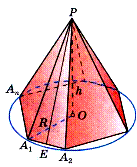
Рис. 1 Рис. 2 Рис. 3 Рис. 4
Правильная пирамида.
Пирамида называется правильной, если ее основание — правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой (рис. 4).
Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. На рисунке 4 отрезок РЕ — одна из апофем. Ясно, что все апофемы правильной пирамиды равны друг другу.
Площадью полной поверхности пирамиды называется сумма площадей всех ее граней (т. е. основания и боковых граней), а площадью боковой поверхности пирамиды — сумма площадей ее боковых граней.
Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Усеченная пирамида.
Возьмем произвольную пирамиду РА1А2...Ап и проведем секущую плоскость b, параллельную плоскости а основания пирамиды и пересекающую боковые ребра в точках В1, В2,..., Вп (рис. 5).
Плоскость b разбивает пирамиду на два многогранника. Многогранник, гранями которого являются n –угольники A1A 2... Ап и В1В2... Вп {нижнее и верхнее основания}, расположенные в параллельных плоскостях, и п четырехугольников (боковые грани), называется усеченной пирамидой. Отрезки А2В2,.... АnВп называются боковыми ребрами усеченной пирамиды.
Усеченную пирамиду с основаниями A1A 2... Ап и В1В2... Вп
обозначают так: A1A 2... Ап В1В2... Вп..
Рис. 5 Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усеченной пирамиды.
Боковые грани усеченной пирамиды — трапеции.
Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильной усеченной пирамиды — правильные многоугольники, а боковые грани — равнобедренные трапеции (докажите это). Высоты этих трапеций называются апофемами.
Теорема. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
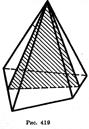
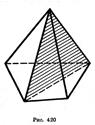
Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники (рис. 419). В частности, треугольниками являются диагональные сечения. Это сечения плоскостями, проходящими через два несоседних боковых ребра пирамиды (рис. 420).
Сечение пирамиды плоскостью с заданным следом g на плоскости основания строится так же, как и сечение призмы. Для построения сечения пирамиды плоскостью достаточно построить пересечения ее боковых граней с секущей плоскостью.
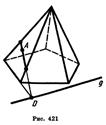
Если на грани, не параллельной следу g, известна какая-нибудь точка А принадлежащая сечению, то сначала строится пересечение следа g секущей плоскости с плоскостью этой грани — точка D на рисунке 421. Точка D соединяется с точкой А прямой. Тогда отрезок этой прямой, принадлежащий грани, есть пересечение этой грани с секущей плоскостью. Если точка А лежит на грани, параллельной следу g, то секущая плоскость пересекает эту грань по отрезку, параллельному прямой g. Переходя к соседней боковой грани, строят ее пересечение с секущей плоскостью и т. д. В итоге получается требуемое сечение пирамиды.
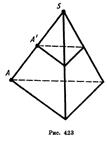
На рисунке 422 построено сечение четырехугольной пирамиды плоскостью, проходящей через сторону основания и точку А на одном из ее боковых ребер.
V. Закрепление изученного