Содержание
Охарактеризовать экспертные методы оценки качества
Перечислить требования к органам сертификации
3. В чем заключается принцип ограничения предельных контуров при построении систем допусков и посадок
4. Отклонения и допуски формы и расположения поверхностей
. Что является нарушением правил внутреннего распорядка
Задача
Список использованных источников
Охарактеризовать экспертные методы оценки качества
В соответствии с одним из основных принципов квалиметрии каждое свойство продукции, находящееся на любом уровне иерархической структуры её качества (дерева свойств), количественно определяется в полной мере двумя числовыми характеристиками: относительным показателем Kij и коэффициентом весомости Mij, где j - номер оцениваемого свойства (j=1,2,3,...,n), располагающегося на i-ом уровне иерархической структуры качества объекта (i=1,2,3,…,m). При использовании дифференциального метода оценки уровня качества продукции весомости отдельных свойств, определяющих её качество, не учитываются, и это является одним из недостатков данного метода. В случае же оценки уровня качества продукции комплексным методом целесообразно учитывать весомости отдельных свойств, определяющих её качество. Таким образом, возникает задача количественной оценки весомости учитываемых свойств продукции и определения их коэффициентов весомости Mij. Все используемые на практике методы решения этой задачи можно разделить на две группы: 1 - аналитеческие; 2 - экспертные. Причём, при разработке методик оценки уровня качества различных объектов предпочтение, как правило, отдают экспертным методам в силу их универсальности, простоты реализации, ''гибкости'' и достаточно высокой достоверности получаемых на их основе результатов оценки весомости свойств различных объектов.
Самым простым из всех экспертных методов оценки весомости свойств объектов является метод предпочтения. При использовании этого метода от каждого эксперта требуется пронумеровать весомости в порядке их предпочтения. При этом весомости наименее предпочитаемого свойства (наименее важного свойства) эксперт должен присвоить номер 1, следующему по важности свойству - номер 2 и т.д.. На основе полученных таким образом экспертных оценок рассчитываются коэффициенты весомости всех выделенных для оценки свойств с использованием следующего аналитического выражения:
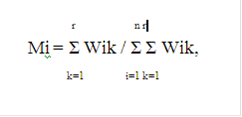
где Wik - место, на которое поставлено i-ое свойство с учётом его весомости k-ым экспертом;- количество экспертов, участвовавших в экспертизе;- количество оцениваемых свойств.
Весьма близок к рассмотренному методу, как по процедуре опроса экспертов, так и по обработке результатов экспертизы так называемый метод ранга. При реализации этого метода эксперты должны осуществить прямое оценивание важности каждого выделенного свойства по шкале относительной значимости в диапазоне значений оценок от 1 до 10. Причём, экспертам разрешено по этой шкале выставлять оцениваемым свойствам не только целые, но и дробные значения оценок, кроме того, одинаковые значения оценок одинаково значимым на их взгляд свойствам. Для определения искомых значений коэффициентов весомости оцениваемых свойств предлагается использовать при этом следующие формулы:

где Мik = Pik / Σ Pik, причём Pik - абсолютное значение оценки весомости i-ого свойства, определенное по10-балльной шкале k-ым экспертом.
Наиболее широкое распространение на практике получили методы попарного сопоставления (первый, второй метод попарного сопоставления, а также метод полного попарного сопоставления), которые по сравнению с другими экспертными методами оценки весомости свойств объектов характеризуются наиболее высоким уровнем достоверности получаемых результатов оценки.
При использовании первого метода попарного сопоставления каждый эксперт в качестве исходного материала получает специальную матрицу, в которой по горизонтали и по вертикали обозначены все сравниваемые свойства. Такую матрицу с примерами заполнения в наиболее общем виде можно представить следующим образом:
| Наименование свойства | № свойства | … | n | |||
| - | … | |||||
| - | … | |||||
| - | … | |||||
| … | … | … | … | - | ||
| n | ||||||
| Эксперт № ___ |
Анализируя данную матрицу, эксперт на пересечении столбцов и строк для каждой из пар сравниваемых свойств должен выставить оценку 1 или 0 в зависимости от определенной им важности (значимости) того или иного свойства (более важному свойству ставиться оценка 1 и соответственно менее важному из данной пары сравниваемых свойств - оценка 0). Для определения коэффициентов весомости выделенных свойств этим методом на основе полученных массивов (матриц) экспертных оценок используют следующие расчётные формулы:
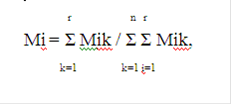
где Мik = fik /C, fik = Σ f(i/i’)k, здесь: fik - частота превалирования у k-ого эксперта весомости i-го свойства над весомостями всех остальных свойств; f(i/i’)k - оценка превалирования у k-ого эксперта весомости i-ого свойства над весомостью i’-ого свойства (принимает значения либо 0, либо 1 в зависимости от того, какое свойство считается более значимым); С - общее число возможных суждений или комбинаций, определяемое по формуле
=n(n-1)/2.
Используя второй метод попарного сопоставления, эксперты сравнивают пары свойств и определяют преимущество одного из них над другими не с помощью специальной матрицы, а просто анализируя свойства и подчёркивая предпочтительное свойство в каждой из представленных им комбинаций или пар свойств вида:
свойство 1 - свойство 2
свойство 7 - свойство 15
свойство 4 - свойство 1
и т.д.
При этом расчётные формулы для определения коэффициентов весомости оцениваемых свойств объектов используются те же, что и в предыдущем случае.
Метод полного попарного сопоставления принципиально отличается от первого и второго методов попарного сопоставления методикой проведения опроса экспертов, и его суть заключается в следующем:
Чтобы избежать возможных ошибок, связанных с тем, что какому-то i-ому свойству экспертами может отдаваться предпочтение с точки зрения его важности по сравнению со свойством i’ не потому, что оно действительно является более значимым, а потому, что при сравнении этих свойств по второму методу попарного сопоставления его случайно поставили первым в паре, сравнение предлагается производить не только в порядке ''свойство i - свойство i’ '', но и в обратном порядке ''свойство i’ - свойство i''.
Расчётные формулы при этом остаются прежними, за исключением формулы для определения параметра С, который в данном случае рассчитывается следующим образом:
=n(n-1).
Метод последовательных сопоставлений можно рассматривать как некоторую компиляцию метода предпочтения и метода ранга. При его реализации от экспертов требуется расположить весомости оцениваемых свойств в порядке их предпочтения (см. метод предпочтения). Наиболее важному свойству при этом присваивается коэффициент весомости М1=1.0, а всем остальным - в порядке убывания их значимости коэффициенты весомости в диапазоне от 1.0 до 0. Обработка результатов опроса экспертов в этом методе производится по формулам метода ранга. [4]