Рассмотрение числовых характеристик выборки необходимо начать с тех из них, которые характеризуют положение значений исследуемого признака на числовой оси, т. е. указывают некоторое среднее, ориентировочное значение, около которого группируются экспериментальные данные. К ним относятся среднее арифметическое, мода и медиана.
Среднее арифметическое равно сумме значений всех вариант выборки, деленное на объем выборки:
 .
.
Здесь п - объем выборки, а xi - варианты выборки.
Среднее арифметическое является наиболее важной характеристикой положения, поскольку при его определении используется вся имеющаяся информация о выборке. Для обозначения среднего арифметического используется та же буква, что и для вариант выборки, с той лишь разницей, что над буквой ставится черта - символ усреднения. В рассматриваемом случае исследуемый признак обозначен через X, его числовые значения - через хi, а среднее арифметическое имеет обозначение  .
.
Из определения среднего арифметического следует, что сумма отклонений выборочных значений признака от него равна нулю.
Вычислять среднее арифметическое исходя из его определения при большом объеме выборки становится затруднительным и можно применить следующий прием: воспользоваться результатами группировки и считать приближенно значения вариант в каждом интервале постоянными и равными срединному значению, которое выступает в роли «представителя» интервала. Число вариант в интервале равно частоте интервала, поэтому среднее арифметическое для сгруппированных данных будет выражаться следующей приближенной формулой:
 ,
,
где п - объем выборки;
k - число интервалов группировки;
ni - частоты интервалов;
xi - срединные значения интервалов.
Отметим, что платой за упрощение процесса вычислений является уменьшение их точности - точность вычислений по необработанным данным всегда выше, чем по обработанным. Исходя из этого, вычисление оценочных характеристик по первичным экспериментальным данным является предпочтительным.
Среднее арифметическое, вычисленное по результатам группировки, иногда называют взвешенным средним. Смысл такой формулировки заключается в том, что в формуле срединные значения суммируются с весами (коэффициентами), равными частотам попадания вариант в соответствующие интервалы группировки.
В качестве примера определим среднее арифметическое результатов в толкании ядра для экспериментальных данных из таблицы 1 и сгруппированных в таблице 4. Среднее арифметическое, определенное по необработанным экспериментальным данным, равно:
 14,5331 (м).
14,5331 (м).
При использовании для упрощения вычислений результатов проведенной группировки получаем:
 (4*13,375+8*14,045+10*14,715+5*15,385+2*16,055) / 29=14,55328 (м).
(4*13,375+8*14,045+10*14,715+5*15,385+2*16,055) / 29=14,55328 (м).
Полученные двумя способами средние арифметические различаются на две сотых, что превышает точность измерений экспериментальных данных.
Среди других характеристик положения наиболее важны мода и медиана. Они характеризуют величину варианты, занимающей определенное положение в статистической совокупности.
Модой случайной величины называется значение признака, встречающееся в выборке наиболее часто. Условимся использовать для обозначения моды символы Mo. Геометрически мода соответствует максимуму кривой эмпирического распределения (см. рис. 4).

Рис. 4. Мода
С точки зрения теории вероятностей модой случайной величины является ее наиболее вероятное значение.
Если распределение случайной величины имеет более одного максимума, то распределение называется “полимодальным” (см. рис. 5).

Рис. 5. Полимодальное распределение
На практике встречаются распределения, имеющие посередине не максимум, а минимум. Такие распределения принято называть “антимодальными” (см. рис. 6).

Рис. 6. Антимодальное распределение
Прежде чем приступить к вычислению значения моды в случае сгруппированных данных, необходимо определить модальный интервал. Модальным называется интервал группировки, содержащий наибольшее число вариант, т.е. имеющий максимальную частоту (частость).
Значение моды определяется по результатам группировки с помощью следующего соотношения:
 ,
,
где xMoH - нижняя граница модального интервала;
h -ширина интервала группировки;
пMo - частота модального интервала;
пМо- 1 - частота интервала, предшествующего модальному;
пмо +1 - частота интервала, следующего за модальным.
При проведении исследования может оказаться, что модальным оказывается первый или последний интервал группировки. В этом случае предыдущий или последующий интервал не существует и возникает вопрос о пути применения последней формулы. Если один из интервалов не существует, то при проведении вычисления моды значение частоты, соответствующее этому интервалу, следует принять равным нулю. Это интуитивно очевидно - раз нет интервала, то нет и вариант, относящихся к нему, потому и частота должна обращаться в нуль.
В рассматриваемом примере модальным является третий интервал, а значение моды равно:
 (м).
(м).
Часто для характеристики распределения применяется еще одна характеристика положения - медиана. Медианой называется такое значение признака, при которомполовина значений экспериментальных данных оказывается меньше его, а вторая половина — больше. Для обозначения медианы принято использовать символы Me. Геометрический смысл медианы – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам (см. рис. 7).

Рис. 7. Медиана
В случае несгруппированных данных для нахождения медианы необходимо ранжировать выборку, т. е. расположить данные в порядке их возрастания или убывания. Медианой будет являться значение признака, находящееся в середине ранжированного ряда. В ранжированной выборке, содержащей п членов, ранг RMe, т.е. порядковый номер, медианы равен:
 ,
,
а сама медиана совпадает с членом выборки, имеющим номер RMe. Описанное правило дает однозначный результат, если выборка содержит нечетное число членов.
Если же выборка содержит четное число членов, то медиана не может быть определена столь однозначно. Действительно, RMe оказывается дробным. В этом случае берут два члена выборки с номерами большим и меньшим RMe и считают медиану, равной их среднему значению.
Для определения медианы в случае сгруппированных данных необходимо найти медианный интервал. Интервал группировки, содержащий медиану, называется медианным. Медианным является интервал, в котором накопленная частота впервые окажется больше половины объема выборки (либо накопленная частость - больше 0,5). Значение медианы определяется по следующей формуле:
 ,
,
где хМе H - нижняя граница медианного интервала;
n - объем выборки;
h - ширина интервалов группировки;
NMe -1 - накопленная частота интервала, предшествующего медианному;
пMe - частота медианного интервала.
В рассматриваемом примере накопленная частота впервые превышает половину объема выборки (накопленная частость 0,5) в третьем интервале (см. таблицу 4), поэтому он и будет являться медианным. Само значение медианы равно:
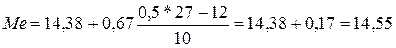 (м).
(м).
В рассматриваемом примере все характеристики положения различаются между собой. Это свидетельствует об асимметрии эмпирического распределения.
Значения среднего арифметического, моды и медианы совпадают только для симметричных одномодальных распределений. Напомним, что распределение является симметричным, если частости двух любых вариант, равно отстоящих в обе стороны от центра распределения, равны между собой. В таких случаях все характеристики положения равноправны, но предпочтение принято отдавать среднему арифметическому, поскольку оно опирается на всю имеющуюся информацию об изучаемой выборке. Чем сильнее форма распределения отклоняется от симметричной, тем большее различие наблюдается между значениями характеристик положения.
Значение медианы наиболее важно при исследовании сильно асимметричных эмпирических распределений. В этих случаях значительная часть значений признака оказывается больше, либо меньше среднего арифметического и последнее оказывается мало пригодным для описания положения центра распределения. Использование медианы, занимающей промежуточное значение между средней арифметической и модой, для характеристики центра распределения в описанной ситуации оказывается наиболее рациональным.