Пример. В соревнованиях по десятиборью участвовали 20 спортсменов. Результаты, показанные ими в метании диска и толкании ядра, приведены в таблице 6.
Таблица 6
Результаты метания диска и толкания ядра
| i | xi, метание диска (м) | yi, толкание ядра (м) |
| 40,9 | 13,84 | |
| 49,47 | 16,51 | |
| 45,44 | 15,83 | |
| 45,64 | 16,47 | |
| 43,76 | 13,40 | |
| 36,08 | 13,45 | |
| 33,92 | 13,88 | |
| 40,22 | 15,06 | |
| 39,47 | 14,68 | |
| 38,38 | 13,97 | |
| 38,68 | 13,70 | |
| 47,14 | 14,68 | |
| 36,47 | 12,85 | |
| 39,03 | 14,84 | |
| 46,3 | 15,65 | |
| 33,47 | 12,27 | |
| 44,97 | 14,97 | |
| 38,83 | 13,99 | |
| 42,68 | 15,03 | |
| 30,79 | 11,77 |
Исследовать, существует ли связь между результатами, показанными спортсменами в метании диска и результатами в толкании ядра. Сравнить вариацию двух обследуемых признаков. Если между двумя наборами данных существует связь, то построить линию регрессии.
Построим корреляционное поле, откладывая в прямоугольной системе координат по оси OX результаты, показанные в метании диска, а по оси OY – результаты, показанные в толкании ядра (см. рис. 16). Проведем огибающую для нанесенных точек.
Рис. 16. Корреляционное поле
Как видно из рассмотрения рисунка, огибающая имеет форму, близкую к эллипсу. Это позволяет предположить, что два набора данных связаны между собой линейной связью. Из рис. 6 видно, что увеличение значения результата, показанного в метании диска, приводит к увеличению значения результата, показанного в толкании ядра. Следовательно, предполагаемая связь является положительной. Поскольку связь линейная, а измерения значений исследуемых признаков производятся в шкале отношений, то для оценки ее силы можно воспользоваться коэффициентом корреляции Браве-Пирсона
.
Для определения коэффициента корреляции Браве-Пирсона воспользуемся вспомогательной таблицей. Построим таблицу, содержащую 8 столбцов и 23 строки (см. таблицу 6). В первом столбце разместим номера результатов (или спортсменов). Во втором и третьем столбцах – результаты, показанные спортсменами в метании диска (xi) и толкании ядра (yi).
Таблица 6
Определение коэффициента корреляции
| i | xi | yi |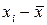 
| 
| 
| 
| 
|
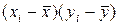
| 40,9 | 13,84 | 0,318 | -0,502 | -0,159636 | 0,101124 | 0,252004 | |
| 49,47 | 16,51 | 8,888 | 2,168 | 19,269184 | 78,996544 | 4,700224 | |
| 45,44 | 15,83 | 4,858 | 1,488 | 7,228704 | 23,600164 | 2,214144 | |
| 45,64 | 16,47 | 5,058 | 2,128 | 10,763424 | 25,583364 | 4,528384 | |
| 43,76 | 13,40 | 3,178 | -0,942 | -2,993676 | 10,099684 | 0,887364 | |
| 36,08 | 13,45 | -4,502 | -0,892 | 4,015784 | 20,268004 | 0,795664 | |
| 33,92 | 13,88 | -6,662 | -0,462 | 3,077844 | 44,382244 | 0,213444 | |
| 40,22 | 15,06 | -0,362 | 0,718 | -0,259916 | 0,131044 | 0,515524 | |
| 39,47 | 14,68 | -1,112 | 0,338 | -0,375856 | 1,236544 | 0,114244 | |
| 38,38 | 13,97 | -2,202 | -0,372 | 0,819144 | 4,848804 | 0,138384 | |
| 38,68 | 13,70 | -1,902 | -0,642 | 1,221084 | 3,617604 | 0,412164 | |
| 47,14 | 14,68 | 6,558 | 0,338 | 2,216604 | 43,007364 | 0,114244 | |
| 36,47 | 12,85 | -4,112 | -1,492 | 6,135104 | 16,908544 | 2,226064 | |
| 39,03 | 14,84 | -1,552 | 0,498 | -0,772896 | 2,408704 | 0,248004 | |
| 46,3 | 15,65 | 5,718 | 1,308 | 7,479144 | 32,695524 | 1,710864 | |
| 33,47 | 12,27 | -7,112 | -2,072 | 14,736064 | 50,580544 | 4,293184 | |
| 44,97 | 14,97 | 4,388 | 0,628 | 2,755664 | 19,254544 | 0,394384 | |
| 38,83 | 13,99 | -1,752 | -0,352 | 0,616704 | 3,069504 | 0,123904 | |
| 42,68 | 15,03 | 2,098 | 0,688 | 1,443424 | 4,401604 | 0,473344 | |
| 30,79 | 11,77 | -9,792 | -2,572 | 25,185024 | 95,883264 | 6,615184 | |
| Сумма | 811,64 | 286,84 | 102,40092 | 481,0747 | 30,97072 |
Вычислим суммы значений xi и yi и занесем их в соответствующие клетки строки «Сумма» (последняя строка таблицы) столбцов 2 и 3:
;
.
Рассчитаем средние значения признаков xi и yi:
;
.
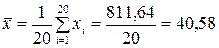В клетках столбца 4 вычислим разность значений результатов метания диска xi и их среднего значения 
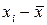: , а в клетках столбца 5 – аналогичную разность для толкания ядра 
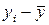. Суммы элементов этих столбцов должны быть равны нулю, поскольку сумма отклонений значений признака от среднего значения равна нулю.
В столбце 6 подсчитаем произведения отклонений двух исследуемых признаков от их средних значений (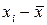)×()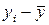. В столбце 7 вычислим квадраты отклонений результатов метания диска от среднего их значения – (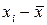)2, а в столбце 8 - квадраты отклонений результатов толкания ядра от их среднего значения – (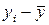)2. Подсчитаем соответствующие суммы и занесем результаты в последнюю строку таблицы:
;
;
.
Используя полученные значения вспомогательных сумм, вычислим значение коэффициента корреляции Браве-Пирсона:
.
Коэффициент корреляции лежит в интервале 
, поэтому можно сделать предположение о том, что между результатами, показанными спортсменами в метании диска, и результатами, показанными ими в толкании ядра, существует линейнаяположительная сильная статистическая взаимосвязь.
Коэффициент детерминации в рассматриваемом случае равен
.
Таким образом, 70% взаимосвязи между двумя наборами данных объясняется их взаимовлиянием. Остальная часть вариации обусловлена воздействием других неучтенных причин.
Для обоснования статистической значимости полученного коэффициента корреляции воспользуемся двусторонним критерием. Сформулируем статистические гипотезы. Н 0 – в генеральной совокупности корреляция отсутствует, а отличие от нуля выборочного коэффициента корреляции связано со случайностью выборки. Н 1 – в генеральной совокупности существует взаимосвязь между двумя исследуемыми признаками. Зададимся уровнем статистической значимости α =0,05. Соответствующее ему критическое значение коэффициента корреляции для объема выборки n =20 равно rкр =0,468 (см. таблицу 2 Приложения). Так как значение выборочного коэффициента корреляции превосходит значение критического для заданного уровня значимости, то делаем вывод о статистической значимости коэффициента корреляции на уровне значимости 0,05. Между результатами, показанными спортсменами в метании диска, и результатами, показанными ими в толкании ядра, существует значимая положительная взаимосвязь.
Обоснуем статистическую значимость коэффициента корреляции иным способом. Он используется тогда, когда таблицы критических значений коэффициента корреляции оказались по каким-либо причинам недоступными. В том случае для проверки статистической значимости применяется t -критерий Стьюдента, таблицы критических значений которого гораздо доступнее. Сами формулировки статистических гипотез Н 0 и Н 1 остаются без изменений. Вычислим эмпирическое значение t -критерия 
:
.
Сопоставим полученное значение с критическим значением критерия 
для числа степеней свободы 
и уровня значимости α =0,05. Критическое значение определяется с помощью специальных таблиц (см. таблицу 1 Приложения). В рассматриваемом случае оно равно =2,101. Поскольку эмпирическое значение критерия оказалось больше критического, то можно сделать вывод о том, что на уровне значимости 0,05 коэффициент корреляции является статистически значимым.
Для сравнения вариативности исследуемых признаков вычислим коэффициенты вариации. Предварительно, использую значения сумм столбцов 7 и 8 таблицы 3, необходимо вычислить дисперсии и стандартные отклонения:
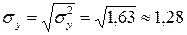
Подсчитаем коэффициенты вариации двух признаков:
;
.
Поскольку коэффициент вариации у результатов в метании диска больше, чем у результатов в толкании ядра, то этот признак варьирует сильнее. Следует отметить, что в рассматриваемом случае различия в варьировании признаков не велики.
Определим значения коэффициентов регрессии. Для этого воспользуемся вспомогательной таблицей 7.
Таблица 7
Определение коэффициентов регрессии
| i | xi | y i | xi 2 | xiyi | yi 2 |
| 40,9 | 13,84 | 1672,81 | 566,056 | 191,5456 | |
| 49,47 | 16,51 | 2447,2809 | 816,7497 | 272,5801 | |
| 45,44 | 15,83 | 2064,7936 | 719,3152 | 250,5889 | |
| 45,64 | 16,47 | 2083,0096 | 751,6908 | 271,2609 | |
| 43,76 | 13,40 | 1914,9376 | 586,384 | 179,56 | |
| 36,08 | 13,45 | 1301,7664 | 485,276 | 180,9025 | |
| 33,92 | 13,88 | 1150,5664 | 470,8096 | 192,6544 | |
| 40,22 | 15,06 | 1617,6484 | 605,7132 | 226,8036 | |
| 39,47 | 14,68 | 1557,8809 | 579,4196 | 215,5024 | |
| 38,38 | 13,97 | 1473,0244 | 536,1686 | 195,1609 | |
| 38,68 | 13,70 | 1496,1424 | 529,916 | 187,69 | |
| 47,14 | 14,68 | 2222,1796 | 692,0152 | 215,5024 | |
| 36,47 | 12,85 | 1330,0609 | 468,6395 | 165,1225 | |
| 39,03 | 14,84 | 1523,3409 | 579,2052 | 220,2256 | |
| 46,3 | 15,65 | 2143,69 | 724,595 | 244,9225 | |
| 33,47 | 12,27 | 1120,2409 | 410,6769 | 150,5529 | |
| 44,97 | 14,97 | 2022,3009 | 673,2009 | 224,1009 | |
| 38,83 | 13,99 | 1507,7689 | 543,2317 | 195,7201 | |
| 42,68 | 15,03 | 1821,5824 | 641,4804 | 225,9009 | |
| 30,79 | 11,77 | 948,0241 | 362,3983 | 138,5329 | |
| Сумма | 811,64 | 286,84 | 33419,0492 | 11742,9418 | 4144,8300 |
Первые три столбца совпадают с соответствующими столбцами таблицы 6. В столбце 4 таблицы 7 вычислим квадраты значений результатов метания диска 
, в столбце 5 произведения двух исследуемых признаков 
. В последней строке таблицы подсчитаем соответствующие суммы:
;
.
Вычислим коэффициент регрессии:
;
.
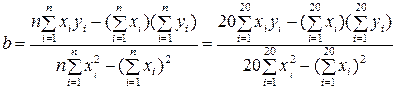Рассчитаем значение свободного члена уравнения регрессии
.
Таким образом, уравнение регрессии имеет вид:
.
Определим стандартную ошибку предсказания. Для этого в столбце 6 таблицы 3 вычислим квадраты значений результатов толкания ядра 
и занесем их сумму в последнюю строку:
.
Используя полученные результаты, вычислим стандартную ошибку предсказания:
.
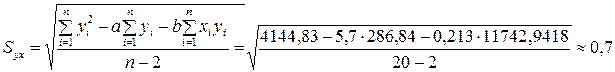Стандартная ошибка предсказания является характеристикой точности предсказания значений случайной величины y по известным значениям случайной величины x. Зона, ограниченная двумя прямыми, отстоящими от регрессионной прямой на расстояние ±0.7, является областью, в которую с вероятностью 0,7 попадают экспериментальные значения yi. Это означает, что приблизительно 70% всех значений yi находятся в этой области.
Проверим статистическую значимость полученного коэффициента регрессии. Сформулируем статистические гипотезы. Н0 – для рассматриваемой генеральной совокупности нет статистически значимого коэффициента регрессии. Н1 – полученный коэффициента регрессии является статистически значимым. Нулевая гипотеза проверяется с помощью t -критерия Стьюдента, эмпирическое значение которого вычисляется с помощью соотношения
Зададимся уровнем статистической значимости α =0,05. Соответствующее ему критическое значение для объема выборки n =20 и числа степеней ν = n -2=20-2=18 равно tкр =2,101 (см. таблицу 1 Приложения). Сравним эмпирическое значение t -критерия с критическим для выбранного уровня значимости. tэмп > tкр (tэмп >2,101), поэтому коэффициент регрессии b =0,213 является статистически значимым на уровне статистической значимости α =0,05.
Рассмотрим исследование взаимосвязи признаков с помощью коэффициента ранговой корреляции Спирмена.
Пример. В ходе тренировок группа спортсменов из 20 человек выполняют упражнения «подъем-разгибом» и «отмах в стойку». Результаты, зафиксированные при выполнении этих упражнений, приведены в таблице 8. Число выполнений упражнения «подъем-разгибом» каждым спортсменом приведено во второй колонке таблицы 8 обозначено x. Число выполнений упражнения «отмах в стойку» приведено в третьей колонке таблицы 8 и обозначено y. Исследовать зависимость между результатами выполнения упражнения «отмах в стойку» и результатами выполнения упражнения «подъем-разгибом».
Таблица 8
Вычисление коэффициента ранговой корреляции Спирмена.
| i | xi | yi | RXi | RYi | di | di 2 |
| 19,5 | 0,5 | 0,25 | ||||
| 12,5 | -2,5 | 6,25 | ||||
| 17,5 | -1,5 | 2,25 | ||||
| 15,5 | 2,5 | 6,25 | ||||
| 7,5 | 6,5 | 42,25 | ||||
| 1,5 | 3,5 | -2 | ||||
| 12,5 | -2,5 | 6,25 | ||||
| 7,5 | -0,5 | 0,25 | ||||
| 3,5 | 3,5 | |||||
| 1,5 | 3,5 | -2 | ||||
| 9,5 | -2,5 | 6,25 | ||||
| 15,5 | 0,5 | 0,25 | ||||
| 3,5 | 3,5 | |||||
| -1 | ||||||
| 12,5 | 9,5 | |||||
| 12,5 | 12,5 | |||||
| 19,5 | -0,5 | 0,25 | ||||
| 12,5 | -2,5 | 6,25 | ||||
| 17,5 | -1,5 | 2,25 | ||||
| Сумма |
Построим корреляционное поле, откладывая по оси X декартовой системы координат результаты выполнения упражнения «подъем-разгибом», а по оси Y – соответствующие им результаты выполнения упражнения «отмах в стойку» (см. рис. 17).
Рис. 17. Корреляционное поле
Как видно из рассмотрения рисунка, увеличение значения одного признака, приводит к увеличению значения второго. Это позволяет предположить, что два набора данных связаны положительной связью. Поскольку предполагаемая связь является монотонной, то для оценки ее силы можно воспользоваться коэффициентом ранговой корреляции Спирмена.
Вычислим ранги RXi и RYi значений исследуемых данных и занесем полученные результаты в 4 и 5 колонки таблицы 5.
Вычислим разности рангов RXi и RYi. Полученные данные обозначим di и занесем в шестую колонку. Сумма разностей равна нулю, что может быть использовано для проверки корректности вычислений.
Определим квадраты разностей рангов и суммируем их (
). Результат записываем в нижней строке таблицы.
Поскольку как среди результатов выполнения упражнения «подъем-разгибом», так и среди результатов выполнения упражнения «отмах в стойку» есть совпадающие значения, то вычислим поправочные коэффициенты. Среди результатов выполнения упражнения «подъем-разгибом» есть 7 групп совпадающих значений – по два раза встречается значения 10, 11, 16, 20 и по три раза встречается значения 13, 15, 18. Поэтому 
. Среди результатов выполнения упражнения «подъем-разгибом» по два раза встречаются значения 5, 6, 8, 9 и по четыре раза встречаются значения 3, 7, поэтому 
.
Подставим полученные значения в формулу для вычисления коэффициента корреляции Спирмена:
.
Определим статистическую достоверность полученного коэффициента корреляции. Для n =20 и уровня значимости α =0,05 критическое значение rs кр=0,45 (см. таблицу 3 Приложения).
Поскольку полученное значение r s превосходит критическое rs кр, то можно сделать вывод о статистически значимой положительной корреляции между результатами выполнения упражнения «отмах в стойку» и результатами выполнения упражнения «подъем-разгибом» (p <0,05).
Список литературы
Основная
1. Высшая математика и математическая статистика: учебное пособие для вузов/ под общ. ред. Г. И. Попова. – М.: Физическая культура, 2007. – 368 с.
2. Конюхов В.Г., Конюхова Г.П. Основы выборочного метода исследования. – М.: РИО РГУФК, 2005. – 43 с.
3. Основы математической статистики: учебное пособие для институтов физической культуры / под общ. ред. В. С. Иванова. – М.: Физкультура и спорт, 1990. – 176 с.
4. Селиванова Т.Г. Учебное пособие для студентов РГАФК. - М.: С.Принт, 1999. – 87с.
5. Спортивная метрология: учебник для институтов физической культуры / под ред. В. М. Зациорского. – М.: Физкультура и спорт, 1982. – 256 с.
Дополнительная
1. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1969. – 564с.
2. Гмурман В. Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 2006. – 479c.
3. Ивченко Г.И., Медведев Ю.Я. Математическая статистика. – М.: Высшая школа, 1994. – 328с.
4. Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика. - М.: Инфра-м, 1997. – 302с.
5. Селиванова Т.Г. Программа дисциплины «Математика» федерального компонента цикла ЕН ГОС по направлению 521900 «Физическая культура», по специальности 022300 «Физическая культура и спорт». – М.: РИО РГУФК, 2002.