


Далее сообщаем, что 1 дм3=1 л.
По программе Аргинской И.И. кроме этого выводят правило нахождения объёма куба и прямоугольного параллелепипеда: М4А ч.2 с.20-21 и 26.




Демидова М4 ч2 стр 4,5


Чекин М4 Ч1

Вопрос 5. Опишите методику знакомства учащихся с правилом нахождения объёма куба и прямоугольного параллелепипеда по программе И.И. Аргинской М4А ч.2 с.20 и 26. Составьте фрагмент урока по одной из этих страниц.
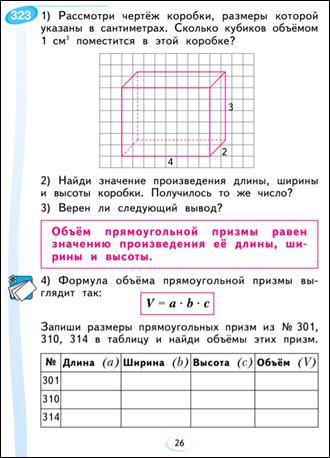
V = a ∙b ∙c Для вывода этого правила рассматриваем модель прямоугольного параллелепипеда. Можно её сложить из кубиков, принимая, что 1 кубик = 1 единице объёма, например 1 дм3.
Например, прямоугольный параллелепипед размером 3х4х5.
Уточняем: сколько всего кубиков в модели, т. е. сколько единиц измерения объёма, в этом прямоугольном параллелепипеде? Сначала подсчитываем, сколько кубиков потребовалось для одного уровня. Дети умеют находить S прямоугольника, следовательно, ответят 3∙4 =12. Уточняем, что обозначают числа 3 и 4? Это числовые значения длины и ширины. Таких уровней в нашем параллелепипеде 5, следовательно, всего 3∙4∙5 кубиков, где 5 – это числовое значение высоты, следовательно,
V параллелепипеда = произведению длины, ширины и высоты.
Учебник: УМК: «Система Занкова»; И.И. Аргинская, Е.И. Ивановская, С.Н. Кормишина; ч.2 с.26.
Темаурока: «Объём куба».
Цель:формирование представлений о измерении объёма,выведение формулы объёма куба.
Задачи урока:
1)Повторение изученного материала
2) Формирование представлений о измерении объёма;
3) Выведение формулы объёма куба.
Задачи: Образовательная задача. Обучить детей новому числу, его образованию.
воспитательная: - учить воспитанности, аккуратности.
развивающая:- развивать речь, мышление, совершенствовать
вычислительные навыки
Оборудование:
Дляучителя – конспект урока, учебник
Длядетей – учебник..
Ход урока:
1)Повторение изученного материала:
У: Ребята, кто может мне может сказать в чём измеряют объём?
Д:Объём измеряют кубическими миллиметрами, кубическими сантиметрами, кубическими дециметрами, кубическими метрами и даже кубическими километрами.
У: Ребята, правильно. А кто может показать на доске запись?
(Коля выходит к доске и записывает: 1 см3, 1дм3, 1м3, 1 км3).
2) Формирование представлений о измерении объёма:
У: Ребята, открываем страницу 26 упражнение 323 (2). На данном рисунке изображён чертёж коробки.Кто-то знает на какую геометрическую фигуру он похож?
Д: Нет или на куб.(Проблемная ситуация)
У: Ребята, кто мне скажет определения куба?
Д: Куб – это фигура, у которой все стороны равны!(Отвечает Катя)
У: Катя, неточный ответ. Кто может дать другое определение?
Д: Куб- многогранник,у которого все стороны равны.
У: Верно. Куб-это прямоугольный параллелепипед, у которого все три измерения равны. А на рисунке на 26 с. У фигуры все три измерения разные.
У: Чертёж коробки похож на прямоугольную призму. Чтобы ответить на вопрос задачи,давайте вспомним,как можно разложить 1см3?
Д: Аня отвечает: 1см3 = 1см*1см*1см
У:Верно. Ребята, смотрим все на рисунок. Что нам известно?
Д: Длина(4см), ширина (2см), высота(3см).
У: Правильно. Что же у нас получиться, если найти произведение длины, ширины и высоты коробки?
Д: Нужно длину умножить на ширину и на длину.
У: Что получиться, Федя?
Ф: 4*2*3=24
У: Ребята, поднимите руки,кто согласен с Федей.
Дети поднимают все руки.
У: Все – молодцы.
У: Сделаем вывод,что прямоугольной призмы равен значению произведения её длины, ширины, высоты! Ребята, это нужно запомнить.