Свойства определителей
1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число 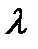 ,то ее определитель умножится на это число
,то ее определитель умножится на это число 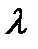 .
.
Замечание. За знак определителя можно выносить общий множитель любой строки (столбца) в отличие от матрицы, за знак которой можно выносить общий множитель всех элементов.
3. При транспонировании матрицы ее определитель не изменяется: 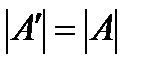 .
.
4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
5. Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.
6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0.
8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
9. Сумма произведений произвольных чисел 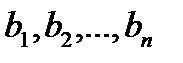 на алгебраические дополнения любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа
на алгебраические дополнения любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа 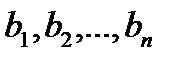 .
.
10. Определитель произведения двух квадратных матриц равен произведению их определителей: 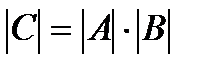 , где
, где 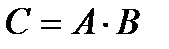 , а
, а 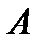 и
и 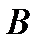 - матрицы
- матрицы 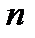 -го порядка.
-го порядка.
По теореме Лапласа определитель квадратной матрицы равен сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения.
Система может не иметь ни одного решения и тогда она называется несовместной, иначе, если она имеет хотя бы одно решение, то она называется совместной.
Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.
Следствия
Количество главных переменных системы равно рангу системы.
Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных
Доказательство.
1 Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А->А* не изменяют ранга.
2 Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора.
Линейное пространство – множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным ниже восьми аксиомам:
1 Ассоциативность суммы (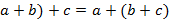
2 Коммутативность 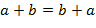
3 Существует нулевой вектор 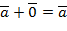
4 Существует противоположный элемент на множестве 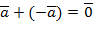
5 Умножение на число ассоциативно 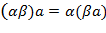
6 Умножение на вектор дистрибутивно относительно сложения чисел 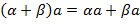
7 Умножение на число дистрибутивно относительно сложения элементов 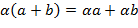
8 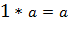 для любого вектора
для любого вектора 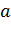
Следствия аксиом линейного пространства:
1 В линейном пространстве существует единственный нулевой вектор.
2 В линейном пространстве для любого вектора 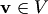 существует единственный противоположный вектор
существует единственный противоположный вектор 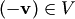 .
.
3 Произведение произвольного вектора пространства на число нуль равно нулевому вектору, т.е. 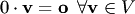 .
.
4 Произведение нулевого вектора на любое число равно нулевому вектору, т.е  для любого числа
для любого числа 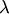 .
.
5 Вектор, противоположный данному вектору, равен произведению данного вектора на число (-1), т.е. 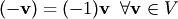 .
.
6 В выражениях вида 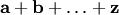 (сумма конечного числа векторов) или
(сумма конечного числа векторов) или 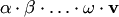 (произведение вектора на конечное число множителей) можно расставлять скобки в любом порядке, либо вообще не указывать.
(произведение вектора на конечное число множителей) можно расставлять скобки в любом порядке, либо вообще не указывать.
Теорема (критерий подпространства)
F является линейным подпространством 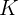 , если выполняются условия:
, если выполняются условия:
1. Если векторы 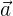 и
и 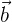 принадлежат
принадлежат 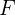 , то
, то 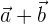 тоже принадлежат
тоже принадлежат 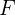 .
.
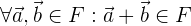 .
.
2. Если вектор 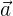 принадлежит
принадлежит 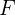 , то и
, то и 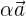 тоже принадлежит
тоже принадлежит 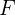 .
.
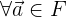 ,
, 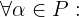
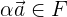
Доказательство. Если 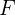 линейное подпространство
линейное подпространство 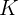 , значит
, значит 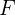 — линейное пространство, соответственно оно замкнуто относительно умножения и сложения векторов на скаляры .
— линейное пространство, соответственно оно замкнуто относительно умножения и сложения векторов на скаляры .
Система векторов линейно-независима, если линейная комбинация этих векторов равна нулевому вектору только при нулевых коэффициентах. То есть линейная комбинация имеет только одно нулевое решение.
Система векторов линейно-зависима, если существуют ненулевые коэффициенты, при которых линейная комбинация равна нулевому вектору.
Свойства линейно зависимых и независимых систем векторов:
Теорема 1. Если в системе векторов имеется нулевой вектор, то система линейно зависима.
Теорема 2. Если в системе векторов имеется линейно зависимая подсистема, то и вся система линейно зависима.
Теорема 3. Любая подсистема линейно независимой системы линейно независима.