На прошлых уроках мы с вами познакомились с электрическими цепями. Вспомним, что электрическая цепь — это совокупность устройств и элементов, предназначенных для протекания электрического тока.
Электрические цепи, с которыми мы сталкиваемся в повседневной жизни, чаще всего состоят не из одного потребителя электрического тока, а из нескольких, которые могут соединяться между собой различными способами. Поэтому возникают следующие вопросы: каким закономерностям подчиняются цепи, содержащие несколько потребителей? И как выгодно их соединять?
Одним из видов соединения является последовательное. Мы уже знакомились с ним, когда изучали электрические цепи. Так, в простейшей из них, последовательно соединены источник тока, лампочка, ключ и амперметр.
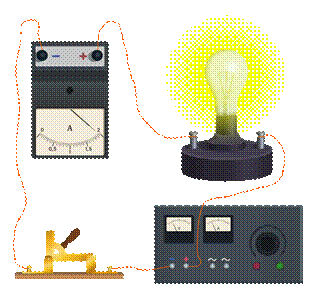
Если внимательно посмотреть на такую цепь, то не трудно заметить, что при таком соединении конец одного проводника соединяется с началом другого, его конец — с началом третьего и так далее.
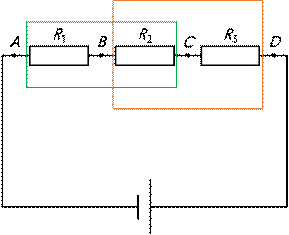
Таким образом, последовательное соединение — это такое соединение, при котором проводники (то есть потребители) имеют по одной общей точке. Так, в схеме, представленной на рисунке, для проводников R 1 и R 2, таковой является точка B, а для R 2 и R 3 — точка C.
Сравним токи в различных точках цепи. Для чего соберём цепь, состоящую из источника тока, ключа и двух лампочек. С помощью амперметра будем измерять силу тока в различных её участках: например, в точках А, В и С.
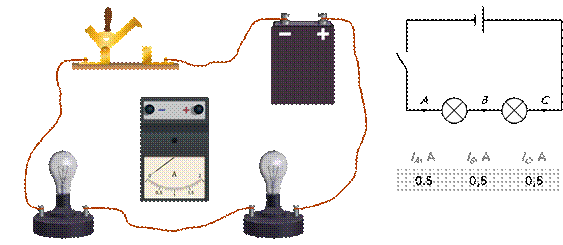
Опыт показывает, что при последовательном соединении сила тока во всех проводниках одинакова.
Действительно, при таком подключении один проводник следует за другим и, следовательно, все заряды, проходящие через первый из них, непременно проходят и через второй. Таким образом, в силу закона сохранения заряда, сила тока в каждом проводнике одинакова и равна полному току на рассматриваемом участке цепи: I 1 = I 2 = … = I.
|
|
Теперь сравним напряжение на каждом из проводников и общее напряжение цепи.
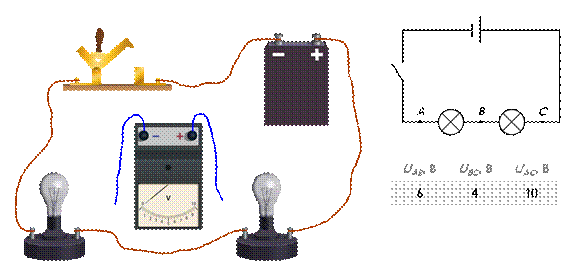
Опыт показывает, что при последовательном соединении полное напряжение в цепи, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: U = U 1 + U 2 + ….
Эта закономерность вытекает из физического смысла напряжения. Вспомните, что оно показывает, какую работу совершает электрическое поле при перемещении в нём электрического заряда. Как известно, эта работа совершается за счёт энергии электрического поля. А энергия, которая была израсходована на всём участке цепи, равна сумме энергий, расходуемых на отдельных проводниках, которые составляют этот участок.
Теперь, пользуясь результатами наших опытов, сравним сопротивления проводников с общим сопротивлением цепи.
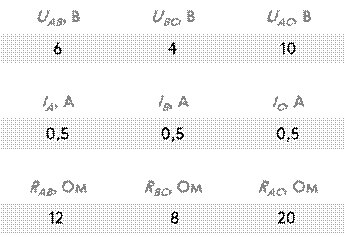
Таким образом, полное сопротивление группы последовательно соединённых проводников равно сумме сопротивлений отдельных проводников: R = R 1 + R 2 + ….
Рост сопротивления цепи при добавлении в неё новых проводников объясняется увеличением длины проводящей части:
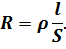
Поэтому сопротивление цепи становится больше сопротивления одного проводника.
На практике последовательное соединение нескольких проводников используется, например, в ёлочной гирлянде. Вы наверняка хорошо знаете, что если гирлянда вдруг гаснет, то это значит, что одна из лампочек либо перегорела, либо у неё отошёл контакт. Это ещё раз подтверждает уже известное вам утверждение, что ток при последовательном соединении проходит через все проводники и сила тока во всех частях одна и та же. Стоит нарушить где-то контакт — и ток прекращается во всей цепи.
|
|

Однако последовательное соединение электроприборов в быту не применяется. Предлагаем вам самостоятельно подумать почему.
Пример решения задачи.
Задача. Определите показания приборов в цепи, схема которой представлена на рисунке. Сопротивления резисторов R 1 = 40 Ом, R 2 = 60 Ом.
