Функция является обратимой, так как она монотонна.
6. Нулей функции нет, так как уравнение у = 0, то есть  корней не имеет.
корней не имеет.
7. Промежутки знакопостоянства: при  , так как
, так как
при 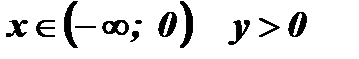
при 
при 
8. Функция ограничена снизу, так как  при
при  .
.
9. Любая показательная функция проходит через точку (0; 1), так как при
х = 0  .
.
Замечание:
1) При а > 1 функция возрастает тем быстрее, чем больше а;
2) При 0 < а < 1 функция убывает тем быстрее, чем меньше а.
| х |
| у |
| - 3 |
| - 2 |
| - 1 |

|

|
0 < а < 1 

| х | - 3 | - 2 | - 1 | ||||
| у | 
| 
| 
|
а > 1 а = 2 
| х | - 3 | - 2 | - 1 | ||||
| у | 
| 
| 
|
Упражнения:
1. Перечислите свойства функции и постройте ее график:
а)  ; б)
; б)  ; в)
; в) 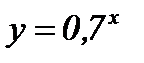 ; г)
; г)  .
.
2. Найдите множество значений функции:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
3. Сравните числа:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
4. Вычислите:
а)  ; б)
; б) 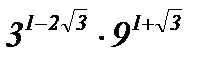 ; в)
; в) 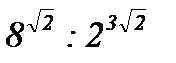 ; г)
; г)  .
.
5. Укажите, какая из данных функций является возрастающей, какая – убывающей на множестве действительных чисел R:
а)  ; б)
; б) 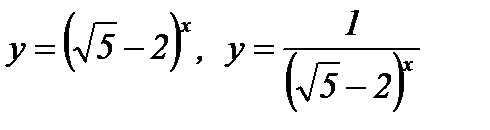 ;
;
в)  ; г)
; г)  .
.
2. Показательные уравнения.
Определение: Показательными уравнениями называются уравнения, содержащие переменную в показателе степени.
1) 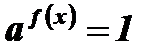 , а > 0, а ¹ 1
, а > 0, а ¹ 1
На основании определения степени с нулевым показателем решение уравнения 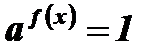 сводится к решению уравнения f(x)=0:
сводится к решению уравнения f(x)=0:
 .
.
Пример: Решить уравнение:  .
.
Решение:
 ; 1 = 20;
; 1 = 20;  ;
;
 ;
;  ;
;  ;
;
 ;
;  ; х1 = 2; х2 = 3.
; х1 = 2; х2 = 3.
Ответ: х1 = 2; х2 = 3.
Упражнения: Решить уравнение  :
:
1. а = 2 f (x)= x2- 40 x + 300;
2. а = 5 f (x)= (x2+ x - 2)(3- x);
3. а = 3  ;
;
4. а = 2 f (x)= x2- 7 x + 12;
5. a = 0,5  .
.
2) 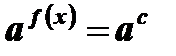 , а > 0, а ¹ 1
, а > 0, а ¹ 1
Левая и правая части уравнения  приведены к одному основанию. В этом случае корнями уравнения
приведены к одному основанию. В этом случае корнями уравнения  будут корни уравнения
будут корни уравнения  .
.
 .
.
Пример: Решить уравнения:
1)  .
.
Решение:  ;
;  ;
;  ;
;
 ;
; 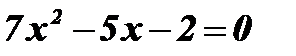 ;
;  ;
;  ;
;
 ;
;  ; х1 =
; х1 =  ; х2 = 1.
; х2 = 1.
Ответ: х1 =  ; х2 = 1.
; х2 = 1.
2)  .
.
Решение:  ; 128 = 27;
; 128 = 27;
 ;
;  ; 6 х = 7; х =
; 6 х = 7; х =  .
.
Ответ: х =  .
.
3)  .
.
Решение:
 ;
;  ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  ; х1 = - 1; х2 = 3.
; х1 = - 1; х2 = 3.
Ответ: х1 = - 1; х2 = 3.
Упражнения: Решить уравнения:
1.  ; ;
| 2.  ; ;
|
3.  ; ;
| 4.  ; ;
|
5.  ; ;
| 6.  ; ;
|
7.  ; ;
| 8. 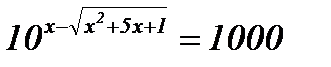 ; ;
|
9.  ; ;
| 10.  ; ;
|
11.  ; ;
| 12. 
|
3)  , а > 0, а ¹ 1, b > 0, b ¹ 1, а ¹ b
, а > 0, а ¹ 1, b > 0, b ¹ 1, а ¹ b
Уравнение решается делением обеих частей на  .
.
Пример: Решить уравнения:
1)  .
.
Решение: Разделим обе части уравнения на  .
.
 ;
;  ;
;  ; х - 2 = 0; х = 2.
; х - 2 = 0; х = 2.
Ответ: х = 2.
2)  .
.
Решение:  ;
;  ;
;  ;
;
Умножим обе части уравнения на  .
.
 ;
;  ;
;  ; х - 3 = 0; х = 3.
; х - 3 = 0; х = 3.
Ответ: х = 3.
Упражнения: Решить уравнения:
1)  ; ;
| 2)  ; ;
|
3)  ; ;
| 4) 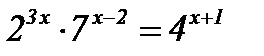 ; ;
|
5)  ; ;
| 6)  . .
|
4) 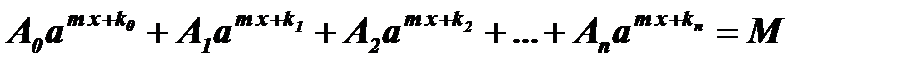 , а > 0, а ¹ 1
, а > 0, а ¹ 1
Особенностью уравнения является наличие одного и того же коэффициента перед х. Для решения этого уравнения выносят за скобки общий множитель  , где k i - наименьшее из чисел k0, k1 , k2, …, kп .
, где k i - наименьшее из чисел k0, k1 , k2, …, kп .
Пример:
1)  .
.
Решение: 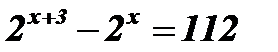 ;
;  ;
;  ;
;  ;
; 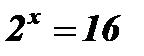 ;
;  ; х = 4.
; х = 4.
Ответ: х = 4.
2)  .
.
Решение:
 ;
;  ;
;
 ;
;  ;
;
 ;
;  ; 3х - 2 = 2х - 2; 3х - 2х = 2 - 2; х = 0.
; 3х - 2 = 2х - 2; 3х - 2х = 2 - 2; х = 0.
Ответ: х = 0.
3)  .
.
Решение:
 ;
; 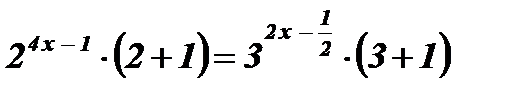 ;
;
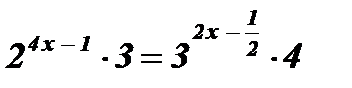 ;
; 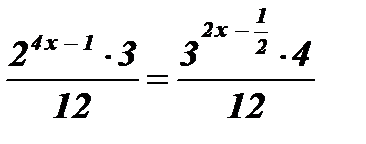 ;
;  ;
;
 ;
; 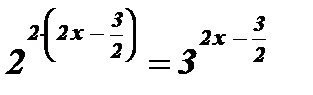 ;
;  ;
;
 ;
;  ;
;  ;
; 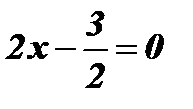 ;
;  .
.
Ответ:  .
.
Упражнения: Решить уравнения:
1)  ; ;
| 2)  ; ;
|
3) 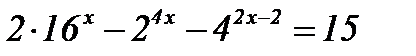 ; ;
| 4)  ; ;
|
5)  ; ;
| 6)  . .
|
5)  , а > 0, а ¹ 1
, а > 0, а ¹ 1
Уравнение  с помощью подстановки
с помощью подстановки 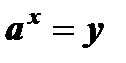 обращается в квадратное уравнение:
обращается в квадратное уравнение:  . Решив квадратное уравнение, найдем у1, у2. После этого решение уравнения
. Решив квадратное уравнение, найдем у1, у2. После этого решение уравнения  сводится к решениюдвух уравнений:
сводится к решениюдвух уравнений:  ,
,  .
.
Пример:
1)  .
.
Решение:  ;
;  ;
;  ;
;
 ;
;  ;
; 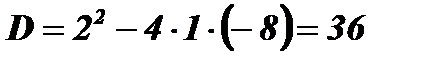 ;
;
 ;
; 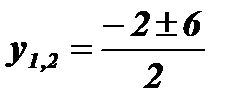 ; у1 = - 4; у2 = 2;
; у1 = - 4; у2 = 2;
 - уравнение корней не имеет, так как
- уравнение корней не имеет, так как  ;
;
 ; х = 1.
; х = 1.
Ответ: х = 1.
2)  .
.
Решение:
 ;
;  ;
;  ;
;
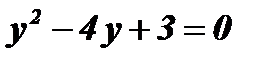 ;
;  ;
;  ;
;
 ;
;  ; у1 = 1; у2 = 3;
; у1 = 1; у2 = 3;
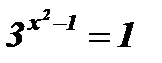 ; х2 - 1 = 0; х2 = 1; х1 = - 1; х2 = 1;
; х2 - 1 = 0; х2 = 1; х1 = - 1; х2 = 1;
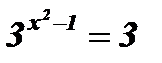 ; х2 - 1 = 1; х2 = 2; х3 =
; х2 - 1 = 1; х2 = 2; х3 =  ; х4 =
; х4 =  .
.
Ответ: х1 = - 1; х2 = 1; х3 =  ; х4 =
; х4 =  .
.
Упражнения: Решить уравнения:
1)  ; ;
| 2)  ; ;
|
3) 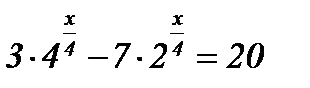 ; ;
| 4)  ; ;
|
5)  ; ;
| 6)  ; ;
|
7)  . .
|
6)  , а > 0, а ¹ 1, b > 0, b ¹ 1.
, а > 0, а ¹ 1, b > 0, b ¹ 1.
Отметим, что в выражении  показатели степеней в первом и третьем слагаемых вдвое больше показателей степеней во втором слагаемом. Такие выражения называются однородными 2-ого порядка. А уравнения вида
показатели степеней в первом и третьем слагаемых вдвое больше показателей степеней во втором слагаемом. Такие выражения называются однородными 2-ого порядка. А уравнения вида  называются однородными 2-ого порядка. Разделив уравнение на
называются однородными 2-ого порядка. Разделив уравнение на  , получим:
, получим:  .
.
Уравнение  с помощью подстановки
с помощью подстановки  обращается в квадратное уравнение:
обращается в квадратное уравнение:  . Решив квадратное уравнение, найдем у1, у2 и, возвращаясь к первоначальной переменной, получим два уравнения
. Решив квадратное уравнение, найдем у1, у2 и, возвращаясь к первоначальной переменной, получим два уравнения  и
и 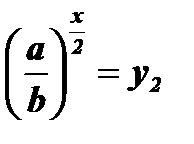 .
.
Пример:  .
.
Решение:  ;
;  ;
;
Разделим обе части уравнения на 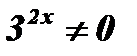 :
:
 ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  ; у1 =
; у1 =  ; у2 = 1;
; у2 = 1;
 ; х1 = 1;
; х1 = 1;  ; х2 = 0.
; х2 = 0.
Ответ: х1 = 1; х2 = 0.
Упражнения: Решить уравнения:
1)  ; ;
| 2) 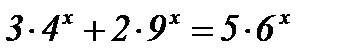 ; ;
|
3)  ; ;
| 4)  . .
|
Графический способ решения уравнений
Уравнение  можно рассматривать как задачу об отыскании таких значений переменной х, при которых значения двух данных функций равны.
можно рассматривать как задачу об отыскании таких значений переменной х, при которых значения двух данных функций равны.
Рассмотрим уравнение вида  . Графический способ решения такого вида уравнений заключается в отыскании приближенных значений абсцисс точек пересечения графиков функций
. Графический способ решения такого вида уравнений заключается в отыскании приближенных значений абсцисс точек пересечения графиков функций  и
и  в одной и той же системе координат.
в одной и той же системе координат.
| х2 |
| х1 |
| х |
| у |
| - 3 |
| - 2 |
| - 1 |

|

|
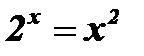 .
.
Решение:
у = х2
| х | - 3 | - 2 | - 1 | ||||
| у |

| х | - 3 | - 2 | - 1 | ||||
| у | 
| 
| 
|
Ответ: х1 » - 0,7; х2 = 2.
Упражнения: Решите графически уравнения:
1)  ; ;
| 2) 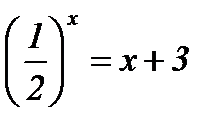 ; ;
|
3)  ; ;
| 4)  ; ;
|
5) 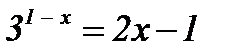 ; ;
| 6)  ; ;
|
7)  ; ;
| 8)  . .
|
3. Показательные неравенства.
Определение: Показательными неравенствами называются неравенства, содержащие переменную в показателе степени.
Решение простейших показательных неравенств основано на известном свойстве функции 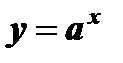 : показательная функция возрастает при
: показательная функция возрастает при  и убывает при
и убывает при 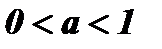 .
.


Пример: Решить неравенства:
1.  .
.
Решение:  .
.
Ответ: 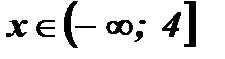 .
.
2.  .
.
Решение:  ;
;
а = 1> 0 ветви параболы направлены вверх;
х 2 + 3х = 0;  ;
;
| х |
| + |
| + |
| - |
| - 3 |
Ответ: 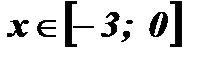
3.  .
.
Решение:
 ;
;  ;
;  ;
;  ;
;  ;
;
 ;
;  ;
;  .
.
Ответ: 
Упражнения: Решить неравенства:
1.  ; ;
| 2. 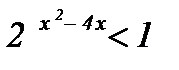 ; ;
|
3.  ; ;
| 4.  ; ;
|
5.  ; ;
| 6.  ; ;
|
7.  ; ;
| 8.  ; ;
|
9.  ; ;
| 10.  ; ;
|
13. 
|
4. Понятие логарифма. Основное логарифмическое тождество.
Необходимость возникновения нового понятия появилась из практической потребности при решении конкретных задач.
| х |
| у |
| - 3 |
| - 2 |
| - 1 |
а с= b
2 с = 2 Þ с = 1;
2 с = 3 Þ с = 1,…;
2 с = 4 Þ с = 2;
2 с = 7 Þ с = 2,…;
2 с = 8 Þ с = 3;
Определение: Логарифмомчисла b по основанию а называется показатель степени с, в которую надо возвести данное основание а, чтобы получитьчисло b.

Вывод:  .
.
 - основное логарифмическое тождество.
- основное логарифмическое тождество.
Замечание:
- Логарифмы чисел, вычисленные по одному и тому же основанию, образуют систему логарифмов.
- Систему логарифмов по основанию 10 называют системой десятичных логарифмов. Обозначение:
 .
. - Систему логарифмов по основанию е » 2,718281828459045 называют системой натуральных логарифмов. Обозначение:
 .
.
Пример:
1. Чему равен 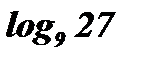 ?
?
Решение:  .
.
Ответ:  .
.
2. При каком основании  ?
?
Решение:  .
.
Ответ:  .
.
3. Найти число, логарифм которого при основании 64 равен  .
.
Решение:  .
.
Ответ:  .
.
Упражнения: Вычислить:  ;
;
1)  ; ;
| 2)  ; ;
| 3)  ; ;
|
4)  ; ;
| 5)  ; ;
| 6)  ; ;
|
7)  ; ;
| 8)  ; ;
| 9)  ; ;
|
10)  ; ;
| 11) 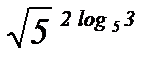 ; ;
| 12)  ; ;
|
13)  . .
|
5. Свойства логарифмов. Логарифмирование и потенцирование.
1)  , так как
, так как  .
.
2)  , так как
, так как  .
.
3) Логарифм произведения двух или нескольких положительных чисел равен сумме логарифмов сомножителей:
 .
.
4) Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя:  .
.
5) Логарифм степени положительного числа равен показателю степени, умноженному на логарифм основания:  .
.
6) Логарифм корня из положительного числа равен логарифму подкоренного выражения, деленному на показатель корня:
 .
.
Пример: Вычислить:
-
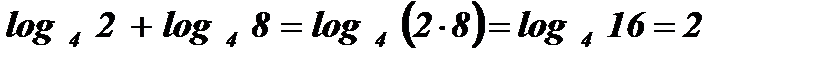 ;
; -
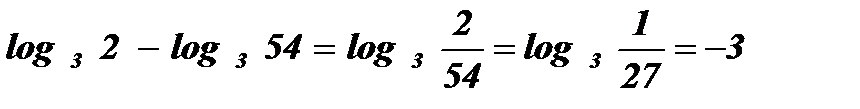 ;
; -
 ;
; -

 ;
;
-
 ;
; -
 .
.
Определение: Логарифмированием данного выражения называется представление логарифма этого выражения через логарифмы входящих в него элементов.
Замечание: Сумма и разность выражений не логарифмируются.
Пример:
1. Прологарифмировать данное выражение:
1)  .
.
Решение:  .
.
2) 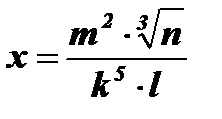 .
.
Решение: 
3)  .
.
Решение:
 .
.
 .
.
2. Вычислить:  .
.
Решение:  .
.
Ответ:  .
.
Определение: Потенцированием называется нахождение выражения по его логарифму. Потенцирование – это действие,обратное логарифмированию.
Пример: Пропотенцировать:  .
.
Решение:
 ;
;
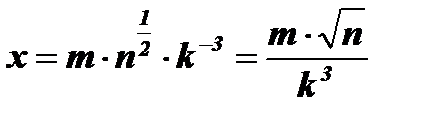 .
.
Ответ:  .
.
Упражнения:
1. Вычислить:
1)  ; ;
| 2)  ; ;
|
3)  ; ;
| 4)  ; ;
|
5)  ; ;
| 6)  ; ;
|
7)  ; ;
| 8) 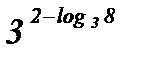
|
- Прологарифмировать данное выражение:
1)  ; ;
| 2)  ; ;
|
3) 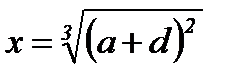 ; ;
| 4)  ; ;
|
5)  ; ;
| 6) 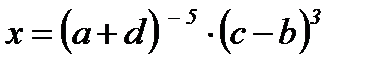 ; ;
|
7) 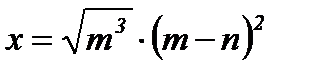 ; ;
| 8)  ; ;
|
9)  . .
|
- Пропотенцировать:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  .
.
- Найти х, если:
1)  ;
;
2)  ;
;
3)  .
.
6. Логарифмическая функция, ее свойства и графики.
Определение: Функция, обратная показательной функции, называется логарифмической.
 - показательная функция;
- показательная функция;
 Û
Û  ;
;
 - логарифмическая функция.
- логарифмическая функция.
- Область определения функции:
 , так как по определению
, так как по определению 
- Множество значений функции:
 , так как показатель степени может быть любым действительным числом.
, так как показатель степени может быть любым действительным числом.
Вывод: График логарифмической функции расположен в первой и четвертой координатных четвертях.
- Функция не является ни четной ни нечетной, так как её область определения не симметрична относительно начала координат.
- Функция является монотонной:
1) при 0 < а < 1 
 – убывающая функция;
– убывающая функция;
2) при а > 1 а = 2  – возрастающая функция.
– возрастающая функция.
- Функция является обратимой, так как она монотонна:
 - логарифмическая функция;
- логарифмическая функция;

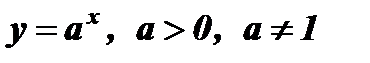 - показательная функция.
- показательная функция.
- у = 0;
 ; х = 1 - нуль функции.
; х = 1 - нуль функции. - Промежутки знакопостоянства:
1) при 0 < а < 1
 ;
;
 .
.
2) при а > 1
 ;
;
 .
.
- Функция является неограниченной сверху и снизу.
- Любая логарифмическая функция проходит через точку (1; 0), так как при х = 1
 .
.
Замечание: Для построения графика логарифмической функции можно воспользоваться свойством графиков взаимно обратных функций: графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов, то есть относительно прямой у = х.
 (0 < а < 1)
(0 < а < 1)
| х | 
| 
| 
| ||||
| у | - 3 | - 2 | - 1 |
| х |
| у |
| - 3 |
| - 2 |
| - 1 |
| - 1 |
| - 2 |
| - 3 |

|

|
| у = х |
 (а > 1)
(а > 1)
| х | 
| 
| 
| ||||
| у | - 3 | - 2 | - 1 |
| х |
| у |
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2019-01-11 Нарушение авторских прав и Нарушение персональных данных