Лабораторная работа №1
ИЗУЧЕНИЕ ТЕОРИИ КОЛЕБАНИЙ ПРУЖИННЫХ МАЯТНИКОВ
ЦЕЛЬ РАБОТЫ
Задачей данной работы является ознакомление с простейшим случаем гармонических колебаний пружинного маятника, которые в воздухе можно считать незатухаю-щими. Работа складывается из двух разделов. Первый раз-дел работы (упражнение 1-2) – изучение собственных гармонических колебаний с одной степенью свободы (рис.1.1, а). Второй раздел работы (упражнения 3-4) – изу-чение системы двух связанных маятников (рис. 1.1, б, 1.1, в).
 |
Приборы и принадлежности
- набор пружин и грузов
- измерительная установка для отсчета отклонений грузов
- секундомер
МЕТОДИКА ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА
Пружинный маятник – это грузик, подвешенный на пру-жине. После отклонения от положения равновесия он будет совершать вертикальные гармонические колебания, если упругая пружина такова, что сила деформации пропорци-ональна величине удлинения пружины (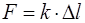 , где
, где  – коэффициент упругости).
– коэффициент упругости).
Под действием силы тяжести грузика она растянется на длину  (рис. 1.2) – это будет соответствовать условию, что сумма сил, действующих на массу
(рис. 1.2) – это будет соответствовать условию, что сумма сил, действующих на массу  , равна нулю (
, равна нулю ( ),или условию минимума потенциальной энергии системы:
),или условию минимума потенциальной энергии системы:
 или
или 
 .
.
 |
При отклонении от положения равновесия на величину x появляется возвращающая сила  (рис. 1.2); тело на-чинает колебаться.
(рис. 1.2); тело на-чинает колебаться.
Уравнение движения тела:
 ;
;
 , т.е.
, т.е. 

– уравнение собственных незатухающих колебаний с частотой
 .
.
Решением уравнения будет (при условии начального максимального отклонения)
 .
.
Период колебаний равен
 , т.е.
, т.е.  . (1.1)
. (1.1)
Из (1.1) видно, что с увеличением коэффициентов упру-гости ( ) пружины растет частота колебаний и уменьшается период колебаний.
) пружины растет частота колебаний и уменьшается период колебаний.
Характер собственных колебаний пружинного маятника не зависит от силы тяжести, а зависит только от перемен-ной возвращающей силы.
Система двух пружин с разными коэффициентами упру-гости, связанных друг с другомпо схеме рис.1.1, б или 1.1, в представляет собой связанную систему с двумя степенями свободы. При колебаниях системы (рис.1.1, б) смещения у разных пружин в один и тот же момент времени не будут одинаковыми:  . Во время колебаний будут изме-няться одновременно две величины
. Во время колебаний будут изме-няться одновременно две величины  и
и 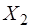 , т.е. если мы резким толчком выведем из положения равновесия только нижнюю пружину, то возникшие колебания обязательно пе-редадутся к верхней пружине. Поэтому при анализе коле-баний мы обязаны учитывать одновременное движение обе-их пружин. Подобная система имеет две степени свободы.
, т.е. если мы резким толчком выведем из положения равновесия только нижнюю пружину, то возникшие колебания обязательно пе-редадутся к верхней пружине. Поэтому при анализе коле-баний мы обязаны учитывать одновременное движение обе-их пружин. Подобная система имеет две степени свободы.
Наблюдая колебания за некоторое сравнительно неболь-шое время, когда еще не сказалось действие сил трения, мы увидим, что колебания каждого из маятников негармонич-ны. Это объясняется перекачкой энергии от одной пружины к другой. Колебания будут носить характер биений. Время  , за которое пружины обменялись энергией, называется периодом биений. Механическая энергия будет полностью переходить из одной пружины в другую, пока она не прев-ратится в тепловую и колебания не прекратятся.
, за которое пружины обменялись энергией, называется периодом биений. Механическая энергия будет полностью переходить из одной пружины в другую, пока она не прев-ратится в тепловую и колебания не прекратятся.
Характер биений в случае двух пружин во многом зави-сит от масс пружин и их упругости (упругих свойств). Чем меньше массы пружин, тем более гармоничными становятся колебания. Если пренебречь массами пружин, то систему пружинных маятников, изображенных на рис.1.1, б, в можно представить как пружинный маятник с одной степенью сво-боды, обладающий некоторым эффективным коэффициен-том упругости.
Формула эффективного коэффициента упругости для схемы последовательного соединения пружин выводится из предположения, что в точке соединения пружин силы упру-гости обеих пружин одинаковы. Тогда, если мы обозначим через  удлинение пружины с коэффициентом упругости
удлинение пружины с коэффициентом упругости  , а через
, а через 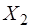 удлинение пружины с коэффициентом упру-гости
удлинение пружины с коэффициентом упру-гости  , то можно записать
, то можно записать
 . (1.2)
. (1.2)
Общее удлинение обеих пружин
 . (1.3)
. (1.3)
Тогда
 . (1.4)
. (1.4)
Подставляя вместо 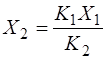 , получим выражение для эффективного коэффициента упругости:
, получим выражение для эффективного коэффициента упругости:
 ,
,
откуда
 . (1.5)
. (1.5)
Период колебаний такого маятника равен  , или
, или
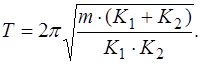 (1.6)
(1.6)
Формула эффективного коэффициента упругости маят-ника, составленного из двух параллельно соединенных пру-жин, получается из предположения, что если груз подвешен к точке, относительно которой моменты сил упругости и весов частей планки, разделенной точкой подвеса равны, то вращения нет. Cледовательно,
 ,
,  . (1.7)
. (1.7)