LEARNING OPERATIONAL SPACE CONTROL
Jan Peters, Stefan Schaal
Departments of Computer Science & Neuroscience
University of Southern California Los Angeles, CA 90802
Email: { jrpeters, sschaal }@usc.edu
The International Journal of Robotics Research, 2008
ОБУЧЕНИЕ УПРАВЛЕНИЮ В ОПЕРАЦИОННОМ ПРОСТРАНВЕ
Аннотация — С одной стороны, управление в оперативном пространстве имеет важное значение для робототехники, а также легко интерпретируется аналитически, с другой стороны, чрезвычайно сложно добиться точного управления при ошибках моделирования, которые неизбежны в сложных роботах (например, роботах-гуманоидах). В таких случаях методы обучения управлению предлагают интересную альтернативу аналитическим алгоритмам. Однако возникающая в результате задача обучения плохо определена, так как она требует изучения обратного отображения (обычно) избыточной системы, которая (как известно) страдает от свойства невыпуклости пространства решений, т.е. система обучения может генерировать команды, которые пытаются направить робота в физически невозможные конфигурации. Первая важная догадка этой статьи: физически правильное решение обратной задачи существует в том случае, если изучение обратного отображения выполняется подходящим кусочно-линейным способом. Второй важный компонент статьи: многие методы управления в операционном пространстве определяются в терминах задачи оптимального управления с ограничениями. Функция стоимости, связанная с этой задачей оптимального управления, позволяет сформулировать алгоритм обучения, который автоматически синтезирует согласованное на глобальном уровне разрешение избыточности при обучении управлению в операционном пространстве. С точки зрения машинного обучения, проблема соответствует задаче обучения с подкреплением, которая максимизирует немедленное вознаграждение и использует алгоритм поиска политики максимизации ожидания. Оценки робота-манипулятора с тремя степенями свободы иллюстрируют осуществимость предложенного подхода.
I. ВВЕДЕНИЕ
Управление в оперативном пространстве является одним из наиболее элегантных подходов к задаче управления благодаря возможности динамического согласования управления, совместимого по силе управления, иерархического управления и мн.др. благоприятных свойств, с приложениями от управления захватом манипулятора [1], [2] до балансировки и выполнения ходьбы человекоподобными роботами [3]. Если модель робота точно известна и управление в операционном пространстве хорошо понятно, это дает множество различных альтернативных решений, включая управление скоростью разрешенного движения, управление разрешенным ускорением и управление на основе силы [4]. Тем не менее, особенно, если требуется совместимое (compliant) (т.н. режим с малым усилием (low-gain)) управление в оперативном пространстве (как во многих новых роботизированных системах, которые должны безопасно работать вместе с человеком), это управление становится в большой степени трудным из-за присутствия немоделируемых нелинейных параметров, что, в свою очередь, приводит к снижению точности и даже к непредсказуемому и нестабильному поведению системы робота. Как потенциальное решение этой проблемы, методы обучения управлению кажутся многообещающими. Но для методов обучения нелегко обеспечить высокоструктурированные знания, требуемые в традиционных законах управления в оперативном пространстве, в т.н. Якобианах, матрицах инерции и кориолисовых/центростремительных и гравитационных силах. Поскольку все эти члены уравнений не наблюдаемы и, следовательно, не подходят для формулирования метода обучения с учителем, которые традиционно используются в подходах обучения управлению [5].
В этой статье предлагаем новый подход обучения управлению в оперативном пространстве, который избегает извлечения таких структурированных знаний и скорее направлен на непосредственное изучение алгоритма управления в оперативном пространстве. Для разработки нашего подхода будем действовать так:
1. рассмотрим управление в оперативном пространстве, обсудим, где обучение может быть полезно.
2. рассмотрим управление в оперативном пространстве как задачу обучения и обсудим, почему стандартные методы обучения не могут применяться напрямую.
Используя альтернативное понимание управления в оперативном пространстве как задачу оптимального управления, переформулируем её как явную задачу обучения с подкреплением или задачу поиска политики. Предложим новые алгоритмы для изучения некоторых из наиболее стандартных типов законов управления в оперативном пространстве. Эти новые методы будут оценены на моделируемой руке робота с тремя степенями свободы.
A. Обозначения и замечания.
В статье предполагаем стандартную модель твёрдого тела для описания робота:
M(q) q¨ + C(q, q˙) + G(q) + ε(q, q˙) = u, (1)
где q, q˙, q¨ ∈ Rn – координаты, скорости и ускорения сочленений робота, соответственно. Крутящие моменты, генерируемые двигателями робота, описываются командами движений u ∈ Rn. M(q) – тензор инерции или матрица масс, C(q, q˙) – силы Кориолиса и центростремительные силы, G(q) – гравитация и ε(q, q˙) – вне-модельные нелинейные параметры.
Управление в операционном пространстве (operational space) есть намерение выполнить траектории или силы [1], заданные в координатной системе актуальных целей. Хорошо известный примером является робот-манипулятор, где управление осуществляется позицией и ориентацией захвата [1], [2]; множество будущих приложений связаны с управлением центром тяжести при балансировании роботом с ногами, который перемещается в операционном пространстве [3]. Позиция и ориентация x∈Rm контролируемого элемента (захвата) в пространстве целей (task space) заданы прямой кинематикой x = fKinematics(q), а скорость и ускорение в пространстве целей, есть её производные:
x˙ = J(q) q˙; x¨ = J(q) q¨ + J(q)˙ q˙, (2)
где Якобиан J(q) = dfKinematics(q)/dq. Предположим, что робот в общем c избыточностью (redundant), т.е. имеет больше степеней свободы, чем требуется для задачи, или, что эквивалентно, n > m.
B. Управление в операционном пространстве как задача оптимального управления
Используя в качестве примера структуру отслеживания траектории, общую задачу управления в оперативном пространстве можно описать следующим образом: создать закон управления
u = fcontrol (q,q˙,xd,xd˙, xd¨)
который контролирует робота вдоль всей траектории q(t),q(t)˙,q¨(t) в пространстве сочленений (joint space) также, как следование контролируемого элемента (захвата) по требуемой траектории в пространстве целей xd(t),xd˙(t),xd¨(t). Это задача основательно обсуждалась с поздние 1980е гг. [1], [2] и, получила разрешение в виде всем хорошо известных законов управления [4]. Важная новая мысль недавно обнаружена [6] состоит в том, что многие предложенные в литературе контроллеры могут быть выведены, как решение граничной оптимизационной задачи:
, (3)
где N – положительно определённая метрика, которая взвешивает вклад в функцию стоимости команд движения. Эталонный аттрактор в пространстве целей
xref¨ = xd¨(t) + Kd(xd˙(t) − x˙(t)) + Kp(xd(t) − x(t))
с матрицами усиления (gain matrices) Kd и Kp. Итоговые законы управления или решение оптимизационной задачи имеет общую форму [6]:
u = N−1/2(JM−1N−1/2) + (xref¨ − J˙q˙+ JM−1F), (4)
c F(q,q˙)=C(q,q˙)+G(q)+ε(q,q˙). Запись D+ определяет псевдо-обратную матрицу, как D+D=I, DD+=I. Корень матрицы (matrix root) D1/2 определяется, как D1/2D1/2 = D.
Например, контроллер разрешённого ускорения Hsu и ко. [2] (без оптимизации ноль-пространства) есть результат использования метрики N=M−2, для которой следует u = MJT (xref¨ − J˙q˙)+F, что соответствует каскаду законов управления обратной динамики и обратной кинематики. Другим примером является формулировка Хатиба управления в оперативном пространстве [1], определяемая метрикой N=M−1, определяется, как:
u = JT (JM−1 JT)−1 (xref¨ - J˙q˙+ JM−1 F). (5)
Решение Хатиба является особенным, т.к. N=M−1 является единственной метрикой, при которой генерируемые крутящие моменты соответствуют согласованным физическим крутящим моментам, тянущим робота по траектории [6], [7]. Т.е. метрика используется природой согласно принципу Гаусса [7], [8] и является инвариантной при переходе между системами координат сочленений [9]. Другие метрики, такие как N=const, могут использоваться для отличного распределения требуемых сил, например, так, чтобы более сильные двигатели получали большую часть генерируемых сил [6].
Даже при достижении траектории идеальной с точки зрения следования цели, это может приводить к неблагоприятным положениям или даже к нестабильностям в пространстве сочленений (см. Пример 1). Для обработки таких случаев необходимо включить дополнительные элементы управления, которые не влияют на производительность следования цели, но обеспечивают благоприятное поведение в пространстве сочленений. С точки зрения структуры оптимизации, следует выбрать номинальный закон управления u0 (например, силу, которая тянет робота в положение покоя u0=−KDq˙− KD(q - qrest)), и затем решить краевую задачу оптимизации:
, (6)
где u1=u−u0 – компонента управления в пространстве целей. Общее решение задано:
, (7)
,
где второе слагаемое осуществляет номинальный закон управления u0 в ноль-пространстве первого слагаемого. В случае, если имеется больше, чем две цели, они могут быть вложены похожим образом, приводя задачу к общей структуре иерархического управления [3], [6].
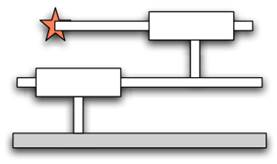(a) Робот с 2 призматическими степенями свободы
| 
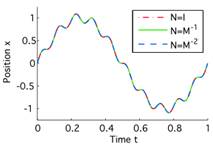(b) Позиция захвата x (все траектории совмещаются идеально с эталонной траекторией)
|
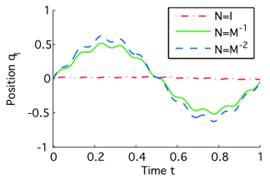(c) Позиция сочленения q1
| 
(d) Позиция сочленения q2
|
| Рис. 1.Применительно к призматическому роботу из Примера 1, показанного в (а), три закона управления для метрик N = I (пунктирная красная линия), N = M-1 (сплошная зеленая), N = M-2 (пунктирная синяя) приводят в (b) к одинаковому отслеживанию в пространстве целей, но в (c,d) к очень различному поведению в пространстве сочленений. См. Пример 1 для получения доп. информации. |
Пример 1: Иллюстрация следования в операционном пространстве захвата с позицией x = q1+q2 призматического робота с двумя параллельными связями с позициями сочленений q1,q2, см. рис. 1. Матрица масс M = diag (m1,0)+m2= 1 с массами m1=m2=1 ( 1 обозначает матрицу, у которой все коэффициенты = 1). Внутренние силы – F=0, Якобиан – J = [1,1]T и его производная J˙=0. Если не выбрано управление в пространстве сочленений то, u0=0, тогда закон управления в форме уравнения (4) для выполнения задачи будет xref¨=xd¨+Kd(xd˙−x˙)+Kp(xd−x). В результате будет нестабильное поведение для большинства метрик N. При добавлении u0=−KDq˙−KDq, тянущего робота по направлению qrest=0, получаем стабильное следование с очень разными свойствами, которые можно наблюдать на рис.1: (i) метрика N=I приводит к результату, когда второе звено ведёт захват, а компонента ноль-пространства стабилизирует первое звено, (ii) метрика N = M-1 распределяет задачу на оба звена равномерно и заставляет компоненту ноль-пространства развязывать эти два звена, в то время, как (iii) метрика N = M-2 просто минимизирует квадрат ускорения.
Используем этот простой пример робота (Пример 1) для наглядной демонстрации разных иных проблем ниже, он даёт для них простое аналитическое понимание и графическую визуализацию.
C. Зачем следует обучаться управлению в операционном пространстве?
В случае, когда имеется аналитическая модель робота и её параметры оценены достаточно точно, управление в операционном пространстве будет успешным [1], [3], [4]. Однако, во многих новых сложных роботизированных системах (например, гуманоидных роботах, космических роботах и т.д.) аналитические модели динамики робота непригодны из-за значительных отклонений от идеализированных теоретических моделей (таким, как динамика твердого тела). Например, в нашем опыте с антропоморфными роботами вне-модельные нелинейные эффекты были вызваны сложной динамикой гидропривода, гидравлическими шлангами и кабельными жгутами, проложенными вдоль легкой конструкции робота, а также сложными эффектами трения. Попытки смоделировать такие нелинейные параметры малопригодны из-за утраты общности и сложности получения полезных моделей для неизвестных эффектов.
Пример 2: в призматическом роботе из Примера 1 совсем небольшие вне-модельные нелинейные параметры создают сильный эффект. Если предполагаемая матрица масс робота: M˜= diag (m1,0)+m2=1 отличается только от M на M12-M12˜=M21-M21˜= 0.5 sin (q1+q2), т.е. из-за вне-модельных свойств кабелей полученный закон управления приводит к нестабильному и непредсказуемому поведению в нуль-пространстве, несмотря на то, что теоретически точное отслеживание в пространстве целей всё ещё возможно. В реальной физической системе чрезвычайное поведение в нулевом пространстве насыщает двигатели робота так, что даже отслеживание в пространстве целей ухудшается, и вся система управления становится нестабильной.
Пример 2 демонстрирует, как небольшая ошибка моделирования снижает производительность закона управления в оперативном пространстве и может привести к нестабильности в пространстве сочленений даже для простых роботов. Для легких роботизированных рук или роботов-гуманоидов такие проблемы становятся ещё более частыми, с ними трудно справиться. Традиционно эту проблему решает инженер, улучшающий аппроксимацию установки вручную; однако управления в оперативном пространстве лёгких роботов в режиме малого усилия трудно моделировать, обучение является новой многообещающей альтернативой, оно будет обсуждаться в разделе II.
II. LEARNING METHODS FOR OPERATIONAL SPACE CONTROL
Изучение управлению в оперативном пространстве манипуляторов с избыточностью является в значительной степени неисследованной проблемой, и в литературе есть только несколько связанных примеров. Среди них, подходы обучения управлению на уровне задач фокусировались главным образом на управлении конечным эффектором обратной кинематики [10] - [14], то есть изучали отображение обратной кинематики, чтобы создать соответствующие опорные траектории в пространстве сочленений, которые должны исполняться в соответствии с данным управляющим законом в пространстве сочленений. Сочетание изученной обратной кинематики и изученного регулятора обратной динамики [10], [13], [14] можно найти только в литературе. Насколько нам известно, в настоящее время общепринятые подходы к обучению не учитывают законы о полном управлении в оперативном пространстве с избыточностью.
А. Можно ли научиться управлению в оперативном пространстве?
Обучение управлению в оперативном пространстве эквивалентно получению отображения (q, q˙, xref ¨) → u из выборочных данных с использованием аппроксимации функции. Однако, поскольку размерность эталонной траектории пространства целей xref ¨ ниже, чем у команды движения u, существует бесконечно много решений для u для большинства положений суставов q и скоростей суставов q˙. Для иллюстрации в Примере 2 возьмём линейный случай без компоненты нулевого пространства, это отображение соответствует линии на плоскости возможных законов управления, это показано двумя линиями на рисунке 2 (а).
Команды движения u1 Команды движения u2
Рис. 2. На рисунке (а) показано, как разные наборы данных приводят к разным решениям, когда каждая точка данных обрабатывается с одинаковой важностью (синяя пунктир-точечная линия соответствует синим ромбам, а красная пунктирная линия - красным кружкам). Если же (b) эти точки данных взвешены с использованием Гауссовой функции затрат (здесь обозначенной метрикой N=M−1 в виде сплошных тонких черных линий), решения для различных наборов данных будут согласовано приближаться к оптимальным решениям (сплошная голубая линия). В то время, как для линейного призматического робота подходит любое решение из (а), для нелинейных роботов разные локальные решения должны создавать согласованное глобальное решение. Горизонтальные бледно точечные линии в (a) и (b) указывают очертания равного ускорения в пространстве целей.
Основная проблема, описанная впервые в контексте обучения инверсной кинематики [11], [14], возникает в случае робота с поворотными суставами: команды движения u для достижения одинакового эталонного ускорения xref ¨ больше не образуют выпуклое множество. Таким образом, при изучении обратного отображения (q, q˙, xref ¨) → u алгоритм обучения будет усредняться по несвязанным наборам решений, что может привести к неверным решениям задачи обучения. Поэтому проблема обучения плохо обусловлена, так что непосредственное обучение с учителем по образцам не подходит.
Тем не менее, проблемы выпуклости могут быть решены путем использования пространственно локализованной системы обучения с учителем, в нашем случае, она локализована как на основе положения в пространстве, так и скорости движения в суставе – такой подход был впервые введён в контексте обучения обратной кинематике [12], [14]. Осуществимость этой идеи может быть продемонстрирована простым усреднением по комбинации уравнений (2) и (1), что приводит к усреднению по пространственной позиции q и скорости q˙ точно так же, имеем
, (8)
, т.е. в окрестности одного и того же q, q˙, конкретное 
всегда будет соответствовать точно одному конкретному 
[2]. Следовательно, локально линейные контроллеры
, (9)
могут использоваться, если они активны только в области вокруг q,q˙ (обратите внимание, был добавлен постоянный вход в уравнение (9) для учёта пересечения линейной функции). С точки зрения техники управления, этот аргумент соответствует пониманию того, что когда мы можем линеаризовать установку в определенном регионе, мы можем найти локальный закон управления в этом регионе, рассматривающий (treating) установку как линейную и, как правило, у линейной системы не возникает проблем с невыпуклостью пространства решений при обучении обратной функции.
Далее необходимо рассмотреть, как найти подходящую кусочную линеаризацию для локально линейных контроллеров. Для этой цели обучим локально линейную модель прямого или прогнозирующего действия
,(10)
Обучение этой прямой модели стандартная задача обучения с учителем, т.к. отображение гарантировано будет подходящей (proper) функцией. Методом обучения такой прямой модели, которая автоматически также изучает локальную линеаризацию, является Локально-Взвешенная Проекция Регрессии (Locally Weighted Projection Regression - LWPR) [15], быстрый метод онлайн-обучения, который масштабируется на множество измерений, был использован для управления обратной динамикой роботов-гуманоидов, и может автоматически определять количество локальных моделей, которые необходимы для представления функции. Принадлежность к локальной модели определяется весом, сгенерированным из ядра Гаусса:
, (11)
с центром в ci в (q,q˙) -пространстве и ограниченный shaped по метрике расстояния Di. Более подробное описание этого статистического алгоритма обучения см. в [15].
Для каждой локальной прямой модели, созданной LWPR, автоматически создаем локальный контроллер. Этот подход парного объединения предикторов и контроллеров связан с архитектурой MOSAIC [16], где качество прогнозирования цели используется для выбора локального контроллера, который должен быть использован для задачи.
Б. Объединение локальных контроллеров и обеспечение согласованного устранения избыточности
Для того, чтобы управлять роботом с помощью этих локальных законов управления, их необходимо объединить в согласованный глобальный закон управления. Комбинация задается взвешенным средним [15]:
, (12)
где каждый закон управления ciβ(q,q˙,xref¨) действителен только в своей локальной области, вычисленной по wi(q,q˙), а βi являются параметрами каждого локального закона управления в операционном пространстве.
Однако, хотя отображения (q, q˙, xref ¨) → u можно правильно изучать локально в окрестности некоторого q,q˙, из-за избыточности в роботизированной системе, нет никакой гарантии, что все локальные отображения находят решение одного типа. Эта проблема обусловлена зависимостью обратного решения от распределения обучающих данных в каждой локальной модели, то есть разные распределения будут выбирать разные решения для обратного отображения из бесконечности возможных инверсий. На рисунке 2(а) демонстрируем этот эффект. Хотя эта проблема не является разрушительной для призматического робота из примера 1, она приводит к серьезным проблемам для любого нелинейного робота, требующего нескольких согласованных линейных моделей. Существуют два разных подхода к решению таких проблем:
(1) путём смещения (bias) системы, с использованием пред-обработанного набора данных, в направлении, в котором она могла произвести одно конкретное обратное решение [14],
или
(2) путём добавления функции затрат/вознаграждений, которая отдаст предпочтение определенному виду решения
(пример на рис. 2 (б), будет обсуждаться позже).
При первом подходе не хватает общности, это может привести к смещению (bias) обучаемой системы, т.ч. задача не будет больше выполняться должным образом. Основным недостатком второго подхода является то, что выбор функции затрат/вознаграждений в целом нетривиален и определяет алгоритм обучения также, как выученное решение.
Важнейший компонент нахождения принципиального подхода к этой проблеме несоответствия основан на обсуждении в разделе I-B и предыдущей работе [6]. Управление в оперативном пространстве можно рассматривать как краевую оптимизационную задачу с функцией стоимости – уравнением (3). Таким образом, основанный на функции стоимости подход для создания согласованного набора локальных контроллеров для управления в оперативном пространстве может быть основан на понимании этого. Функцию стоимости можно превратить в немедленное вознаграждение r(u), выполнив ее через экспоненциальную функцию:
,
где σ - коэффициент масштабирования, а команда в пространстве целей u1=u-u0 может быть вычислена с использованием требуемого поведения в нуль-пространстве u0 (например, тяга к положению покоя, как описано в разделе I-B). Коэффициент масштабирования σ не влияет на оптимальность решения u, поскольку он действует как монотонное преобразование в этой функции стоимости. Тем не менее, он может значительно повысить эффективность алгоритма обучения, когда для обучения доступны только разреженные данные (т.е. для большинства интересующих роботов, т.к. многомерные пространства действий сложных роботов вряд ли когда-либо будут заполнены данными)[3]. Эти локальные награды позволяют нам переформулировать нашу задачу обучения как задачу обучения с подкреплением с немедленным вознаграждением [18], она будет обсуждаться в разделе II-C.
Теперь можно сформулировать алгоритм обучения с учителем для локальных контроллеров в операционном пространстве. Все данные, взятые у реального робота, автоматически удовлетворяют уравнению ограничений задачи (3)(task constraint) иуравнению динамики твердого тела (1), аналогично задаче самообучения. Таким образом, для обучения локальных контроллеров в операционном пространстве получена локальная задача линейной регрессии, которая обучается главным образом на наблюдаемых командах движения uk, которые имеют высокие вознаграждения r(uk) в каждой активной локальной модели ciβ(q,q˙,xref¨). Интуитивное решение состоит в использовании регрессии с весами-наградами для нахождения решения, которое минимизирует:
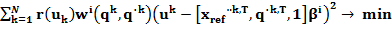, (13)
для каждого контроллера i. Решение этой задачи хорошо известная формула взвешенной регрессии:
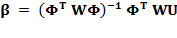, (14)
со строками в матрицах Φ и U:
Φk = [xref¨k,T,q˙k,T,1],
Uk = uk,T,
Wi = r(ui) w(qi,q˙i).
При использовании решения регрессии с весами-наградами, оно сходится к глобально согласованному решению для всех локальных контроллеров. Алгоритм обучения показан в Таблице I вместе с дополнительным компонентом, полученным в разделе II-C. Обратите внимание, что этот шаг был возможен только благодаря определяющей функции стоимости в уравнении (6) из нашей предыдущей работы.
C. Перефразированная, как задача обучения с подкреплением
Изначально этот алгоритм выведен с точки зрения взвешенной регрессии. Однако эта точка зрения не является полностью удовлетворительной, поскольку она всё ещё имеет открытый параметр σ2, который определяет скорость сходимости обучающихся контроллеров. Альтернатива в рамках обучения с подкреплением, позволяет вывести предыдущий алгоритм вместе с правилом вычисления σ2, используя подход, аналогичный предложенному Dayan & Hinton [18]. Для этой цели предположим, что у уже есть процесс выборки данных (sampling process) или политика выборки π˜(u), например, робот движется по полиномиальным траекториям 5-го порядка в пространстве сочленений в направлении случайно выбранных объектов в пространстве сочленений, используя простой PD-контроллер в пространстве сочленений. Кроме того, уже имеются локальные политики стохастического управления, заданные, например:
где N – нормальное распределение. Для простоты в этой статье предположим, что дисперсия Σ нормального распределения фиксирована, но она может быть включена в алгоритм ниже также, как βi. При такой настройке, хочется подогнать параметры локальных контроллеров таким образом, чтобы минимизировать ожидаемый возврат:
, (15)
немедленного вознаграждения (следовательно, переменная состояния q,q˙,xref¨ убирается из уравнения, присутствует неявно). Эта максимизация не возможна напрямую, однако можно максимизировать нижнюю границу преобразования log J(θ):
где ε – члены, независящие от параметров локальных контроллеров βi или открытого параметра σi2; устанавливаем q(uk) = π ˜ (u) r(u) wi(q,q˙), как в [18], как фиксированная выборка данных. Это дает два шага алгоритма максимизации ожидания, т.е. вычисление Q(βi,σi2) и максимизация нижней границы путём максимизации Q(βi, σi2). Шаг максимизации [βi, σi2]T = argmaxβ,ˆσ2 Q(ˆβ, ˆσ2) можно получить, задав ∂Q(ˆβ,ˆσ2)/∂ˆβ = 0 и ∂Q(ˆβ,ˆσ2)/∂(ˆσ2) = 0, что приводит как к уравнению (14), так и к правилу для оценки σi2, т.е.
Это правило является на удивление интуитивно понятным и имеет важное значение, т.к. снижает чувствительность процесса обучения к областям со слишком редкими данными. Отметим, что этот вывод также можно понимать, как минимизацию расстояния Кульбака-Лейблера 
относительно βi и σi2, что аналогично точке зрения взвешенной регрессии. Полный алгоритм показан в листинге:
D. Перспектива будущей работы: использование метрик на основе инерции без матрицы масс
Чтобы обучить несколько важных законов управления, известных из аналитической робототехники, например, Законы управления Хатиба-Гаусса [1] и Hsu-IDM [2], наш алгоритм обучения должен быть изменён, чтобы иметь возможность вычислять соответствующие награды. В разделе II-C предположили, что награда r(u,q)= exp(−uTN(q)u) может быть легко вычислена, например, для N(q)=const. Что не относится к метрике в форме N(q)=M−n(q), т.к. она требует точного определения дорогого и подверженного ошибкам тензора инерции. Поэтому, пытаясь обучить контроллер в операционном пространстве с такой метрикой, сталкиваемся с теми же трудностями с ошибками моделирования, что и аналитические подходы. Либо нужно обучать другой закон управления, который не полностью реализует интересующие свойства желаемого закона управления (например, закона управления Хатиба-Гаусса). Как бы то ни было, переформулируя задачу обучения, можно вычислить вознаграждение без явного использования тензора инерции при использовании подхода прямого-обратного моделирования, подобного [16]. Для этого переформулируем уравнение (1):
, (20)
где q ¨=gβ(q,q˙,u) – обученная прямая модель (или предсказатель), который предсказывает ускорение для заданной команды движения u на позициях суставов q и при скоростях q˙. Используя эту команду с разностью ускорения δq¨, можно определить награду для законов управления Хатиба-Гаусса и Hsu-IDM путём
rK(u) = exp (−u1T M−1 u1) = exp (−u1T δq¨), (21)
rH(u) = exp (−u1T M−2 u1) = exp (−δq¨T δq¨), (22)
соответственно. Этот подход был протестирован успешно на призматическом роботе.
III. ОЦЕНИВАНИЕ
Чтобы продемонстрировать осуществимость нашего подхода к обучению, мы оценили наш учебный контроллер в операционном пространстве на плоской руке робота с тремя степенями свободы, аналогично как в [19]. Сейчас проводится оценка антропоморфного робота-манипулятора SARCOS master со семью степенями свободы.
А. Моделируемый эксперимент
Плоский робот с тремя степенями свободы показан на рисунке 3. Связи имеют длину l1 = l2 = 35 см и l3 = 30 см. Масса звеньев определяется как m1 = m2 = m3 = 3 кг. Динамические уравнения робота, используемые в симуляторе, были автоматически получены с использованием методологии Newton-Euler.
Рис. 3. Для экспериментов с управлением следования за целью рассмотрим робота с тремя поворотными степенями свободы. Длина полностью вытянутой руки робота = 1 м.
| 
Рис. 4. На этом рисунке показаны аналитический (синяя сплошная на заднем плане) и обученный (зеленая пунктирная) контроллеры. Следование в пространстве целей обученного контроллера является совершенным. Едва ли можно отличить от аналитического оптимального решения.
|
Цель эксперимента – обучить отслеживать траектории в операционном пространстве в ограниченной части рабочего пространства (workspace), т.е. когда захват находится в прямоугольнике с длиной горизонтальной стороны 30 см, длиной вертикальной стороны 20 см и центром в х = 50 см и у = 10 см. Легко проверить, что в этом регионе динамика робота сильно нелинейная, особенно на высоких скоростях робота.
Метрика функции стоимости постоянна и определяется как:
N = diag (4.44, 1.01, 0.07), (23)
вытекает из рассуждений о том, что в наихудшем случае положение q=0, это будет близко квадрату диагонали линеаризованной матрицы масс. Кроме того, предполагаем наличие закона управления в ноль-пространстве u0 = −KDNq˙− KDN(q − qrest), тянущего робота в положение покоя:
qrest = [−1.2366, 1.64, 0.95485]T, (24)
которое соответствует позиции в пространстве сочленений, приближающее захват к центру рассматриваемого рабочего пространства. Усилия (gains) компоненты ноль-пространства определяются как KDN= diag (20, 6, 2) и KPN= diag (0.5, 0.3, 0.1). Обратите внимание, что этот член в ноль-пространстве соответствует упругости (пружине, spring) в пространстве сочленений, которая в большинстве случаев растягивается из-за ограничений задачи (constraints), следовательно, более низкий коэффициент усилия KPN.
B. Результаты
Эксперимент состоит из двух фаз. В первой фазе закон управления обучается с использованием данных, сгенерированных другой политикой, во второй фазе обученный закон управления используется для генерации большего количества данных. В первой фазе сгенерирована последовательность из 200 произвольных положений в пространстве сочленений, для которых захват находился в желаемом прямоугольнике рабочей области, затем эти позиции были соединены в пространстве сочленений с помощью полиномов пятого порядка, чтобы создать желаемые траектории в пространстве сочленений продолжительностью 1 с. Для генерации данных использовался преднамеренно плохо настроенный закон PD-контроллер, который не мог точно отслеживать траектории. Эти данные были добавлены в систему обучения, и был изучен первый закон управления в операционном пространстве. Впоследствии изученный закон управления был протестирован на эталонной траектории восьмерки длитель