Делитель частоты - устройство, которое при подаче на его вход периодической импульсной последовательности формирует на выходе такую же последовательность, но имеющую частоту повторения импульсов, в определенное число раз меньшую, чем частота повторения импульсов входной последовательности.
Отличие делителей частоты от счетчиков состоит в следующем. В счетчике каждая комбинация состояний триггеров определяет в некоторой системе счисления число импульсов, поступивших к данному моменту времени. В делителе частоты последовательность состояний может быть выбрана произвольной, важно лишь обеспечить заданный период цикла N. Последовательность состояний выбирается из соображений обеспечения при заданном N наибольшей простоты межтриггерных связей. Эти связи должны выполняться непосредственным соединением выходов одних триггеров со входами других без использования логических элементов. Счетчик, имеющий то же значение N, может выполнять роль делителя частоты, однако следует иметь в виду, что такое решение будет неэкономичным.
Рассмотрим схемы делителей частоты с различными коэффициентами деления N.

рис 8.54
Делитель частоты с коэффициентом деления N = 2. Схема делителя приведена на рис. 8.54,а. В моменты отрицательного фронта входных импульсов триггер переключается в новое состояние. Как видно из временной диаграммы на рис. 8.54,а, период импульсной последовательности Твых на выходе триггера оказывается вдвое больше периода Твх следования импульсов на входе. Следовательно, fвых = 1/Tвых = 1/(2Tвх) = fвx/2, т. е. частота следования импульсов на выходе в 2 раза ниже, чем на входе.
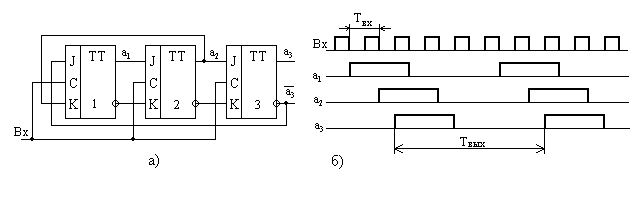
рис 8.55
Делители частоты с коэффициентом деления N = 2n. На рис. 8.42,а показано последовательное соединение делителей частоты с коэффициентом деления, равным двум, при котором выход каждого из делителей подключен к входу следующего. На выходе каждого делителя частота следования импульсов вдвое ниже, чем на входе. Так, если частота следования импульсов на входе первого делителя fвх, то на выходе первого делителя она равна fвых1 = fвх/2, на выходе второго fвых2 = fвых1/2 = fвх/22, на выходе третьего делителя fвых3 = fвых2/2 = fвх/23 и т. д. При n каскадах подобного деления частота выходной последовательности окажется равной fвых = fвх/2n, т. е. будет осуществляться деление частоты в N = 2n раз.
| Таблица 8.32 | ||||||
| Номер входного импульса | Состояние триггеров | |||||
| текущее | следующее | |||||
| a3 | a2 | a1 | a3 | a2 | a1 | |
| ... | ... | ... | ... | ... | ... | ... |
| Таблица 8.33 | ||||||
| Номер входного импульса | Состояние триггеров | |||||
| текущее | следующее | |||||
| a3 | a2 | a1 | a3 | a2 | a1 | |
| ... | ... | ... | ... | ... | ... | ... |
Делитель частоты с коэффициентом деления N = 3. Счетчик с периодом цикла N = 3 имеет простейшие межтриггерные связи без использования логических элементов. Этот счетчик может одновременно служить и делителем частоты с коэффициентом N = 2.
Делитель частоты с коэффициентом деления N = 5. Схема делителя и временная диаграмма работы приведены на рис. 8.55, а таблица состояний - в табл. 8.32. Как видно из временной диаграммы, на выходах всех триггеров образуется последовательность импульсов с частотой, в 5 раз более низкой, чем частота импульсов на входе делителя.
Делитель частоты с коэффициентом деления N = 7. На рис. 8.56 приведены схема делителя и временная диаграмма его работы, в табл. 8.33 - таблица состояний.
Каскадные делители частоты. В тех случаях, когда коэффициент деления N не является простым числом и может быть представлен произведением вида N = Nl . N2 . N3 .... . Nk, схема делителя строится в виде каскадного соединения делителей, имеющих коэффициенты деления N1, N2, N3,..., Nk (рис. 8.57).

| |
| рис 8.57 | рис 8.58 |

рис 8.56
Примером такого каскадного построения делителей является рассмотренный ранее делитель с коэффициентом 2n (см. рис. 8.54).
Построим делитель с коэффициентом деления N = 6. Этот коэффициент можно представить произведением N = 3 . 2. Таким образом, данный делитель может быть построен в виде каскадного соединения делителей, имеющих коэффициенты деления N1 = 2 и N2 = 2. Схема делителя показана на рис. 8.58.

рис 8.59

рис 8.60
Рассмотрим построение делителя с коэффициентом деления N = 9. Этот коэффициент может быть представлен в форме N = 3 . 3 и реализован каскадным соединением двух делителей с коэффициентами N1 = N2 = 3 (рис. 8.59).
Рассмотрим еще пример: построим делитель с коэффициентом N = l0. Представим N = N1 . N2 = 5 . 2, при этом схема делителя строится в виде каскадного соединения делителей с коэффициентами Nl = 5 и N2 = 2, как показано на рис. 8.60.
Таким образом, имея набор схем, реализующих коэффициенты деления, которые представляют собой простые числа, можно каскадным их соединением получать делители с разнообразными коэффициентами деления.