1.1 Что такое игра в нормальной форме? Что такое строго доминируемая стратегия для игры в нормальной форме? Что такое равновесие Нэша в игре в нормальной форме?
1.2 Какие стратегии останутся при последовательном исключении доминируемых стратегий в данной игре в нормальной форме? Каковы равновесия Нэша (в чистых стратегиях) в этой игре?
| L | C | R | |
| T | 2, 0 | 1, 1 | 4, 2 |
| M | 3, 4 | 1, 2 | 2, 3 |
| B | 1, 3 | 0, 2 | 3, 0 |
1.3 Игроки 1 и 2 ведут переговоры по дележу общего подарка стоимостью 1. Оба игрока одновременно называют желаемые доли s1 и s2 от 0 до 1. Если их сумма s1+s2 не больше 1, то они получают желаемое. Если s1+s2 > 1, то они не получают ничего (т.е. по 0). Каковы равновесия Нэша (в чистых стратегиях) в этой игре?
1.4 Предположим, что в модели олигополии Курно – n фирм. Пусть qi – объем выпуска фирмы i, а совокупный выпуск равен Q = q1+...+qn. Пусть P – рыночная цена, соответствующая данному объему выпуска, определяется обратной функцией спроса P(Q) = a – Q (при Q < a, иначе P = 0). Предположим, что полные затраты фирмы i по выпуску qi равны Сi(qi)=c qi, т.е. что нет фиксированных затрат (не зависящих от объема выпуска) и что предельные затраты (на единицу выпуска) постоянны и равны c < a. Будем считать, что фирмы выбирают объемы выпуска одновременно. Каково равновесие по Нэшу? Что будет при n, стремящимся к бесконечности?
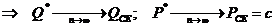 |
1.5 Рассмотрим две конечные версии модели дуаполии Курно. В первой версии будем считать, что каждая фирма должна выбрать между половиной монопольного выпуска qm/2 = (a – c)/4 или равновесным по Нэшу объемом
qc/2 = (a – c)/3. Другие объемы выпуска невозможны. Покажите, что получившаяся игра эквивалентна дилемме заключенного: у каждого игрока есть строго доминирующая стратегия, но равновесие хуже для обоих, чем кооперативный исход. Во второй версии будем считать, что каждая фирма может выбрать один из трех объемов выпуска: qm/2, qc или q’. Найдите такое значение q’, чтобы эта игра была бы эквивалентна модели Курно в том смысле, что единственным равновесием Нэша в ней было бы (qc, qc).
|
|
1.6 Рассмотрим дуаполию Курно с обратной функцией спроса P(Q) = a – Q, но с асимметричными затратами: c1 и c2. Каково равновесие Нэша при условии
0 < ci < a/2 для каждой фирмы? А что, если c1 < c2 < a, но 2c2 > a + c1?
1.7 Предположим, что в модели Бертрана фирмы выпускают однородный продукт и могут полностью удовлетворить весь спрос. Точнее, будем считать что спрос для фирмы i равен a – pi, если pi < pj, 0, если pi > pj и
(a – pi)/2, если pi = pj. Предположим, что нет фиксированных и что предельные затраты (на единицу выпуска) постоянны и равны c < a. Покажите, что если фирмы выбирают цены одновременно, то в единственном равновесии Нэша они выберут цену с.
1.8 Предположим, что мнения некоторого электората равномерно распределены по идеологическому спектру от левого фланга (х = 0), до правого (х = 1). Каждый кандидат в рамках предвыборной кампании выбирает свою платформу (точку на отрезке [0,1]). Каждый избиратель видит все платформы кандидатов и голосует за кандидата с наиболее близкой для себя платформой. Например, если всего участвуют два кандидата с платформами
х1 = 0.3, х2 = 0.6, то за первого проголосуют с мнениями из отрезка [0,0.45], а за второго – из отрезка [0.45,1], поэтому победит второй (55% против 45%). Предположим, что для кандидатов главное быть избранными, а суть платформы для них не совсем важна. Каково равновесие Нэша в случае двух кандидатов? Каково равновесие Нэша при трех и более кандидатов? (Предположим, что кандидаты, выдвинувшие одну платформу делят голоса, а если победителей несколько, то между ними бросается жребий)
|
|
1.9 Что такое смешанная стратегия для игры в нормальной форме? Что такое равновесие по Нэшу в смешанных стратегиях?
1.10 Покажите, что в следующих двух играх нет новых равновесий Нэша в смешанных стратегиях (кроме равновесий в чистых стратегиях).
| Дилемма заключенного | Заключенный 2 | ||
| молчать | сознаться | ||
| Заключенный 1 | молчать | –1, –1 | –9, 0 |
| сознаться | 0, –9 | –6, –6 |
| L | C | R | |
| T | 0, 4 | 4, 0 | 5, 3 |
| M | 4, 0 | 0, 4 | 5, 3 |
| B | 3, 5 | 3, 5 | 6,6 |
1.11 Найдите равновесия по Нэшу в смешанных стратегиях для игры из задачи 1.2.
1.12 Найдите равновесие Нэша в смешанных стратегиях в следующей игре в нормальной форме.
| L | R | |
| T | 2, 1 | 0, 2 |
| B | 1, 2 | 3, 0 |
1.13 У каждой из двух фирм есть по одной вакансии на однотипную работу. Предположим, что они предлагают разную зарплату: фирма i предлагает зарплату wi, причем (1/2)w1 < w2 < 2w1. Предположим, что есть два рабочих, которые могут одновременно подать заявку, причем только в одну фирму. Если они подали заявки в разные фирмы, то оба получают работу. Если они подали заявки в одну и ту же фирму, то кто-то один из них (по жребию) получает работу, а другой остается без работы. Найдите равновесия Нэша в этой игре:
| Рабочий 2 | |||
| заявка в фирму 1 | заявка в фирму 2 | ||
| Рабочий 1 | заявка в фирму 1 | w1/2,w1/2 | w1,w2 |
| заявка в фирму 2 | w2,w1 | w2/2,w2/2 |
1.14 Докажите, что чистые стратегии, входящие с положительной вероятностью в равновесие Нэша в смешанных стратегиях сохранятся при последовательном исключении строго доминируемых стратегий.