Линейные пространства
Задание 1. Образует ли линейное пространство заданное множество, в котором определены сумма любых двух элементов a и b и произведение любого элемента а на любое число a?
1.1. Множество всех действительных чисел;
сумма a + b, произведение a*a.
Решение. Проверяем замкнутость множества действительных чисел относительно введенных операций суммы элементов множества и произведения элемента множества на число. Сумма действительных чисел и произведение действительного числа на любое число являются действительными числами. То есть операции a + b и a*a определены на заданном множестве. Аксиомы линейного пространства 1)-8) выполняются на основании правил арифметических операции. Нулевым элементом является число 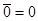 , а противоположным для числа а является число (- а), так как
, а противоположным для числа а является число (- а), так как
а +(- а)=0.
Ответ. Множество действительных чисел с введенными операциями суммы элементов множества и произведения элемента множества на число является линейным пространством.
1.2. Множество всех симметрических матриц  ,
,  ,
,  ,
,  ,
,  ; сумма
; сумма  , произведение
, произведение  .
.
Решение. Проверяем замкнутость множества симметричных матриц относительно введенных операций суммы элементов множества и произведения элемента множества на число. Сумма симметричных матриц и произведение симметричной матрицы на число являются симметричными матрицами. То есть операции a + b и a*a определены на заданном множестве. Аксиомы линейного пространства 1)-8) выполняются на основании свойств линейных операции над матрицами. Нулевым элементом является матрица  ,
,  , а противоположным элементом -
, а противоположным элементом -  .
.
Ответ. Множество симметрических матриц с введенными операциями суммы матриц и произведения матрицы на число является линейным пространством.
Задание 2. Найти какую-либо базу системы векторов и выразить через нее все векторы системы.

Решение. Составим матрицу, столбцами которой являются координаты заданных векторов и приведем ее к упрощенному виду с помощью элементарных преобразований строк:
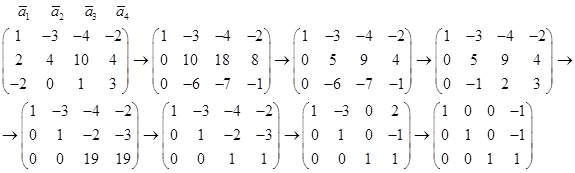
В полученной матрице столбцы, являющиеся столбцами единичной матрицы линейно независимы, а остальные столбцы являются линейной комбинацией этих столбцов. Отсюда векторы, соответствующие столбцам единичной матрицы линейно независимы, а остальные векторы являются линейной комбинацией этих векторов. Таки образом, векторы 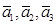 линейно независимы и составляют базу исходной системы, а вектор
линейно независимы и составляют базу исходной системы, а вектор  является линейной комбинацией этих векторов. Из упрощенной матрицы записываем выражение четвертого столбца через первые три
является линейной комбинацией этих векторов. Из упрощенной матрицы записываем выражение четвертого столбца через первые три

Следовательно, четвертый вектор  является линейной комбинацией векторов
является линейной комбинацией векторов 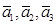 с теми же коэффициентами, то есть
с теми же коэффициентами, то есть
 .
.
Ответ:
а) база системы: векторы 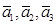 ,
,
б) выражение векторов через векторы базы:
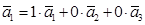 ,
,  ,
,
 ,
,  .
.
Задание 3. В линейном пространстве  задан базис
задан базис  . Заданы разложения векторов
. Заданы разложения векторов  по базису
по базису  и задан
и задан  - столбец координат вектора
- столбец координат вектора  в базисе
в базисе  и
и  - столбец координат вектора
- столбец координат вектора  в базисе
в базисе  .
.
1. Доказать, что система векторов  является базисом пространства
является базисом пространства  .
.
2. Записать матрицу перехода от базиса  к базису
к базису  и матрицу перехода от базиса
и матрицу перехода от базиса  к базису
к базису  .
.
3. Найти разложение вектора  по базису
по базису  и разложение вектора
и разложение вектора  по базису
по базису  .
.
4. Записать  - столбец координат вектора
- столбец координат вектора  в базисе
в базисе  и
и  - столбец координат вектора
- столбец координат вектора  в базисе
в базисе  .
.
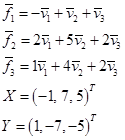
Решение. Запишем координаты векторов  в базисе
в базисе 
 .
.
Чтобы доказать, что система векторов  является базисом, надо доказать их линейную независимость. Для этого составим матрицу, столбцами которой являются координаты векторов
является базисом, надо доказать их линейную независимость. Для этого составим матрицу, столбцами которой являются координаты векторов  в базисе
в базисе  и вычислим ее ранг.
и вычислим ее ранг.

Ранг матрицы равен трем, значит система векторов  линейно независима и является базисом пространства.
линейно независима и является базисом пространства.
Записанная выше матрица является матрицей перехода от базиса  к базису
к базису  , то есть
, то есть
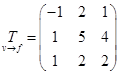 .
.
Матрица перехода от базиса  к базису
к базису  является обратной к матрице
является обратной к матрице  , то есть
, то есть  . Вычислим ее
. Вычислим ее

Таким образом получили

Теперь можно вычислить столбец координат вектора  в базисе
в базисе 

истолбец координат вектора  в базисе
в базисе 

Разложения векторов запишутся в виде
 ,
,

Ответ:
1. Система векторов  является базисом пространства
является базисом пространства  .
.
2. Матрицы перехода
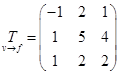 ,
,  .
.
3. Разложения векторов
 ,
,

4. Столбцы координат векторов
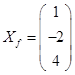 ,
,  .
.
Задание 4. В линейном пространстве  задан базис
задан базис 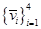 и заданы координаты векторов
и заданы координаты векторов 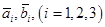 в этом базисе
в этом базисе
- Найти базисы подпространств
 ,
,  ,
,
 ,
,  .
.
- Убедиться в справедливости равенства
 .
.
 :
: 
 :
: 
Решение.
Для того, чтобы найти базисы подпространств, заданных своими оболочками, необходимо выделить в каждой из оболочек выделить максимальную линейно независимую подсистему, которая и является базисом подпространства. Для этого составляем матрицу по столбцам из векторов данной системы и приведем ее к ступенчатому виду элементарными преобразованиями.
Подпространство  :
:

Ранг этой матрицы равен 3, и значит, что векторы  линейно независимы являются базисом подпространства
линейно независимы являются базисом подпространства  . Размерность подпространства
. Размерность подпространства  равна
равна 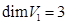 .
.
Подпространство  :
:

Ранг этой матрицы равен 3, и значит, что векторы  линейно независимы являются базисом подпространства
линейно независимы являются базисом подпространства  . Размерность подпространства
. Размерность подпространства  равна
равна  .
.
Сумма подпространств  .
.
Сумма подпространств  и
и  определяется линейной оболочкой векторов, задающих эти подпространства
определяется линейной оболочкой векторов, задающих эти подпространства
 .
.
Базис и размерность этого подпространства ищем аналогично предыдущему. Для этого составляем матрицу, построенную из векторов  по столбцам, и приведем ее к ступенчатому виду элементарными преобразованиями.
по столбцам, и приведем ее к ступенчатому виду элементарными преобразованиями.

Ранг этой матрицы равен 4, и значит, что векторы  линейно независимы и являются базисом суммы подпространств
линейно независимы и являются базисом суммы подпространств  . Размерность суммы подпространств
. Размерность суммы подпространств  равна
равна 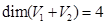 .
.
Пересечение подпространств  .
.
Из определения пересечения подпространств

следует, что если  то его можно представить в виде разложения по базису подпространства
то его можно представить в виде разложения по базису подпространства 
 ,
,
а если  то его можно представить в виде разложения по базису подпространства
то его можно представить в виде разложения по базису подпространства 
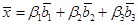
То есть

Правая часть этого равенства представляет собой однородную систему линейных алгебраических уравнений относительно неизвестных коэффициентов  :
:
 ,
,
или

Найдем ее фундаментальную совокупность решений, приведя матрицу системы к упрощенному виду


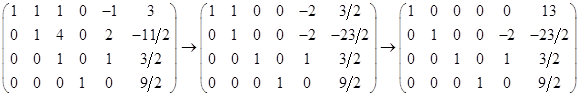
Ранг этой системы равен r =2, а число неизвестных n=6. Значит фундаментальная совокупность решений будет состоять из n-r =2 решений. Найдем эти решения приняв за свободные неизвестные  :
:

Получили, что набору значений  (а также набору
(а также набору  ) соответствует вектор
) соответствует вектор  , набору
, набору  (а также набору
(а также набору 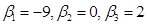 ) соответствует вектор
) соответствует вектор  . Эти векторы линейно независимы и, как следует из определения фундаментальной совокупности решений, через них линейно выражаются все решения системы. Следовательно, векторы
. Эти векторы линейно независимы и, как следует из определения фундаментальной совокупности решений, через них линейно выражаются все решения системы. Следовательно, векторы  являются базисом пересечения подпространств
являются базисом пересечения подпространств  и
и  .
.
Проверяем равенство  : 3+3=4+2.
: 3+3=4+2.
Ответ.
1. Базис подпространства  : векторы
: векторы  ,
,  ,
,
2. Базис подпространства  : векторы
: векторы  ,
,  ,
,
3. Базис суммы подпространств  : векторы
: векторы  ,
,  ,
,
4. Базис пересечения подпространства  : векторы
: векторы 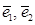 ,
,  .
.
Задание 5. Найти базисы и размерности суммы и пересечения подпространств  и
и  :
:  ,
,  , если подпространства заданы как множества решений однородных систем линейных уравнений, где:
, если подпространства заданы как множества решений однородных систем линейных уравнений, где:
 :
: 
Решение.
Базисом подпространства, заданного однородной системой линейных уравнений, является фундаментальная совокупность решений этой системы. Фундаментальную совокупность будем искать приведением матрицы системы к упрощенному виду элементарными преобразованиями.
Подпространство  .
. 


Число неизвестных n равно 4, а ранг матрицы  равен 2. Следовательно, размерность подпространства решений равна
равен 2. Следовательно, размерность подпространства решений равна 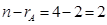 . В качестве свободных неизвестных выбираем
. В качестве свободных неизвестных выбираем 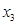 и
и  . Чтобы избежать дробных чисел, придадим свободным неизвестным сначала значения
. Чтобы избежать дробных чисел, придадим свободным неизвестным сначала значения  , а затем
, а затем  и вычислим значения главных неизвестных
и вычислим значения главных неизвестных 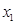 и
и  .
.
 .
.
В итоге получаем два вектора  и
и 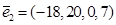 , которые являются базисом подпространства
, которые являются базисом подпространства  . Размерность этого подпространства
. Размерность этого подпространства  .
.
Подпространство  .
.  ,
, 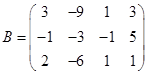

Число неизвестных n равно 4, а ранг матрицы  равен 3. Следовательно, размерность подпространства решений равна
равен 3. Следовательно, размерность подпространства решений равна  . В качестве свободного неизвестного выбираем
. В качестве свободного неизвестного выбираем  . Чтобы избежать дробных чисел, придадим свободному неизвестному значение
. Чтобы избежать дробных чисел, придадим свободному неизвестному значение  и вычислим значения главных неизвестных
и вычислим значения главных неизвестных 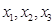
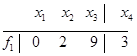
.
В итоге получаем один вектор  , который является базисом подпространства
, который является базисом подпространства  . Размерность этого подпространства
. Размерность этого подпространства  .
.
Сумма подпространств  .
.
Сумму подпространств удобнее искать исходя из описания подпространств линейными оболочками. Так как нам известны базисы подпространств, то эти подпространства можно описать линейными оболочками базисных векторов:  . Тогда сумма подпространств запишется в виде
. Тогда сумма подпространств запишется в виде  .
.
Вычислим базис суммы подпространств, выделив из системы векторов  максимальную линейно независимую систему
максимальную линейно независимую систему

Ранг этой матрицы равен 3 и значит векторы 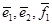 линейно независимы и являются базисом суммы подпространств
линейно независимы и являются базисом суммы подпространств  . Размерность суммы подпространств
. Размерность суммы подпространств  .
.
Пересечение подпространств  .
.
Вектор  принадлежит пересечению
принадлежит пересечению  в том случае, если он удовлетворяет обеим системам, описывающим подпространства
в том случае, если он удовлетворяет обеим системам, описывающим подпространства

Базисом пересечения  будет фундаментальная совокупность решений этой системы. Приведем матрицу к простейшему виду:
будет фундаментальная совокупность решений этой системы. Приведем матрицу к простейшему виду:

Получили, что ранг матрицы равен числу неизвестных и, следовательно, система имеет только тривиальное решение  . Значит
. Значит  и
и  .
.
Проверим соотношение для размерностей подпространств
 : 2+1=3+0.
: 2+1=3+0.
Ответ.
1. Базис подпространства  : векторы
: векторы 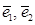 ,
,  ,
,
2. Базис подпространства  : векторы
: векторы  ,
,  ,
,
3. Базис суммы подпространств  : векторы
: векторы  ,
,  ,
,
4. Подпространства  и
и  не пересекаются:
не пересекаются:  ,
,  .
.
Задание 6. Найти базис и размерность пересечения подпространств  и
и  :
:  ,
,  , если одно из подпространств задано как множества решений однородной системы линейных уравнений, а другое подпространство задано линейной оболочкой векторов:
, если одно из подпространств задано как множества решений однородной системы линейных уравнений, а другое подпространство задано линейной оболочкой векторов:
 ,
,  ,
, 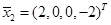 ,
,  ,
,
 :
: 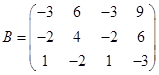
Решение.
Подпространство  .
.
Составляем матрицу по столбцам из векторов данной системы и приводим ее к ступенчатому виду элементарными преобразованиями.
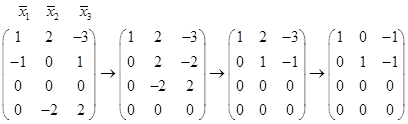
Ранг матрицы равен 2 и, значит, в матрице имеются два линейно независимых столбца. Первые два столбца линейно независимы, следовательно соответствующие им векторы  также линейно независимы и их можно принять в качестве базиса подпространства
также линейно независимы и их можно принять в качестве базиса подпространства  :
:  .
.  .
.
Подпространство  ,
,  .
.
Базисом подпространства, заданного однородной системой линейных уравнений, является фундаментальная совокупность решений этой системы. Фундаментальную совокупность будем искать приведением матрицы системы к упрощенному виду элементарными преобразованиями.

Число неизвестных n равно 4, а ранг матрицы  равен 1. Следовательно, размерность подпространства решений равна
равен 1. Следовательно, размерность подпространства решений равна  . В качестве свободных неизвестных выбираем
. В качестве свободных неизвестных выбираем  и вычисляем значения главной неизвестной
и вычисляем значения главной неизвестной  .
.

В итоге получаем три вектора  ,
,  ,
,  которые являются базисом подпространства
которые являются базисом подпространства  . Размерность этого подпространства
. Размерность этого подпространства  .
.
Сумма подпространств  .
.
Так как нам известны базисы подпространств, то эти подпространства можно описать линейными оболочками базисных векторов: 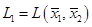 ,
,  . Тогда сумма подпространств запишется в виде
. Тогда сумма подпространств запишется в виде  . Вычислим базис суммы подпространств, выделив из системы векторов
. Вычислим базис суммы подпространств, выделив из системы векторов  максимальную линейно независимую систему
максимальную линейно независимую систему

В этой матрице первые четыре столбца линейно независимы, следовательно, соответствующие им векторы  также линейно независимы и могут быть приняты в качестве базиса суммы подпространств
также линейно независимы и могут быть приняты в качестве базиса суммы подпространств  .
.
Пересечение подпространств  .
.
Пересечение подпространств удобнее искать в том случае, когда подпространства заданы системами уравнений. Поэтому опишем подпространство  системой уравнений
системой уравнений  . Так как векторы
. Так как векторы  являются базисом
являются базисом  , то они линейно независимы и составляют фундаментальную совокупность решений искомой системы
, то они линейно независимы и составляют фундаментальную совокупность решений искомой системы  . Составим матрицу из столбцов координат векторов
. Составим матрицу из столбцов координат векторов  .
.

Из линейной независимости столбцов матрицы следует

То есть  ,
, 
Вектор  принадлежит пересечению
принадлежит пересечению 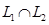 в том случае, если он удовлетворяет обеим системам, описывающим подпространства
в том случае, если он удовлетворяет обеим системам, описывающим подпространства
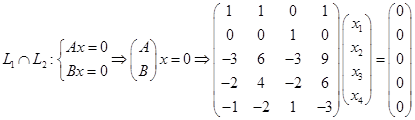
Базисом пересечения  будет фундаментальная совокупность решений этой системы. Приведем матрицу к простейшему виду:
будет фундаментальная совокупность решений этой системы. Приведем матрицу к простейшему виду:
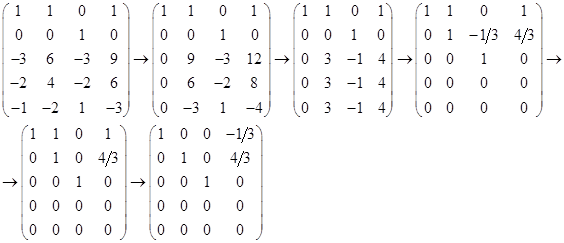
Число неизвестных n равно 4, а ранг матрицы  равен 3. Следовательно, размерность подпространства решений равна
равен 3. Следовательно, размерность подпространства решений равна  . В качестве свободного неизвестного выбираем
. В качестве свободного неизвестного выбираем  . и вычислим значения главных неизвестных
. и вычислим значения главных неизвестных 

Таким образом базисом пересечения  является вектор
является вектор  .
.
Проверим соотношение для размерностей подпространств:
 , 2+3=4+1.
, 2+3=4+1.
Ответ.
1. Базис подпространства 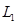 : векторы
: векторы  ,
,  ,
,
2. Базис подпространства  : векторы
: векторы  ,
,  ,
,
3. Базис суммы подпространств  : векторы
: векторы 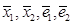 ,
,  ,
,
4. Базис пересечения подпространств 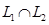 : вектор
: вектор  ,
,  .
.
Список литературы
1. Ильин В.А.,_Ким Г.Д. Линейная алгебра и аналитическая геометрия. Учебник.-М.:Изд-во Моск. Ун-та, 1998.
2. Ким Г.Д., Крицков Л.В. Алгебра и аналитическая геометрия: Теоремы и задачи. Том II, часть 1. М.:ИКД ”Зерцало”, 2003.
3. Бутузов В.Ф., Крутицкая Н.Ч., Шишкин А.А. Линейная алгебра в вопросах и задачах: Учебное пособие/ Под ред.В.Ф.Бутузова. – М.: ФИЗМАТЛИТ, 2002.
4. Бортаковский А.С. Линейная алгебра в примерах и задачах: Учеб.пособие/А.С. Бортаовский, А.В. Пантелеев. – М.:Высш.шк., 2005.
5. Проскуряков И.В. Сборник задач по линейной алгебре. – М.:Наука, 1978.
6. Воеводин В.В. Линейная алгебра. – М.: Наука, 1974.