Цель работы: э кспериментальное подтверждение теоретического обоснования устойчивости САУ.
В общем случае устойчивостью системы называется ее способность возвращаться в исходное состояние после прекращения внешнего возмущающего воздействия, которое вывело эту систему из исходного состояния.
Известно, что переход системы из одного устойчивого состояния в другое под влиянием внешнего воздействия описывается уравнениями динамики. Наглядное представление процесса смены состояний системы можно получить, наблюдая переходную характеристику на экране осциллографа (см. лабораторную работу № 2). Для устойчивых систем переход из одного состояния в другое может носить монотонный (1), апериодический (2) либо затухающий колебательный характер (3) (рис. 4.1). В неустойчивых системах переходный процесс обычно приобретает характер незатухающих колебаний.
Рис. 4.1. Различные виды переходных процессов
|
Устойчивость систем обычно определяют по критериям устойчивости, в частности по критерию Гурвица. Это алгебраический критерий, при использовании которого об устойчивости систем судят по коэффициентам характеристических уравнений. Для уравнений 1-й и 2-й степени условие устойчивости определяется положительностью всех коэффициентов. Для уравнений 3-й степени, кроме положительности всех коэффициентов, необходимо, чтобы определитель Гурвица 2-го порядка был больше 0. Примером такой системы могут служить последовательно соединенные инерционное и колебательное звенья охваченные отрицательной обратной связью (рис. 4.2).
Рис. 4.2. Структурная схема исследуемой модели
Для получения переходной характеристики необходимо собрать схему, показанную на рис. 4.3.
Рис. 4.3. Структурная схема получения
переходной характеристики
Изменяя параметры модели К, получим переходные характеристику, по форме которых будем судить об устойчивости системы. Результаты занесем в табл 4.1.
Таблица 4.1
| № п/п | K1 | K2 | K3 | K4 | Характер переходного процесса | Устойчивость системы |
Задание
1. Построить модель исследуемой системы.
2. Снять переходные характеристики при различных параметрах модели К1 ÷ К4. Занести результаты в табл. 4.1.
3. Вывести выражение передаточной функции системы. Провести анализ полученных результатов и определить условия устойчивости системы по критерию Гурвица, используя средства MATLAB.
4. Сравнить экспериментальные данные с расчетными.
Контрольные вопросы
1. Дать определение устойчивости системы.
2. Сформулировать критерий устойчивости Гурвица. Каковы его недостатки?
3. Что называется запасом устойчивости по амплитуде и фазе? Как определить эти параметры по частотным характеристикам системы?
4. Как определить устойчивость системы по виду ее АЧХ?
5. Позволяет ли вид переходной характеристики судить об устойчивости системы?
Лабораторная работа № 5
Исследование П -, И -, ПИ - регуляторов
Цель работы: изучение влияния различных типов регуляторов на характер переходного процесса в системе.
В качестве объекта управления выберем систему (колебательное звено) с передаточной функцией 
. Структурная схема объекта с такой передаточной функцией будет иметь вид, показанный на рис. 5.1.
Рис. 5.1. Структурная схема модели колебательного звена
|
Модель системы с регулятором в общем виде показана на рис. 5.2.
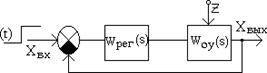Рис. 5.2. Структурная схема модели системы с регулятором
|
Основной целью использования регуляторов является уменьшение статической погрешности. Кроме того, подбирая параметры регуляторов, можно улучшить показатели переходного процесса – время регулирования и перерегулирование.
Основные параметры, характеризующие переходной процесс, показаны на рис. 5.3.
Рис. 5.3. Параметры переходного процесса
|
Статическая погрешность eст представляет собой разность между сигналом, подаваемым на вход системы, и сигналом, установившемся на ее выходе после окончания переходного процесса.
Время регулирования tp – это время, в течение которого кривая переходного процесса входит в пределы, определяющие точность регулирования. Эти пределы устанавливаются разработчиком системы. В данной работе точность регулирования, т. е. максимально допустимое отклонение кривой переходного процесса следует задавать не менее ±5 % от установившегося значения. Таким образом, можно считать, что переходной процесс закончился после того, как кривая перестала выходить из заданного диапазона.
Перерегулирование s — это максимальное отклонение переходной характеристики от установившегося значения: 
%.
Схема набора аналогична показанной в работе № 4 (см. рис. 4.3).
Сначала исследуется система без регулятора, структурная схема которой представлена на рис. 5.1. Необходимо определить параметры переходной характеристики и занести данные в табл. 5.1. В качестве возмущающего воздействия Z нужно подать на вход сумматора отрицательное постоянное смещение от блока Constant.
Для исследования системы с П-регулятором строится модель по схеме, показанной на рис. 5.4. П-регулятор – это усилитель с передаточной фунецией W П= К П. Для нескольких значений коэффициента К п определим параметры переходного процесса и занесем результаты в таблицу.
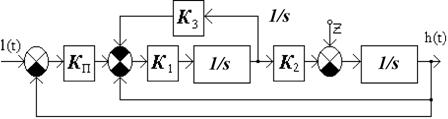
Рис. 5.4. Структурная схема модели системы с П-регулятором
Схема модели системы с И-регулятором показана на рис. 5.5.
Рис. 5.5. Структурная схема модели системы с И-регулятором
И-регулятор – это интегратор с передаточной функцией 
.
Вычислить параметры переходных процессов для нескольких значений К и и занести данные в таблицу.
Схема модели системы с ПИ-регулятором приведена на рис. 5.6.
Рис. 5.6. Структурная схема модели системы с ПИ-регулятором
ПИ-регулятор представляет собой параллельное соединение интегратора и усилителя. Его передаточная функция: 
.
Вычислить параметры переходного процесса для нескольких значений К и и К п и занести результаты в табл. 5.1.
Таблица 5.1
| Тип регулятора | Значение параметров регулирования | Х вх, В | Х уст, В | D Х, В | eст, В | Т к, мс | t р, мс | s, % | Характер переходного процесса | |
| Без регулятора | — | |||||||||
| К п= | ||||||||||
| П | К п= | |||||||||
| К п= | ||||||||||
| К и= | ||||||||||
| И | К и= | |||||||||
| К и= | ||||||||||
| К п= | К и= | |||||||||
| К и= | ||||||||||
| ПИ | К и= | |||||||||
| К п= | К и= | |||||||||
| К и= | ||||||||||
| К и= |
Задание
1. Снять переходные характеристики для различных параметров регуляторов.
2. Вычислить значения статических погрешностей и показателей качества переходного процесса.
3. Сравнить полученные результаты и сделать выводы.
Контрольные вопросы
1. Какова цель использования регуляторов в САУ?
2. Каковы основные параметры переходного процесса?
3. Как изменится время регулирования t p, если увеличить точность регулирования до ± 1 %?
4. Что называется статической погрешностью?
5. На основе проведенного анализа работы трех регуляторов выберите оптимальный.