Раздел 9. Теория теплообмена
Классификация способов передачи тепла:
1 способ:
Теплопроводность – это передача теплоты за счет обмена энергией между соседними молекулами тела. Таким образом, это микроскопический процесс (на молекулярном уровне)
2 способ:
Конвективный теплообмен. Теплота передается за счет движения молярных объемов (конечных) жидкости или газа относительно друг друга или окружающих тел.
2.1 Свободная конвекция (естественная). Движение жидкости возникает за счет разности, плотностей, которая возникает за счет разности температур.
2.2 Вынужденная конвенция. Движение жидкости происходит за счет внешней силы (насоса, вентилятора, компрессора)
3 способ:
Тепловое излучение. Энергия передается за счет электромагнитных волн.
В реальных условиях часто два или три способа осуществляется одновременно. Такой случай называют сложным теплообменом.
Раздел 10. Теплопроводность
Закон Фурье
 (12.1)
(12.1)
Функция, определяемая формулой (12.1) называется стационарным температурным полем.
 - запись температурного поля (12.2)
- запись температурного поля (12.2)
Это поле 3-х мерное нестационарное. Выражение (12.2) определяет нестационарное температурное поле t – время, х, у, z – координатные точки. Все задачи делятся на стационарные и нестационарные.
Температурный градиент

Градиент всегда направлен в сторону возрастания соответствующей величины.

Выражение (12.3 – основной закон теплопроводности – Закон Фурье)
 ,
,  – коэффициент теплопроводности
– коэффициент теплопроводности
газы: λ = 0,005¸0,05 Вт/(м×К)
жидкости: λ = 0,05¸0,7 Вт/(м×К)
металлы: λ = 10¸400Вт/(м×К)
воздух: λ = 0,024 Вт/(м×К)
вода: λ = 0,6 Вт/м×К)
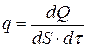 ,
,  (12.4)
(12.4)
Формула (12.4) выражает плотность теплового потока
 (12.5)
(12.5)
Формула (12.5) эквивалентна (12.3)
Дифференциальное уравнение теплопроводности
Применяя I закон термодинамики, а также закон Фурье к бесконечно-малому элементу произвольного твердого тела, можно получить следующее уравнение:
 (12.6)
(12.6)
Формула (12.6) – уравнение Пуассона, где с – теплоемкость, r – плотность
Граничные условия:
I рода: задают температуру поверхности тела Þ tпов известна;
II рода: на поверхности тела задают тепловой поток, Þ qпов;
III рода: на поверхности тела задано уравнение теплообмена

где α – коэффициент теплообмена (теплоотдачи).
Решая уравнение (12.6) совместно с граничными условиями, можно найти температурное поле любого тела.
Теплопроводность через плоскую стенку
При известных температурах t1 и t2, λ, толщине d и теплопроводности λ, требуется найти распределение температур внутри стенки, а также количество тепла, проходящее через нее. Рассмотрим стационарный случай.

Условия стационарности: 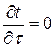
 – уравнение Лапласа
– уравнение Лапласа


 (I – интегрирование);
(I – интегрирование);
 (II – интегрирование) – общее решение.
(II – интегрирование) – общее решение.
Используя граничные условия I ряда, получим:
1.  Þ
Þ 
2. 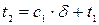 Þ
Þ  Þ
Þ 
Формула (12.7) по линейному закону описывает распределение температур по толщине стенки.
 Þ
Þ  Þ
Þ  (12.8)
(12.8)
Формула (12.8) определяет количество тепла, проходящего через стенку.
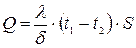 (12.9)
(12.9)
где S – площадь стенки
Формула (12.9) - выражает полное количество тепла, проходящего через стенку площади S.
Из формулы (12.8) 

Исходя из аналогии закона Фурье и закона Ома величину называют термическим сопротивлением плоской стенки.
 (12.10)
(12.10)