Найти распределение температур и количество тепла через стенку.
или
(12.11)
Выражение (12.11) – количество тепла через многослойную плоскую стенку Температуры на границах слоев определяются совместным решением уравнения (12.11) и (12.8).
Теплопроводность через цилиндрическую стенку
При заданных геометрических размерах, известных t1 и t2, λ, требуется определить распределение температур по радиусу и тепловой поток
Þ 
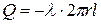
(12.12)
Проинтегрируем формулу (12.12) от внутреннего радиуса до внешнего.
t1-t2
(12.13)
Формула (12.13) выражает количество тепла через стенку трубы.
(12.14)
Выражение (12.14) определяет количество теплоты на один погонный метр трубы. Интегрируем (12.14) от внутреннего радиуса r1 текущего радиуса r.
Þ
(12.15)
Формула (12.15) выражает распределение температур по радиусу.
(12.16)
Выражение (12.16) определяет тепловой поток через многослойную цилиндрическую стенку.
Раздел 11. Конвективный теплообмен
, Вт (13.1)
Формула (13.1) выражает закон Ньютона-Рихмана,
где a – коэффициент теплоотдачи (коэффициент конвективного теплообмена), 
;
tж, tст – соответственно температура жидкости и стенки
Решение задачи конвективного теплообмена сводится к нахождению коэффициента a. В принципе эта задача сводится к составлению и решению системы дифференциальных уравнений конвективного теплообмена:
1. Уравнение теплообмена.
2. Уравнение энергии.
3. Уравнение движения жидкости (уравнение Навье-Стокса)
4. Уравнение неразрывности.
Однако эта система настолько сложна, что в настоящее время есть решения только для некоторых простых частных случаев. В этом случае на помощь приходит эксперимент. Однако, при проведении эксперимента нужно ответить на следующие вопросы:
|
|
1. Какие величины надо измерять в опыте?
2. Как их обрабатывать?
3. Как переходить от модели к натурным объектам?
На все эти вопросы отвечает теория подобия. Имеются константы подобия.
Подобие физических явлений означает, что для физических величин характеризующих эти явления, существуют константы подобия.
При этом считается, что выполняется геометрическое подобие и временное подобие.
Теоремы подобия
Теорема 1. Для подобных физических явлений существуют комплексы, составленные из величин, характеризующих эти явления, которые сохраняют одинаковое значение в сходственных точках подобных систем. Эти комплексы находят приведением дифференциальных уравнений к безразмерному виду.
Получают следующие комплексы:
1. Число Нуссельта:
где l – характерный размер данной системы;
λ – коэффициент теплопроводности жидкости
Характеризует интенсивность теплообмена на границе среда - поверхность.
2. Число Прандтля:
где 
- коэффициент кинематической вязкости;
- коэффициент температуропроводности.
Pr - определяет физические свойства теплоносителя
3. Число Грасгофа:
где 
- объемного расширения (табличные данные).
Для газов: 
где 
- термодинамическая температура газа для жидкости;
g - ускорение тяготения, 
, 
;
- температурный перепад, 
, С0
- коэффициент кинематической вязкости;
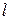- геометрический размер, м.
- зависимость между подъемной силой и силой вязкости. Характерезует свободную конвекцию.
4. Число Рейнольдca:
где – W - скорость потока жидкости или газа,
|
|
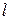- геометрический размер для трубы 
– коэффициент кинематической вязкоcти
Re определяет зависимость между 
и 
.
Теорема 2. Решение дифференциальных уравнений конвективного теплообмена может быть найдено как функция критериев подобия.
Gr, Pr, Re – определяющие критерии.
Nu – определяемый критерий.
Существует функция:
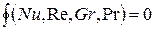
- критериальная зависимость для конвективного теплообмена.
(13.2)
(13.2) – рабочее уравнение для нахождения коэффициента a, 
где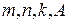 
- находится в ходе эксперимента.
Определяющие параметры:
- температура: 
- температура стенки, 
;
- температура потока жидкости, 
- средняя температура, 
- геометрический размер: для трубы – диаметр 