Реактор идеального вытеснения

Реактор идеального смешения

Непрерывного действия

 

 

Схема потоков в реакторе полного смешения представлена на рис. 1. В реакторе такого типа концентрация любого компонента равномерна по всему реакционному объему, и поэтому уравнение материального баланса можно записать для всего объема реактора. Для установившегося режима:

G_пр= G_ух+ G_хр (1),

где G_пр – масса вещества, поступающего в элементарный объем в единицу времени; G_ух - масса вещества, выходящего из элементарного объема в единицу времени; G_хр – скорость расходования исходного вещества в результате химической реакции, протекающей в элементарном объеме:

 

(2); (3). Так как степень превращения равна: (4); (5); то (6),

с0,Gv0 с, х, Gv   Рис.1. Схема реактора идеального смешения.

где, - начальная концентрация исходного вещества, - конечная концентрация исходного вещества, - объемный расход реакционной смеси, - скорость химической реакции, - время химической реакции,

-степень превращения, V - объем реакционной смеси.

Уравнение (5, 6) представляют собой проектные уравнения реактора идеального смешения и позволяют определить неизвестную величину по заданным. В любом случае для реактора идеального смешения его размер, расход реагентов, начальные и конечные концентрации могут быть определены только при условии, если известна кинетика процесса.

В таблице 1 приведены расчетные уравнения для реактора идеального смешения непрерывного действия при проведении в нем простых обратимых и необратимых, а также сложных химических реакций.

 

 

Таблица 1. Расчетные уравнения для РИС-Н

Схема реакции	Кинетическая модель	Расчетные уравнения
	при

 

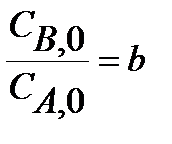
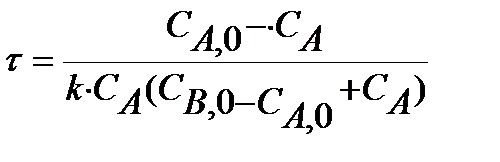
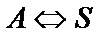
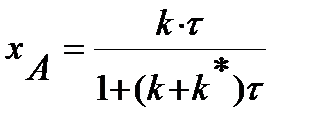
Рассмотрим некоторые примеры расчета такого типа реакторов.

Пример 1.

Определить объем реактора идеального смешения для реакции протекающего без изменения объема реакционной массы.

Дано:

реакция А → 2S;

порядок реакции n=1;

объемный расход исходного вещества G_V = 0,25 л/мин;

начальная концентрация исходного вещества С_А0= 0,5 моль/л;

константа скорости реакции k= 0.15 мин ^-1;

степень превращения x_A = 0,52.

Решение.

Так как реакция первого порядка, скорость реакции определяем по уравнению:

.

В РИС-Н приравниваем объем реакционной массы к объему реактора, тогда по уравнению:

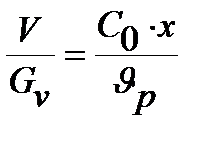
Пример 2.

Определить объем реактора идеального смешения для обратимой реакции протекающего без изменения объема реакционной массы.

Дано:

реакция 2А ↔R+S;

порядок реакции n=2;

объемный расход исходного вещества G_V = 4,8 м³/ч;

начальная концентрация исходного вещества С_А,0= 1,5 кмоль/м³;

константа скорости прямой реакции k₁ = 2*10-3 м³/(кмоль∙с);

константа равновесия Кр = 9;

требуемая степень превращения x_A = 0,8 от равновесной.

Решение.

Объем реактора, в котором проводится данная реакция, определяем из базового уравнения для РИС-Н:

; .

Так как реакция обратимая, составляем кинетическую модель для данной реакции:

т.к. и .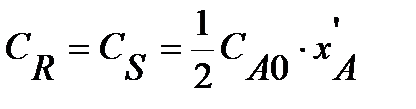

С учетом вышеизложенного выражаем время реакции:

,

где - фактическая степень превращения;

- константа скорости обратной реакции.

В этом уравнении неизвестными величинами являются фактическая степень превращения и константа скорости обратной реакции. Константу скорости обратимой реакции определяем из уравнения:

.

Для определения равновесной степени превращения используем константу равновесия, выраженную через концентрации веществ:

,

где -равновесная степень превращения.

Подставляя в данное выражение значения константы равновесия, получаем . Так как требуемая степень превращения равна 0,8, то фактическая степень превращения будет равна:

.

Тогда время реакции будет равно:

.

С учетом полученного времени реакции объем реактора составит:

Пример 3.

Определить объем реактора смешения и достигаемую степень превращения вещества А при условии, что производительность (П) по продукту R составляет 4,8 кмоль/ч.

k1 R A k2 S

Дано:

Реакция

объемный расход исходного вещества G_V = 100 л/мин.;

начальная концентрация исходного вещества С_А0= 1,6 моль/м³;

константа скорости прямой реакции k₁ = 0,28 л/(моль*мин.);

константа скорости обратной реакции k₂ = 0,12 л/(моль*мин.).

Решение.

По заданной производительности определяем концентрацию по продукту R. Для этого переведем производительность в моль/мин.

Скорость изменения концентрации продукта R в реакторе смешения можно выразить так:

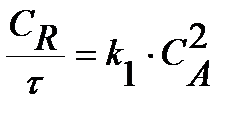или .

Из базового уравнения для РИС-Н получаем:

где ;

; следовательно,

.

 

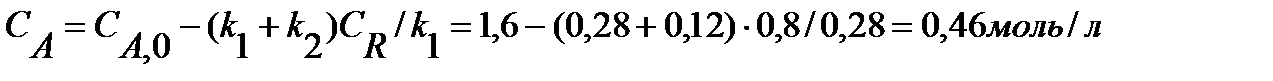Определяем степень превращения по уравнению:

.

Определяем время пребывания исходя из базового уравнения:

Определяем объем реактора:

.

Пример 4.

Рассчитать объем реактора смешения для получения максимального количества продукта R, а также определить селективность и производительность по продукту R.

Дано:

Реакция: А → R → S

объемный расход исходного вещества G_V = 18м³/ч;

начальная концентрация исходного вещества С_А0= 4,8 моль/л;

константа скорости прямой реакции k₁ = 5мин^-1 и k₂ = 1,8мин^-1.

Решение.

Для получения максимального количества продукта R необходимо выводить реакционную массу из реакционной зоны в момент, когда концентрация вещества R максимальна, что соответствует оптимальному времени пребывания в реакционной зоне.

Из базового уравнения для реактора смешения для продукта R запишем выражение:

, и при условии, что получаем выражения для определения концентрации продукта R на выходе из реактора:

.

Оптимальное время пребывания реакционной массы в зоне реакции определяем по формуле (см. таб.1).

Рассчитываем степень превращения вещества А по формуле (см. таб. 1.):

.

Определяем концентрацию R на выходе из реактора:

.

Определяем производительность по продукту R.

Рассчитываем объем реактора смешения:

.

Определяем селективность по продукту R:

.

Реактор идеального вытеснения

Реактор идеального вытеснения характеризуется тем, что любой элемент объема реагирующей среды движется по высоте (длине) реактора параллельно другим элементам, не смешиваясь с предыдущими и последующими элементами объема.

На рис. 2 схематично показана изменение степени превращения х_А, исходных концентраций С_А и других параметров в реакторе идеального вытеснения. Материальный баланс такого реактора при G_нач = 0 запишется в виде:

Gпр= Gух+ Gхр (7) (8) (9) (10)

СА,0,Gv0 СА, хА,Gv   GV + dGV хА +dхА, τ + dτ СА,0 +dСА,0 Рис.2. Схема реактора идеального вытеснения.

После подстановки значений составляющих материального баланса в уравнение (7) и преобразований получим:

(11).

Приведенное уравнение с начальным условием V=0, С_А= С_А0 для некоторых видов простых химических реакций имеет аналитическое решение. В таблице 2 приведены решения уравнения (11) как расчетные формулы для реактора, работающего в режиме идеального вытеснения при проведении в нем необратимых химических реакций, когда реакционный объем остается постоянным.

Таблица 2. Расчетные уравнения для реактора идеального вытеснения

Схема реакции	Кинетическая модель	Расчетные уравнения
	при

 

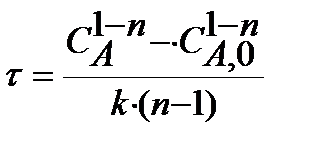
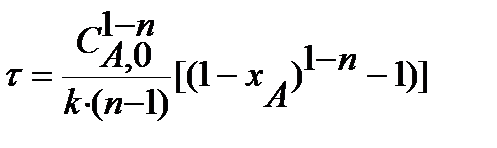
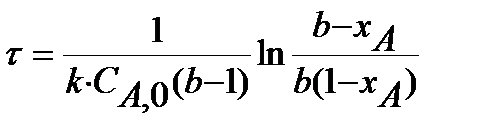
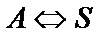
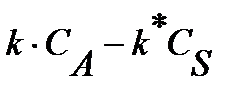
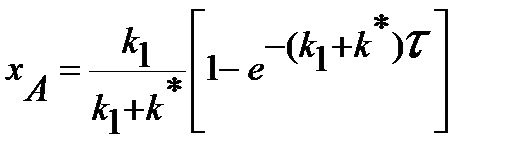
Примеры расчетов.

Пример 5.

Определить объем реактора идеального вытеснения для реакции протекающего без изменения объема реакционной массы.

Дано:

реакция А → S;

порядок реакции n=1;

объемный расход исходного вещества G_V = 30 л/мин;

начальная концентрация исходного вещества С_А0= 0,2 моль/л;

константа скорости реакции k= 0.25 мин ^-1;

степень превращения x_A = 0,82.

Решение.

По базовому уравнению РИВ определяем время реакции:

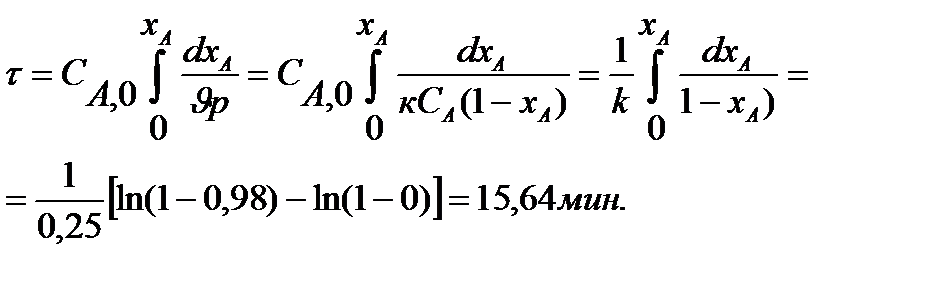
Рассчитываем объем РИВ:

; .

Пример 6.

Определить производительность реактора по продукту R рассчитать объем реактора идеального вытеснения для полученной производительности, если данная реакция проводиться в РИС-Н.

Дано:

реакция 2А → R;

порядок реакции n=2;

объемный расход исходного вещества G_V = 3,6 м³/ч;

начальная концентрация исходного вещества С_А,0= 0,5 кмоль/м³;

константа скорости реакции k= 2,3 л/(моль∙мин);

V_РИС-Н= 0,4 м³ .

Решение.

Определим время пребывания в реакторе смешения:

Из базового уравнения для реактора смешения находим

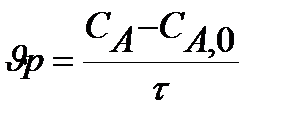, где , находим значение

Рассчитываем степень превращения вещества А:

Находим производительность по продукту R:

П_R = G₀ С_А,0 х_А /v_A =3,6∙0,5∙0,7/2=0,63кмоль/ч.

Рассчитываем время пребывания в реакторе идеального вытеснения(см. таб.2):

Определяем объем реактора вытеснения по формуле:

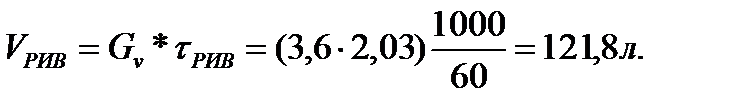
Пример 7.

Определить мольную нагрузку на реактор по веществу А и степень превращения в реакторе вытеснения.

k1 R A k2 S

Дано:

реакция

порядок реакции n=2;

объемный расход исходного вещества G_V = 6 м3/ч;

концентрация продукта R на выходе из реактора равна 2.5 кмоль/м3;

константа скорости реакции k₁= 0,3 мин^-1, k₂= 0,2мин^-1;

V_РИВ = 300 л.

Решение.

Определяем мольную нагрузку на реактор

Неизвестную начальную концентрацию вещества А на входе в реактор определяем из уравнения:

.

Находим время пребывания:

Рассчитываем начальную концентрацию вещества А:

Находим мольную нагрузку на реактор:

Определяем концентрацию вещества А на выходе из реактора исходя из базового уравнения для реактора вытеснения:

Интегрируя это уравнение и решая относительно С_А, получаем:

Рассчитываем степень превращения вещества А: