Кинематические цепи. Определение подвижности плоских кинематических цепей.
Любой механизм можно рассматривать в виде совокупности неподвижного звена и подвижных звеньев. Подвижные звенья соединяются между собой или с неподвижным звеном таким образом, что всегда есть возможность движения одного звена относительно другого.
Кинематической парой называется соединение двух звеньев, допускающее их относительное движение. Элементом кинематической пары является совокупность линий, поверхностей или отдельных точек звена, по которым происходит соприкосновение двух звеньев, образующих кинематическую пару.
Кинематическая цепь – это система звеньев, которые связаны между собой кинематическими парами. К примеру, шатун с коленчатым валом образуют между собой одну кинематическую пару, поршень с шатуном образуют другую кинематическую пару, цилиндр и поршень образуют третью кинематическую пару. Совокупность всех этих кинематических пар и называется кинематической цепью. Кинематическая цепь является основой любого механизма. Но не любая кинематическая цепь является механизмом. Назначением механизма является осуществление заранее заданных закономерных движений. Из этого можно сделать вывод, что кинематическая цепь будет механизмом только в том случае, когда звенья механизма осуществляют целесообразные движения для решения инженерных задач.
Основные механические характеристики материалов
Для количественной оценки основных свойств материалов, как
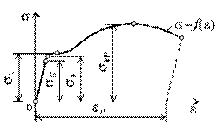 Рис. 2.9
Рис. 2.9
|
правило, экспериментально определяют диаграмму растяжения в координатах s и e(рис. 2.9), На диаграмме отмечены характерные точки. Дадим их определение.
|
|
Наибольшее напряжение, до которого материал следует закону Гука, называется пределом пропорциональности s П. В пределах закона Гука тангенс угла наклона прямой s = f (e) к оси e определяется величиной Е.
Упругие свойства материала сохраняются до напряжения s У , называемого пределом упругости. Под пределом упругости s У понимается такое наибольшее напряжение, до которого материал не получает остаточных деформаций, т.е. после полной разгрузки последняя точка диаграммы совпадает с начальной точкой 0.
Величина s Т называется пределом текучести материала. Под пределом текучести понимается то напряжение, при котором происходит рост деформаций без заметного увеличения нагрузки. Если необходимо различать предел текучести при растяжении и сжатии s Т соответственно заменяется на s ТР и s ТС . При напряжениях больших s Т в теле конструкции развиваются пластические деформации e П, которые не исчезают при снятии нагрузки.
Отношение максимальной силы, которую способен выдержать образец, к его начальной площади поперечного сечения носит название предела прочности, или временного сопротивления, и обозначается через, s ВР (при сжатии s ВС ).
| Материал | s ТР | s ТС | s ВР | s ВС | Е ×10-8 |
| Сталь | - | ||||
| Чугун | 0.7 | ||||
| Медь | - | 1.1 | |||
| Алюминий | - | 0.75 |
В табл. 2 приводятся значения указанных характеристик (в кН/м2) наиболее распространенных конструкционных материалов.
При выполнении практических расчетов реальную диаграмму (рис. 2.9) упрощают, и с этой целью применяются различные аппроксимирующие диаграммы. Для решения задач с учетом упруго-пластических свойств материалов конструкций чаще всего применяется диаграмма Прандтля. По этой диаграмме напряжение изменяется от нуля до предела текучести по закону Гука s = Е e, а далее при росте e, s = s Т (рис. 2.10).
|
|
Способность материалов получать остаточные деформации носит название пластичности. На рис. 2.9 была представлена характерная диаграмма для пластических материалов.

Рис. 2.10 Рис. 2.11
Противоположным свойству пластичности является свойство хрупкости, т.е. способность материала разрушаться без образования заметных остаточных деформаций. Материал, обладающий этим свойством, называется хрупким. К хрупким материалам относятся чугун, высокоуглеродистая сталь, стекло, кирпич, бетон, природные камни. Характерная диаграмма деформации хрупких материалов изображена на рис. 2.11.
Диаграмма растяжения
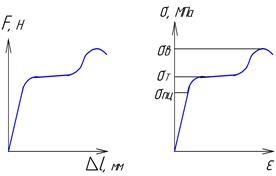 Прежде чем исходные данные по напряжениям поступят в справочную литературу, их надо получить. Получают их, проводя серии испытаний на образцах из данного материала. Первый вид испытаний – это испытание на разрыв. Образец закрепляется в разрывной машине и растягивается до полного разрушения. При этом фиксируются сила и деформация образца. Большинство материалов, с которыми нам приходится сталкиваться (стали, алюминиевые и медные сплавы и др.) относятся к группе упруго-пластичных материалов. Их диаграмма растяжения выглядит, как показано на рис.1.4а. Сначала деформация растет пропорционально силе, затем резкое увеличение деформации (текучесть материала), снова сопротивление и разрыв
Прежде чем исходные данные по напряжениям поступят в справочную литературу, их надо получить. Получают их, проводя серии испытаний на образцах из данного материала. Первый вид испытаний – это испытание на разрыв. Образец закрепляется в разрывной машине и растягивается до полного разрушения. При этом фиксируются сила и деформация образца. Большинство материалов, с которыми нам приходится сталкиваться (стали, алюминиевые и медные сплавы и др.) относятся к группе упруго-пластичных материалов. Их диаграмма растяжения выглядит, как показано на рис.1.4а. Сначала деформация растет пропорционально силе, затем резкое увеличение деформации (текучесть материала), снова сопротивление и разрыв
|
|
образца.
а) Рис.1 б)
В виде а) информация потребителю не нужна, поэтому диаграмма перестраивается в координатах σ и ε – относительная деформация.
На диаграмме выделяются 3 характерных точки σпц – предел пропорциональности, σТ – предел текучести и
σв - временное сопротивление или предел прочности.
После обработки результатов испытаний в справочную литературу передаются данные, имеющие наименьшую погрешность – это в первую очередь σв, затем σТ, а σпц вы можете встретить крайне редко, только в специальной литературе.
А теперь внимательно посмотрите на диаграмму и ответьте на вопрос, какие напряжения Вы можете брать в качестве допустимых? σв – очевидно нет, поскольку Вы заведомо закладываете в конструкцию ее разрушение; σТ - крайне не желательно, при этих напряжениях в конструкции возникнут значительные, необратимые пластические деформации; σпц – можно, только Вам его никто не дал. Получается замкнутый круг, что дано – брать нельзя, а что можно брать – то не дано. Выход из этого круга Вам предлагают искать самим.
[σ] = σв/n, (1.1)
где n = 1,2 … 10 – коэффициент запаса прочности.
 В каждом конкретном случае Вам самим придется решать, какой коэффициент запаса прочности выбрать. Возьмете маленький коэффициент – конструкция будет легкой, но может разрушиться. Возьмете большой коэффициент – конструкция может оказаться слишком громоздкой и тяжелой. Поиск компромиса – довольно серьезная проблема. Очень многое будет зависеть от условий, в которых будет работать Ваше изделие с точки зрения опасности. Например, Вам нужно спроектировать две однотипных тележки, только одна предназначена для дачи, а на другой будут перевозить бутыли с сверхядовитым веществом и поломка этой тележки чревата катастрофическими последствиями. Одинаковый ли коэффициент запаса прочности Вы возьмете в этих случаях?
В каждом конкретном случае Вам самим придется решать, какой коэффициент запаса прочности выбрать. Возьмете маленький коэффициент – конструкция будет легкой, но может разрушиться. Возьмете большой коэффициент – конструкция может оказаться слишком громоздкой и тяжелой. Поиск компромиса – довольно серьезная проблема. Очень многое будет зависеть от условий, в которых будет работать Ваше изделие с точки зрения опасности. Например, Вам нужно спроектировать две однотипных тележки, только одна предназначена для дачи, а на другой будут перевозить бутыли с сверхядовитым веществом и поломка этой тележки чревата катастрофическими последствиями. Одинаковый ли коэффициент запаса прочности Вы возьмете в этих случаях?
Коэффициент запаса прочности – это Ваш опыт, страх и риск.
Могу Вам дать только небольшой совет.
Условия работы конструкции:
неопасные n = 1,2 … 2,5;
средней опасности n = 2,5 … 5;
повышенной и высокой опасности n = 5 … 10 и более.
На данный момент Вы уже многое знаете. Знаете, что такое напряжение, какие виды напряжений бывают, можете определить внутренние силы, можете решить вопрос с допустимыми напряжениями. Вы готовы к решению прочностных задач. Поэтому перейдем к рассмотрению конкретных видов деформаций.
13. Внутренние силовые факторы, поперечная сила и изгибающий момент
Под влиянием внешей нагрузки реальные тела деформируются, в отличие от абсолютно твердого тела, изучаемого в курсе теоретической механики. При этом между рядом раположенными частицами тела воникают, по законам физики, внутренние силы. Если мысленно рассечь деформированный брус плоским перечным сечением на две части и привести внутренние силы, действующие со стороны одной части на другую - к центру тяжести (площади) поперечного сечения, получим ГЛАВНЫЙ ВЕКТОР R и ГЛАВНЫЙ МОМЕНТ M системы этих внутренних сил. Эти величины (R и M) имеют такой смысл:
Если мысленно заменить внутренние силы, действующие в сечении, силой R и моментом (парой сил) M (приложив их в центре тяжести поперечного сечения), то равновесие отсеченной части тела не нарушится. То есть R и M (совместно) являются статическим эквивалентом системы внутренних сил, действующих в сечении.
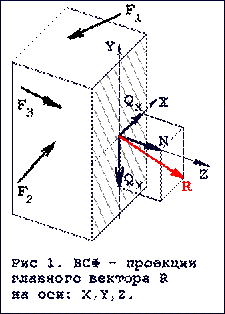
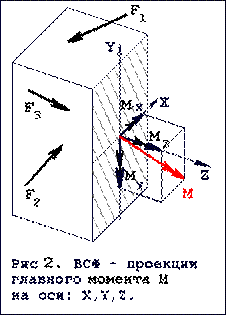

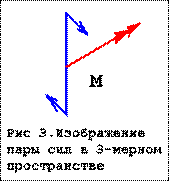
Рис. 1,2,3: Внутренние силовые факторы (ВСФ) в поперечном сечении бруса
Проекции главного вектора R и главного момента M на ГЛАВНЫЕ ЦЕНТРАЛЬНЫЕ ОСИ поперечного сечения и ПРОДОЛЬНУЮ ось бруса называются ВНУТРЕННИМИ СИЛОВЫМИ ФАКТОРАМИ (ВСФ) в поперечном сечении. ВСФ (см рис 1) обозначаются:
· Проекция R на ось Z т е N называется продольной силой.
· Проекция R на ось Y т е QY называется поперечной силой.
· Проекция R на ось X т е QX тоже называется поперечной силой.
· Проекция M на ось Z т е MZ называется крутящим моментом.
· Проекция M на ось Y т е MY называется изгибающим моментом (в горизонтальной плоскости XZ).
· Проекция M на ось X т е MX тоже называется изгибающим моментом (в вертикальной плоскости YZ). Примечание:
Существует два способа изображения пары сил:
1. В виде вектора - как показано на рис. 2
2. В виде пары сил.
Чтобы перейти от одного способа к другому применяется ПРАВИЛО БУРАВЧИКА (см рис 3)
(Пример вычисления величины ВСФ и построения эпюр см здесь)