В качестве иллюстрации понятия "внутренние силовые факторы" рассмотрим пример - балку, к которой приложена нагрузка, действующая в вертикальной плоскости (плоскость YZ - см рис 1,2, 4.1). Так как продольная ось Z балки и внешняя нагрузка q находятся в одной плоскости (YZ) и реакции опор A и B - YA, YB - в этой же плоскости, то задача является плоской и можно изобразить расчетную схему в плоскости рисунка (см рис 4.2, 4.3, 4.4).
Выделим двумя бесконечно близкими друг к другу (расстояние dz) поперечными сечениямим тонкий элемент балки (см 4.1, 4.2, 4.3, 4.4) и рассмотрим его равновесие под действием ВСЕХ приложенных к нему внешних сил.
· Имеется в виду, что мы мысленно вырезали элемент из балки, заменив действие внутренних сил, действовавших со стороны левой и правой отброшенных частей статическими эквивалентами - внутренними силовыми факторами (Q,M - слева, Q+dQ, M+dM - справа.)
· Поэтому равновесие этого элемента (если оно было) - не нарушится. Но было ли равновесие? Конечно, потому что в сопротивлении материалов рассматриваются, как правило, неподвижные (покоящиеся) конструкции и их элементы. Из курса теоретической механики известно, что если тело находится в состоянии покоя (или равномерного прямолинейного движения относительно инерциальной системы координат) то система внешних сил, приложенных к этому телу, взаимно уравновешена.
· Обратите внимание, что ВСФ, приложенные к левой и правой границам отсекаемого элемента ВЗАИМНО ПРОТИВОПОЛОЖНЫпо направлению. Поэтому никак не возможно для ВСФ - поперечной силы Q и изгибающего момента M принять правила знаков + -, установленные в статике для сосредоточенных сил и пар сил. Правила знаков для ВСФ рассмотрим позже. Естественно, что в общем случае мы допускаем возможность изменения Q и M, поэтому к правой границе элемента прикладываем ВСФ: Q+dQ и M+dM. Остальные ВСФ (если они есть) не рассматриваем, так как они не входят в уравнения равновесия, которые будут рассмотрены.
· Рассмотрим уравнения равновесия отсеченного элемента с целью получить зависимости между q, Q и M (см рис 4.4).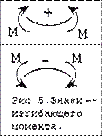 
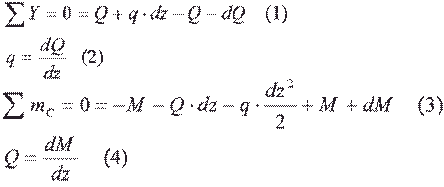
Формула (2) получена из ф. (1), а формула (4) - из ф. (3) - с учетом того, что dz2 - бесконечно малая величина более высокого порядка, чем dz и может быть удалена.
Знаки ВСФ
В сопротивлении материалов принято следующее ПРАВИЛО ЗНАКОВ для ВСФ.:
· Продольная сила N считается положительной, если она направлена в сторону ВНЕШНЕЙ нормали к сечению, то есть РАСТЯГИВАЕТ элемент, показанный на рис 4.4 и отрицательной, если она СЖИМАЕТ элемент.
· Поперечная сила QY (при расчете балок и плоских рам она обычно обозначается просто Q) считается положительной, если она направлена в сторону внешней нормали к сечению, ПОВЕРНУТОЙ на 90o ПО ЧАСОВОЙ СТРЕЛКЕ.
· Изгибающий момент MX считается положительным (для БАЛОК и горизонтальных участков РАМ), если он деформирует продольную ось бруса выпуклостью вниз (т е сжатые продольные "волокна" расположены сверху, а растянутые - снизу - см рис 5). В противном случае (выпуклостью вверх, сжатые волокна внизу, растянутые - вверху) изгибающий момент считается отрицательным. Здесь: ось X перпендикулярна плоскости рисунка 4.4 и проходит через точку С - центр тяжести (площади) поперечного сечения. При расчете балок и плоских рам MX обычно обозначается просто M.
· Все ВСФ, показанные на рис. 4.4 ПОЛОЖИТЕЛЬНЫ. И в дальнейшем - неизвестные ВСФ будем предполагать ПОЛОЖИТЕЛЬНЫМИ. Тогда полученные в результате решения значения (включая знак) легко понять.
Эпюры ВСФ
График зависимости величины какого-либо ВСФ от координаты z поперечного сечения, в котором действует этот ВСФ называется ЭПЮРОЙ. Эпюры имеют большое значение в расчетах на прочность, так как позволяют легко определить сечение, в котором брус максимально нагружен (если поперечное сечение одинаково по всей длине бруса). Такое сечение называется ОПАСНЫМ сечением.
ИЗГИБ
ИЗГИБ – один из основных видов деформации балки, когда прямолинейная балка под действием внешних нагрузок приобретает криволинейную форму. (Корни слова «балка» – немецкие и первоначально это слово означало «бревно»). Во многих конструкциях балка является основным элементом; примером являются многие типы перекрытий, мостов и т.д.
Балка как конструктивный элемент обычно или закреплена концами на соответствующих опорах, или одним концом заделана в стену, тогда как другой конец оказывается свободным (в этом случае балку называют «консоль»), рис.1 (а, б).
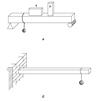
В некоторых местах балка взаимодействуют с другими телами; схематизируя ситуацию (рис. 2), говорят, что в известных точках к балке приложены заданные сосредоточенные силы P, Q или распределенные нагрузки интенсивности q (килоньютонов на метр).
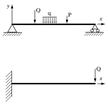
Примером распределенных нагрузок является собственный вес балки или вес достаточно длинного постороннего тела, лежащего на балке (например, снега). Нагрузки (или их часть), направленные перпендикулярно к балке, вызывают ее изгиб; направленные вдоль балки вызывают растяжение или сжатие. Задачей теории изгиба балок является определение прогиба балки под нагрузками, а также напряжений и деформаций в материале балки, естественно, что форма, размеры, материал балки и внешние нагрузки считаются заданными. Затем, при расчете на прочность, задачу трансформируют так: каковы должны быть размеры сечения балки, чтобы при заданных нагрузках напряжения не превышали бы допустимых значений?
Теория изгиба балки была создана Я.Бернулли и Л.Эйлером на рубеже 17–18 вв. Для простоты балка заменяется отрезком прямой, причем считается, что упругие свойства этого отрезка такие же, как у исходной балки. После приложения нагрузок отрезок изгибается и становится криволинейным. Получившаяся кривая называется упругой линией или эластикой. Задача – найти ее уравнение у = f (x). Решение этой задачи основано на утверждении, что в каждой точке упругой линии ее кривизна пропорциональна изгибающему моменту внешних сил, который зависит от координаты x и обозначается M (x). Так как при малых прогибах, которые в первую очередь интересуют инженеров, кривизна кривой практически равна ее второй производной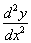 
, можно записать дифференциальное уравнение:
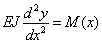
Коэффициент пропорциональности EJ называется изгибной жесткостью, он определяет способность балки сопротивляться изгибу и равен произведению модуля упругости материала балки E на момент инерции сечения балки J, который для прямоугольного бруса выражается формулой
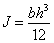
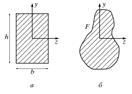
где b – ширина сечения, а h – высота (рис. 3,а).
Если сечение балки есть фигура F (рис. 3,б), и начало координат проходит через центр масс сечения, то
J = òò y\up122 dF
т.е. момент инерции площади F определяется как двойной интеграл по этой площади. Название «момент инерции» связано с тем, что этот интеграл в динамике твердого тела связан с инерционными характеристиками тела.
Изгибная жесткость учитывает и упругость материала, и форму и размеры сечения балки.
Изгибающий момент M (x) полностью определяется величиной и положением нагрузок и находится по правилам статики. Например, если в консольной балке, нагружаемой на конце силой P, (рис. 2), мысленно провести сечение через точку с координатой x, то момент силы P относительно точки x выражается очевидной формулой
M = Px
(система координат показана на рис. 4), при изменении расстояния сечения от конца балки момент M растет линейно; этот график называют эпюрой изгибающего момента M (x). Напряжения s в сечениях балки пропорциональны M (x):
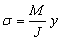
(координата y отсчитывается вверх от центра сечения).
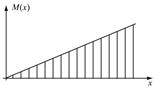
В качестве примера можно рассмотреть две одинаковые балки: одну – на двух шарнирных опорах, другую – консольную, нагруженные одинаковыми силами P в середине пролета и на конце соответственно. Длина балок l, сечение – прямоугольник b × h. Прогиб первой балки в середине пролета равен
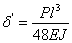
Прогиб на конце второй балки равен
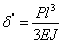
Для сравнения укажем, что если ту же балку растягивать силой P, то ее удлинение будет равно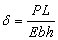 
. Напряжения и деформации в изогнутой балке распределены таким образом, что внешние волокна растянуты, а внутренние – сжаты, причем и напряжения s, и деформации e растут пропорционально расстоянию от середины сечения балки, точнее – от нейтральной линии, где s = 0, и e = 0. Другими словами, внешние слои балки несут большую часть нагрузки, внутренние – значительно меньшую. Поэтому целесообразно так организовать форму сечения балки, чтобы большая часть материала была удалена от центра сечения. Двутавровые (т.е. в виде двойного «Т») и трубчатые сечения балок являются типичными примерами оптимальных (т.е. наилучших в некотором смысле) сечений.
Назначение передач
Все современные двигатели для уменьшения габаритов и стоимости выполняют быстроходными с весьма узким диапазоном изменения угловых скоростей. Непосредственно быстроходный вал двигателя соединяют с валом машины редко (вентиляторы и т. п.).
В абсолютном большинстве случаев режим работы рабочей машины не совпадает с режимом работы двигателя, поэтому передача механической энергии от двигателя к рабочему органу машины осуществляется с помощью различных передач.
- требуемые скорости рабочих органов машины часто не совпадают со скоростями стандартных двигателей;
- скорости рабочего органа машины часто необходимо регулировать (изменять) в процессе работы;
- большинство рабочих органов машин должны работать при малых скоростях и обеспечивать большие вращающие моменты, а высокооборотные двигатели экономичнее;
- двигатели изготовляют для равномерного вращательного движения, а в машинах иногда требуется прерывистое поступательное движение с изменяющимися скоростями.