Рассмотрим последовательность -1,3,7,11. Требуется предсказать следующие два числа и найти закономерность последовательности. Первый вариант: 15,19. Закономерность Ha есть последующее число есть предыдущее плюс 4, иначе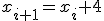 
. Второй вариант-19,9,1043,8. Закономерность Hc
есть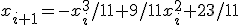 
.
С одной стороны, возможно непосредственно назначить априорные вероятности для обеих моделей так, чтобы штрафовать более сложную модель. С другой стороны, возможно вычислить их правдоподобие, P(D/Ha) и P(D/Hc) чтобы определить, насколько хорошо обе функции описывают данные.
Модель Ha зависит от двух параметров: добавляемого числа n и от первого числа в последовательности. Пусть каждый из этих параметров принадлежит множеству (-50,…,50)∈Z. Так как только пара значений (n=4,x1=
=-1) доставляют функцию, соответствующую данным D=(-1,3,7,11), то вероятность появления данных D при заданной модели Ha равна
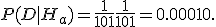
Для того, чтобы вычислить P(D/Hc), требуется вычислить вероятность параметров c,d,e в кубическом многочлене Hc.
Эти параметры представлены с виде рациональных чисел (в противном случае обе эти модели были бы несравнимы). Пусть числители параметров, так же как и в предыдущем случае, принимают значения из множества (-50,…,50) а знаменатели — из множества(1,…,50)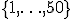 
. При вычислении вероятности принимается во внимание, что несколько способов представить дробь на заданных множествах. Например, 
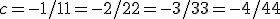. Вероятность 
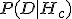равна
Отношение правдоподобия двух моделей (а значит и их апостериорных вероятностей при условии равенства априорных предпочтени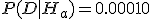й), 
и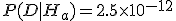 
составляет одну сорокамиллионную.[1]
Глава 2. Байесовские сети доверия как средство разработки ЭС
Байесовские сети доверия используются в тех областях, которые характеризуются наследованной неопределённостью. Эта неопределённость может возникать вследствие: неполного понимания предметной области; неполных знаний; когда задача характеризуется случайностью.
|
|
Таким образом, байесовские сети доверия (БСД) применяют для моделирования ситуаций, содержащих неопределённость в некотором смысле. Для байесовских сетей доверия иногда используется ещё одно название причинно-следственная сеть, в которых случайные события соединены причинно-следственными связями.
Соединения методом причин и следствий позволяют более просто оценивать вероятности событий. В реальном мире оценивание наиболее часто делается в направлении от "наблюдателя" к "наблюдению", или от "эффекта" к "следствию", которое в общем случае более сложно оценить, чем направление "следствие -> эффект", то есть в направлении от следствия.
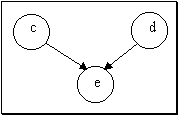
Рис.2. Пример простейшей байесовской сети доверия.
Рассмотрим пример сети (рис.2), в которой вероятность пребывания вершины "e" в различных состояниях (ek) зависит от состояний (ci, dj) вершин "c" и "d" и, в общем случае, определяется выражением:
где p (ek | ci, dj) - условная вероятность пребывания вершины "e" в состоянии (ek) в зависимости от состояний (ci, dj), в которых находятся вершины "с" и "d". Но так как события, представленные вершинами "c" и "d" являются независимыми, то есть между ними отсутствует причинно-следственная связь, то их совместная вероятность может быть представлена в виде:
p (ci, dj) = p (ci) * p (dj)
Рассмотрим пример более сложной сети (рис.3). Данный рисунок иллюстрирует условную независимость событий "с" и "d" от воздействующих на них групп событий.
|
|
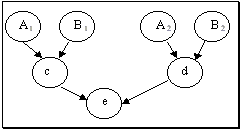
Рис.3. Двухуровневая БСД.
Для оценки вероятности пребывания вершины "e" в различных состояниях следует использовать приведенное выше выражение. Что же касается вершин "c" и "d", то для их оценки будем использовать выражения, аналогичные тому, что и для вычисления p (ek), тогда:
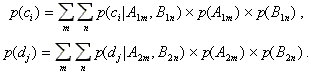
Из этих выражений видно, что вершина "e" условно не зависит от вершин А1,А2,В1,В2, так как нет стрелок непосредственно соединяющих эти вершины.
Рассмотрев эти примеры попробуем теперь более точно определить основные понятия, используемые в БСД. Байесовские сети доверия - это направленный ациклический граф, обладающий следующими свойствами:
· каждая вершина представляет собой событие, описываемое случайной величиной, которая может иметь несколько состояний;
· все вершины, связанные с "родительскими" определяются таблицей условных вероятностей (ТУВ) или функцией условных вероятностей (ФУВ);
· для вершин без "родителей" вероятности её состояний являются безусловными (маргинальными).
Другими словами, в байесовских сетях доверия вершины представляют собой случайные переменные, а дуги - вероятностные зависимости, которые определяются через таблицы условных вероятностей. Таблица условных вероятностей каждой вершины содержит вероятности состояний этой вершины при условии состояний её "родителей".
Далее ознакомимся с примером построения простейшей байесовской сети доверия. В этом примере рассматриваем небольшую яблочную плантацию "яблочного Джека". Однажды Джек обнаружил, что его прекрасное яблочное дерево лишилось листвы. Теперь он хочет выяснить, почему это случилось. Он знает, что листва часто опадает, если:
|
|
1. дерево засыхает в результате недостатка влаги;
2. дерево болеет.
Данная ситуация может быть смоделирована байесовской сетью доверия, содержащей 3 вершины: "Болеет", "Засохло" и "Облетело".
Рис.4. Пример байесовской сети доверия с тремя событиями.
В данном простейшем случае рассмотрим ситуацию, при которой каждая вершина может принимать всего лишь два возможных состояний и, как следствие находится в одном из них, а именно:
Таблица1
| Вершина (событие) БСД | Состояние 1 | Состояние 2 |
| "Болеет" | "болеет" | "нет" |
| "Засохло" | "засохло" | "нет" |
| "Облетело" | "да" | "нет" |
вершина "Болеет" говорит о том, что дерево заболело, если оно находится в состоянии "болеет", в противном случае она находится в состоянии "нет". Аналогично для других двух вершин. Рассматриваемая байесовская сеть доверия, моделирует тот факт, что имеется причинно-следственная зависимость от события "Болеет" к событию "Облетело" и от события "Засохло" к событию "Облетело". Это отображено стрелками на байесовской сети доверия.
Когда есть причинно-следственная зависимость от вершины А к другой вершине B, то мы ожидаем, что когда A находится в некотором определённом состоянии, это оказывает влияние на состояние B. Следует быть внимательным, когда моделируется зависимость в байесовских сетях доверия. Иногда совсем не очевидно, какое направление должна иметь стрелка.
Например, в рассматриваемом примере, мы говорим, что имеется зависимость от "Болеет" к "Облетело", так как когда дерево болеет, это может вызывать опадание его листвы. Опадание листвы является следствием болезни, а не болезнь - следствием опадания листвы.
На приведенном выше рисунке дано графическое представление байесовской сети доверия. Однако, это только качественное представление байесовской сети доверия. Перед тем, как назвать это полностью байесовской сетью доверия необходимо определить количественное представление, то есть множество таблиц условных вероятностей:
Таблица 2
Приведенные таблицы иллюстрируют ТУВ для трёх вершин байесовской сети доверия. Заметим, что все три таблицы показывают вероятность пребывания некоторой вершины в определённом состоянии, обусловленным состоянием её родительских вершин. Но так как вершины Болеет и Засохло не имеют родительских вершин, то их вероятности являются маргинальными, т.е. не зависят (не обусловлены) ни от чего.
На данном примере мы рассмотрели, что и как описывается очень простой байесовской сетью доверия. Современные программные средства (такие как MSBN, Hugin и др.) обеспечивают инструментарий для построения таких сетей, а также возможность использования байесовских сетей доверия для введения новых свидетельств и получения решения (вывода) за счёт пересчёта новых вероятностей во всех вершинах, соответствующих вновь введенным свидетельствам.
В нашем примере пусть известно, что дерево сбросило листву. Это свидетельство вводится выбором состояния "да" в вершине "Облетело". После этого можно узнать вероятности того, что дерево засохло. Для приведенных выше исходных данных, результаты вывода путем распространения вероятностей по БСД будут:
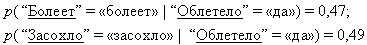
Кроме того, следует отметить, что следствием байесовской теоремы является то, что она поддерживает оценку графа в обоих направлениях. Процесс рассуждения в ЭС сопровождается распространением по сети вновь поступивших свидетельств.
Введение в байесовские сети доверия новых данных приводит к возникновению переходного процесса распространения по байесовской сети доверия вновь поступившего свидетельства. После завершения переходного процесса каждому высказыванию, ассоциированному с вершинами графа, приписывается апостериорная вероятность, которая определяет степень доверия к этому высказыванию:
где
D - объединения всех поступивших в систему данных;
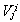- композиционные высказывания, составленные из элементарных, то есть множество значений 
составляют ;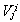
- пропозиционные переменные (то есть переменные, значениями которых являются высказывания), определяющие состояние вершин БСД.
При этом процесс распространения вероятностей в БСД основывается на механизме пересчёта, в основе функционирования которого лежит следующая последовательность действий:
1. С каждой вершиной сети ассоциирован вычислительный процесс (процессор), который получает сообщения от соседних (связанных с ним дугами) процессоров.
2. Этот процессор осуществляет пересчёт апостериорных вероятностей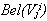 
для всех возможных значений 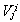данной переменной и посылает соседим вершинам ответные сообщения.
3. Деятельность процессора инициируется нарушением условий согласованности с состояниями соседних процессоров и продолжается до восстановления этих условий.
В некоторых системах, реализующих байесовские сети доверия используется метод noisy or gate, позволяющий существенно упростить вычислительный процесс. Суть его заключается в том, что в ряде примеров вершина "y" может быть условно независима от целого ряда вершин "xi", где i = 1,2,..., n. Для того, чтобы сократить оценку 2n вероятностей, которые необходимы при использовании таблиц условных вероятностей, и используется данный метод. Согласно ему вероятность "y" в зависимости от n вершин "xi" оценивается как
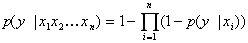
что позволяет оценить только p(y | x1), p(y | x2),..., p(y | xn), и на их основании определить оценку p(y | x1 x2... xn).
Байесовские сети доверия являются одним из направлений современных экспертных систем
Выбор байесовских сетей доверия в качестве ЭС по сравнению с другими направлениями их построения обусловлен рядом причин.
Логический вывод в байесовских сетях доверия является трактуемым с вычислительной точки зрения, так как теория, лежащая в его основе, имеет аксиоматическое обоснование, отработанное в течение последних десятилетий. В то время, как системы, основанные на теории нечётких множеств, на теории функций доверия, теории Демпстера - Шефера не имеет строгого математического обоснования и в большинстве случаев используют эвристические процедуры (ЭС типа MYCIN, EMYCIN и т.д.).
Показано, что психологически проще выполнять субъективное вероятностное оценивание причинно-следственных связей.
Метод noisy or gate обеспечивает эффективное вычисление условных вероятностей.
Несмотря на то, что теорию вероятности зачастую критикуют с точки зрения её использования в "знаниях", она не нарушает общих представлений о "замкнутом мире" объектов.
Одними из наиболее распространённых для современных ПЭВМ программных систем, реализующих теорию байесовских сетей доверия, являются: "MSBN" фирмы Microsoft и "Hugin" фирмы Hugin AIS, Дания
Hugin является программой реализацией системы принятия решений на основе байесовских сетей доверия. Имеет две версии Pro и Explorer. Функционирует в среде OS Windows, а также имеет версию под UNIX. Эта система имеет развитый интерфейс и позволяет достаточно просто создавать базы знаний и фактов. Использует два основных режима работы:
режим редактирования и построения причинно-следственной сети, а также заполнения таблиц условных вероятностей, являющихся количественным описанием БЗ.
Режим расчёта вероятностных оценок для принятия решения по всем событиям, входящим в причинно-следственную сеть.
Расчёты могут осуществляться как на основе классической теории Байеса, так и на основе методов теории возможностей. "Hugin" имеет возможность связи с основными наиболее распространёнными программными средствами фирмы Microsoft. Данная ЭС имеет все основные функции любой информационной системы, включая такие как: хранение данных, вывод на принтер всех элементов ЭС, диагностика ошибок в работе.[2]
Заключение
В данной статье мы рассмотрели байесовский анализ и его применение. Использование методологии Байеса в формировании статистических выводов дает возможность совсем по-иному воспринимать и исследовать оцениваемые модели. Он позволяет оперировать не только полученными оценками, а также соответствующими вероятностными распределениями, применять имеющиеся в разных формах априорные знания исследователя относительно оценок параметров модели. Это дает возможность получать большие объемы исходной информации и точнее описывать структуру и другие характеристики исследуемой модели.
Список используемой литературы
1.. Гмурман В. Е. Теория вероятностей и математическая статистика, — М.: Высшее образование. 2005
2.Пример применения подхода. Байесовский подход к принятию решений и его применение в условиях страхования, гарантийного обслуживания и принятия решения с проведением экспериментов. https://www.levvu.narod.ru
3. Орлов А. И. Теория принятия решений: учебник. – М.: Экзамен, 2006.
4.Лопатников Л. И. Экономико-математический словарь: Словарь современной экономической науки. — 5-у изд., перераб. и доп. — М.: Дело, 2003. — 520 с.
5.Моделирование процессов принятия решений в производственно-экономической системе / Макаров К. Г., Очкас М. В., Петренко В. Л., Ремпель А. Г.; Донец. гос. ун-т. — Донецк: ДонГУ, 1998. — 27 с. Недосекин А. О.
6.Применение теории нечетких множеств к задачам управления финансами [Электронный ресурс] / А. О. Недосекин // Аудит и финансовый анализ. — 2000. — № 2. — Режим доступа: https://www. cfin.ru/press /afa/2000–2/08.shtml
7.Фомин В. Н., Фрадков А. Л., Якубович В. А. Адаптивное управление динамическими объектами. — М.: Наука, 1981. — 184 с. Шапиро Л. Д. и др.
Интернет ресурсы
8. www. cfin.ru/press /afa/2000
9.https://habr.com/post/170545
10. https://www.machinelearning.ru/wiki/images/4/43/BayesML-2007-textbook-2.pdf
[1] https://www.machinelearning.ru/wiki/images/4/43/BayesML-2007-textbook-2.pdf
[2] Адаптивное управление динамическими объектами. — М.: Наука, 1981. — 184 с.