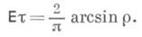Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.
Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:
1) Сопоставать каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию).
2) Определить разности рангов каждой пары сопоставляемых значений.
3) Возвести в квадрат каждую разность и суммировать полученные результаты.
4) Вычислить коэффициент корреляции рангов по формуле:.
где 
- сумма квадратов разностей рангов, а 
- число парных наблюдений.
При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента равные 0,3 и менее, показателями слабой тесноты связи; значения более 0,4, но менее 0,7 - показателями умеренной тесноты связи, а значения 0,7 и более - показателями высокой тесноты связи.
Мощность коэффициента ранговой корреляции Спирмена несколько уступает мощности параметрического коэффициента корреляции.
Коэффицент ранговой корреляции целесообразно применять при наличии небольшого количества наблюдений. Данный метод может быть использован не только для количественно выраженных данных (пример 1), но также и в случаях, когда регистрируемые значения определяются описательными признаками различной интенсивности (пример 2).
КЕНДАЛЛА КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕЛЯЦИИ
- одна из выборочных мер зависимости двух случайных величин (признаков) Xи Y, основанная на ранжировании элементов выборки (X1, Yx) ,..., (Х п, Yn). К. к. р. к. относится, таким образом, к ранговым статистикам и определяется формулой
где ri - ранг У, принадлежащего той паре (X, Y), для к-рой ранг Xравен i, S = 2N -(п-1)/2, N-число элементов выборки, для к-рых одновременно j>i и rj>ri. Всегда 
В качестве выборочной меры зависимости К. к. р. к. широко использовался М. Кендаллом (М. Kendall, см. [1]).
К. к. р. к. применяется для проверки гипотезы независимости случайных величин. Если гипотеза независимости верна, то Et=0 и Dt=2(2n+5)/9n(n-1). При небольшом объеме выборки 
проверка статистич. гипотезы независимости производится с помощью специальных таблиц (см. [3]). При n>10 пользуются нормальным приближением для распределения т: если
то гипотеза о независимости отвергается, в противном случае принимается. Здесь a. - уровень значимости, ua/2 есть 
процентная точка нормального распределения. К. к. р. к., как и любая ранговая статистика, может использоваться для обнаружения зависимости двух качественных признаков, если только элементы выборки можно упорядочить относительно этих признаков. Если X, Y имеют совместное нормальное распределение с коэффициентом корреляции р, то связь между К. к. р. к. и имеет вид:
