Квадратическая взвешенная

Средняя квадратическая взвешенная равна:

Средняя геометрическая применяется при определении средних относительных изменений, о чем сказано в теме Ряды динамики. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.

Среднегеометрическая величина дает возможность сохранять в неизменном виде не сумму, а произведение индивидуальных значений данной величины. Ее можно определить по следующей формуле:

Среднегеометрические величины наиболее часто используются при анализе темпов роста экономических показателей.

Геометрическая простая

Для расчетов средней геометрической простой используется формула:

где:

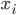• — цепной коэффициент роста
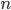• — число этих коэффициентов роста
• П — знак произведения
• — количество уровней ряда
• — значение начального уровня ряда
• — значение конечного уровня ряда

Геометрическая взвешенная

Для определения средней геометрической взвешенной применяется формула:

Как определяются размах вариации, среднее линейное отклонение?

Стр. 23-25 в методичке

Размах вариации. Все признаки, отмеченные в статистике, подвержены колебанию. Самым простым показателем такой колеблимости любого признака является размах вариации. В общем случае он представляет собой разность между наибольшим и наименьшим значением признака. Размах вариации зависит от двух значений признака, что в экономике означает неточность определения. Среднее линейное отклонение. Измерителем среднего линейного отклонения считается величина отклонений от средней, взятых без учета алгебраического знака. Исчисленная таким образом величина среднего отклонения называется средним линейным отклонением. В практике следует иметь в виду, что величины линейного отклонения различных вариационных рядов можно сравнить лишь в том случае, если эти ряды характеризуются примерно одинаковыми средними. А т.к. это бывает в практике не всегда, то для сопоставления колеблимости исчисляются относительные показатели колеблимости, т.е. относят линейные отклонения к арифметической средней. Используя ранее принятые обозначения варьирующего признака, веса и средней, можно порядок расчета среднего линейного отклонения записать в виде формулы . Но в случае, если варианты в распределении признака не повторяются, то среднее линейное отклонение рассчитывается по следующей формуле:

Какие существуют методы расчета дисперсия, среднего квадратического отклонения, коэффициент вариации?

Стр. 25-30, Коэффициент вариации используют для сравнения рассеивания двух и более признаков, имеющих различные единицы измерения. Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах. Он вычисляется по формуле:

,ь

где - искомый показател, - среднее квадратичное отклонение, - средняя величина.