Однофакторный дисперсионный анализ: примеры

Дисперсионный анализ: соединение теории и практики

· Дисперсионный анализ: основные понятия

· Однофакторный дисперсионный анализ: суть метода, формулы, примеры

· Однофакторный дисперсионный анализ в MS Excel

· Двухфакторный дисперсионный анализ без повторений: суть метода, формулы, пример

· Двухфакторный дисперсионный анализ без повторений в MS Excel

· Двухфакторный дисперсионный анализ с повторениями: суть метода, формулы, пример

· Двухфакторный дисперсионный анализ с повторениями в MS Excel

Дисперсионный анализ: основные понятия

Для чего применяется дисперсионный анализ? Цель дисперсионного анализа - исследование наличия или отсутствия существенного влияния какого-либо качественного или количественного фактора на изменения исследуемого результативного признака. Для этого фактор, предположительно имеющий или не имеющий существенного влияния, разделяют на классы градации (говоря иначе, группы) и выясняют, одинаково ли влияние фактора путём исследования значимости между средними в наборах данных, соответствующих градациям фактора. Примеры: исследуется зависимость прибыли предприятия от типа используемого сырья (тогда классы градации - типы сырья), зависимость себестоимости выпуска единицы продукции от величины подразделения предприятия (тогда классы градации - характеристики величины подразделения: большой, средний, малый).

Минимальное число классов градации (групп) - два. Классы градации могут быть качественными либо количественными.

Почему дисперсионный анализ называется дисперсионным? При дисперсионном анализе исследуется отношение двух дисперсий. Дисперсия, как мы знаем - характеристика рассеивания данных вокруг среднего значения. Первая - дисперсия, объяснённая влиянием фактора, которая характеризует рассеивание значений между градациями фактора (группами) вокруг средней всех данных. Вторая - необъяснённая дисперсия, которая характеризует рассеивание данных внутри градаций (групп) вокруг средних значений самих групп. Первую дисперсию можно назвать межгрупповой, а вторую - внутригрупповой. Отношение этих дисперсий называется фактическим отношением Фишера и сравнивается с критическим значением отношения Фишера. Если фактическое отношение Фишера больше критического, то средние классов градации отличаются друг от друга и исследуемый фактор существенно влияет на изменение данных. Если меньше, то средние классов градации не отличаются друг от друга и фактор не имеет существенного влияния.

Как формулируются, принимаются и отвергаются гипотезы при дисперсионном анализе? При дисперсионном анализе определяют удельный вес суммарного воздействия одного или нескольких факторов. Существенность влияния фактора определяется путём проверки гипотез:

• H 0: μ 1 = μ 2 =... = μ a, где a - число классов градации - все классы градации имеют одно значение средних,
• H 1: не все μ i равны - не все классы градации имеют одно значение средних.

Если влияние фактора не существенно, то несущественна и разница между классами градации этого фактора и в ходе дисперсионного анализа нулевая гипотеза H 0 не отвергается. Если влияние фактора существенно, то нулевая гипотеза H 0 отвергается: не все классы градации имеют одно и то же среднее значение, то есть среди возможных разниц между классами градации одна или несколько являются существенными.

Ещё некоторые понятия дисперсионного анализа. Статистическим комплексом в дисперсионном анализе называется таблица эмпирических данных. Если во всех классах градаций одинаковое число вариантов, то статистический комплекс называется однородным (гомогенным), если число вариантов разное - разнородным (гетерогенным).

В зависимости от числа оцениваемых факторов различают однофакторный, двухфакторый и многофакторный дисперсионный анализ.

Однофакторный дисперсионный анализ: суть метода, формулы, примеры

Суть метода, формулы

Однофакторный дисперсионный анализ основан на том, что сумму квадратов отклонений статистического комплекса возможно разделить на компоненты:

SS = SS a + SS e,

где

SS - общая сумма квадратов отклонений,

SS a - объяснённая влиянием фактора a сумма квадратов отклонений,

SS e - необъяснённая сумма квадратов отклонений или сумма квадратов отклонений ошибки.

Если через n i обозначить число вариантов в каждом классе градации (группе) и a - общее число градаций фактора (групп), то - общее число наблюдений и можно получить следующие формулы:

общее число квадратов отклонений: ,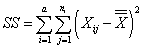

объяснённая влиянием фактора a сумма квадратов отклонений: ,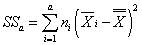

необъяснённая сумма квадратов отклонений или сумма квадратов отклонений ошибки: ,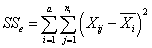

где

- общее среднее наблюдений,

- среднее наблюдений в каждой градации фактора (группе).

Кроме того,

где 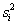- дисперсия градации фактора (группы).

Чтобы провести однофакторный дисперсионный анализ данных статистического комплекса, нужно найти фактическое отношение Фишера - отношение дисперсии, объяснённой влиянием фактора (межрупповой), и необъяснённой дисперсии (внутригрупповой):

и сравнить его с критическим значением Фишера .

Дисперсии рассчитываются следующим образом:

- объяснённая дисперсия,

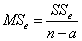- необъяснённая дисперсия,

при этом

v a = a − 1 - число степеней свободы объяснённой дисперсии,

v e = n − a - число степеней свободы необъяснённой дисперсии,

v = n − 1 - общее число степеней свободы.

Критическое значение отношения Фишера с определёнными значениями уровня значимости и степеней свободы можно найти в статистических таблицах или рассчитать с помощью функции MS Excel F.ОБР (рисунок ниже, для его увеличения щёлкнуть по нему левой кнопкой мыши).

Функция требует ввести следующие данные:

Вероятность - уровень значимости α,

Степени_свободы1 - число степеней свободы объяснённой дисперсии v a,

Степени_свободы2 - число степеней свободы необъяснённой дисперсии v e.

Если фактическое значение отношения Фишера больше критического (), то нулевая гипотеза отклоняется с уровнем значимости α. Это означает, что фактор существенно влияет на изменение данных и данные зависимы от фактора с вероятностью P = 1 − α.

Если фактическое значение отношения Фишера меньше критического (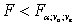), то нулевая гипотеза не может быть отклонена с уровнем значимости α. Это означает, что фактор не оказывает существенного влияния на данные с вероятностью P = 1 − α.

Однофакторный дисперсионный анализ: примеры

Пример 1. Требуется выяснить, влияет ли тип используемого сырья на прибыль предприятия. В шести классах градации (группах) фактора (1-й тип, 2-й тип и т.д.) собраны данные о прибыли от производства 1000 единиц продукции в миллионах рублей в течении 4 лет.

Тип сырья
1-й	7,21	7,55	7,29	7,6
2-й	7,89	8,27	7,39	8,18
3-й	7,25	7,01	7,37	7,53
4-й	7,75	7,41	7,27	7,42
5-й	7,7	8,28	8,55	8,6
6-й	7,56	8,05	8,07	7,84
Среднее	Дисперсия
7,413	0,0367
7,933	0,1571
7,290	0,0480
7,463	0,0414
8,283	0,1706
7,880	0,0563

Число классов градации фактора (групп) a = 6 и в каждом классе (группе) n i = 4наблюдения. Общее число наблюдений n = 24.

Числа степеней свободы:

v a = a − 1 = 6 − 1 = 5,

v e = n − a = 24 − 6 = 18,

v = n − 1 = 24 − 1 = 23.

Вычислим суммы квадратов отклонений:

Вычислим дисперсии:

.

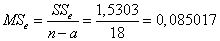Вычислим фактическое отношение Фишера:

.

Критическое значение отношения Фишера:

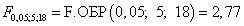
Так как фактическое отношение Фишера больше критического:

,

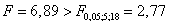с уровнем значимости α = 0,05 делаем вывод, что прибыль предприятия в зависимости от вида сырья, использованного в производстве, существенно отличается.

Или, что то же самое, отвергаем основную гипотезу о равенстве средних во всех классах градации фактора (группах).

В только что рассмотренном примере в каждом классе градации фактора было одинаковое число вариантов. Но, как говорилось во вступительной части, число вариантов может быть и разным. И это ни в коей мере не усложняет процедуру дисперсионного анализа. Таков следующий пример.

Пример 2. Требуется выяснить, существует ли зависимость себестоимости выпуска единицы продукции от величины подразделения предприятия. Фактор (величина подразделения) делится на три класса градации (группы): малые, средние, большие. Обобщены соответствующие этим группам данные о себестоимости выпуска единицы одного и того же вида продукции за некоторый период.

	малый	средний	большой
Среднее	58,6	54,0	51,0
Дисперсия	128,25	65,00	107,60

Число классов градации фактора (групп) a = 3, число наблюдений в классах (группах) n 1 = 4, n 2 = 7, n 3 = 6. Общее число наблюдений n = 17.

Числа степеней свободы:

v a = a − 1 = 2,

v e = n − a = 17 − 3 = 14,

v = n − 1 = 16.

Вычислим суммы квадратов отклонений:

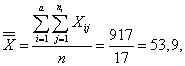
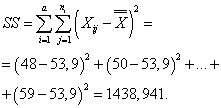
Вычислим дисперсии:

,

.

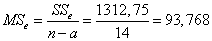Вычислим фактическое отношение Фишера:

.

Критическое значение отношения Фишера:

.

Так как фактическое значение отношения Фишера меньше критического: 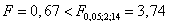, делаем вывод, что размер подразделения предприятия не оказывает существенного влияния на себестоимость выпуска продукции.

Или, что то же самое, с вероятностью 95% принимаем основную гипотезу о том, что средняя себестоимость выпуска единицы одной и той же продукции в малых, средних и крупных подразделениях предприятия существенно не различается.