Пример 3. Дана информация о среднем потреблении топлива на 100 километров в литрах в зависимости от объёма двигателя и вида топлива.
| Бензин со свинцом | |||
| 1001-1500 см³ | 9,3 | ||
| 1501-2000 см³ | 9,4 | ||
| Более 2000 см³ | 12,6 | ||
Среднее 
| 10,42 | ||
| Бензин без свинца | Дизельное топливо | Среднее 
| |
| 8,9 | 6,5 | 8,23 | |
| 9,1 | 7,1 | 8,53 | |
| 9,8 | 8,0 | 10,13 | |
| 9,27 | 7,2 | ||
Требуется проверить, зависит ли потребление топлива от объёма двигателя и вида топлива.
Решение. Для фактора A число классов градации a = 3, для фактора B число классов градации b = 3.
Вычисляем суммы квадратов отклонений:
 ,
,
 ,
,
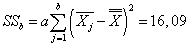 ,
,
 .
.
Соответствующие дисперсии:
 ,
,
 ,
,
 .
.
Фактическое отношение Фишера для фактора A 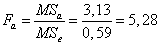 , критическое значение отношения Фишера:
, критическое значение отношения Фишера: 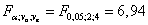 . Так как фактическое отношение Фишера меньше критического, с вероятностью 95% принимаем гипотезу о том, что объём двигателя не влияет на потребление топлива. Однако, если мы выбираем уровень значимости α = 0,1, то фактическое значение отношения Фишера
. Так как фактическое отношение Фишера меньше критического, с вероятностью 95% принимаем гипотезу о том, что объём двигателя не влияет на потребление топлива. Однако, если мы выбираем уровень значимости α = 0,1, то фактическое значение отношения Фишера  и тогда с вероятностью 95% можем принять, что объём двигателя влияет на потребление топлива.
и тогда с вероятностью 95% можем принять, что объём двигателя влияет на потребление топлива.
Фактическое отношение Фишера для фактора B  , критическое значение отношения Фишера:
, критическое значение отношения Фишера:  . Так как фактическое отношение Фишера больше критического значения отношения Фишера, с вероятностью 95% принимаем, что вид топлива влияет на его потребление.
. Так как фактическое отношение Фишера больше критического значения отношения Фишера, с вероятностью 95% принимаем, что вид топлива влияет на его потребление.
Двухфакторный дисперсионный анализ без повторений в MS Excel
Двухфакторный дисперсионный анализ без повторений можно провести с помощью процедуры MS Excel Двухфакторный дисперсионный анализ без повторений. Используем его для анализа данных о связи типа вида топлива и его потребления из примера 3.
В меню MS Excel выполняем команду Сервис/Анализ данных и выбираем средство анализа Двухфакторный дисперсионный анализ без повторений.
Заполняем данные также, как и в случае с однофакторным дисперсионным анализом.

В результате действия процедуры выводятся две таблицы. Первая таблица - Итоги. В ней содержатся данные обо всех классах градации фактора: число наблюдений, суммарное значение, среднее значение и дисперсия.

Во второй таблице - Дисперсионный анализ - содержатся данные об источниках вариации: рассеивании между строками, рассеивании между столбцами, рассеивании ошибки, общем рассеивании, сумма квадратов отклонений (SS), число степеней свободы (df), дисперсия (MS). В последних трёх столбцах - фактическое значение отношения Фишера(F), p-уровень (P-value) и критическое значение отношения Фишера (F crit).
| Дисперсионный анализ | |||||
| Источник вариации | SS | df | |||
| Строки | 6,26 | ||||
| Столбцы | 16,08667 | ||||
| Погрешность | 2,373333 | ||||
| Итого | 24,72 | ||||
| MS | F | P-value | F crit | ||
| 3,13 | 5,275281 | 0,075572 | 6,94476 | ||
| 8,043333 | 13,55618 | 0,016529 | 6,944276 | ||
| 0,593333 | |||||
Фактор A (объём двигателя) сгурппирован в строках. Так как фактическое отношение Фишера 5,28 меньше критического 6,94, с вероятностью 95% принимаем, что потребление топлива не зависит от объёма двигателя.
Фактор B (вид топлива) сгруппирован в столбцах. Фактическое отношение Фишера 13,56 больше критического 6,94, поэтому с вероятностью 95% принимаем, что потребление топлива зависит от его вида.