Алгоритм поиска минимального остовного дерева

Дерево.

Определение. Граф G = (V,E) называется деревом, если он связный и не содержит циклов. В дереве любые две вершины связаны единственной цепью.

Теорема 1. Пусть в дереве G имеется p вершин и q ребер. Тогда q = p-1.

Символом 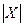будет обозначаться число элементов множества X.

Понятие дерева можно определить различными способами, что вытекает из следующей теоремы.

Теорема 2. Пусть G = (V,E) - неориентированный граф без петель и кратных ребер,

|V| = p, |E| = q. Тогда следующие 5 условий эквивалентны:

1) G - дерево;

2) G - без циклов и q = p-1;

3) G - связный и q = p-1;

4) G - связный, но при удалении любого ребра становится несвязным;

5) G - без циклов, но при добавлении любого нового ребра на тех же вершинах появляется цикл.

Для представления данных в информационных системах, в справочниках, при реализации алгоритмов поиска и в других приложениях часто используются корневые деревья, то есть деревья с выделенной вершиной, именуемой корнем.

Определение. Подграф G₁ = (V₁,E₁) графа G = (V,E) называется остовным деревоми, если G₁ - дерево и множество его вершин совпадает V, т.е. V₁ = V.

Таким образом, о стовное дерево представляет собой связное подмножество графа, не содержащее циклов, включающее в себя все вершины графа и некоторые из его ребер.

Теорема. Любой (конечный) связный граф G = (V,E) содержит хотя бы одно остовное дерево G₁ = (V,E₁).

Граф называется взвешенным, если каждому его ребру 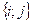приписан некоторый вес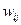

Весом остовного дерева называется сумма весов всех его ребер.

Минимальным остовным деревом (МОД) связного взвешенного графа называется его связный подграф, состоящий из всех вершин исходного дерева и некоторых его ребер, причем сумма весов ребер минимально возможная. Если исходный граф несвязен, то описываемую ниже процедуру можно применять поочередно к каждой его компоненте связности, получая тем самым минимальные остовные деревья для этих компонент.

 

Одно из применений минимальных остовных деревьев - организация внутренней компьютерной сети. Передающие станции устанавливаются в стратегически важных местах некоторой области. Если мы хотим уменьшить суммарную стоимость объединения станций в сеть, то можно нарисовать граф, в котором станции будут служить вершинами, а ребрам, их соединяющим, можно приписать стоимость соединения. Минимальное остовное дерево этого графа указывает, какие станции следует соединить между собой, чтобы любые две станции оказались соединенными, причем общая стоимость соединения была минимально возможной. Аналогичные приложения имеет и задача поиска кратчайшего пути в графе: умение решать такую задачу помогает планировать путь на автомобиле или посылать сообщение по компьютерной сети.

Алгоритм поиска минимального остовного дерева

МОД для связного графа можно найти с помощью грубой силы. Поскольку множество ребер МОД является подмножеством в множестве ребер исходного графа, можно просто перебрать все возможные подмножества и найти среди них МОД. Нетрудно видеть, что это чрезвычайно трудоемкий процесс. В множестве из N ребер имеется 2^N подмножеств. Алгоритм Дейкстры-Прима В конце 1950-х годов Эдгар Дейкстра и Прим, работая и публикуя свои результаты независимо друг от друга, предложили следующий алгоритм построения МОД. Воспользуемся для поиска МОД так называемым "жадным" алгоритмом. Жадные алгоритмы действуют, используя в каждый момент лишь часть исходных данных и принимая лучшее решение на основе этой части. В нашем случае мы будем на каждом шаге рассматривать множество ребер, допускающих присоединение к уже построенной части остовного дерева, и выбирать из них ребро с наименьшим весом. Повторяя эту процедуру, мы получим остовное дерево с наименьшим весом. Разобьем вершины графа на три класса: вершины, вошедшие в уже построенную часть дерева, вершины, окаймляющие построенную часть, и еще не рассмотренные вершины. Начнем с произвольной вершины графа и включим ее в остовное дерево. Поскольку результатом построения будет некорневое дерево, выбор исходной вершины не влияет на окончательный результат (конечно, если МОД единственно). Все вершины, соединенные с данной, заносим в кайму. Затем выполняется цикл поиска ребра с наименьшим весом, соединяющего уже построенную часть остовного дерева с каймой; это ребро вместе с новой вершиной добавляется в дерево и происходит обновление каймы. После того, как в дерево попадут все вершины, работа будет закончена.

 

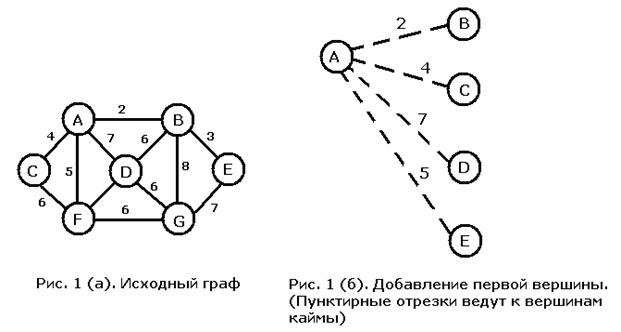
На рисунке 1 описано исполнение алгоритма на конкретном примере.

В начале процесса мы выбираем произвольный узел A. Как мы уже говорили, при другом выборе начальной вершины результат будет тем же самым, если МОД единственно.

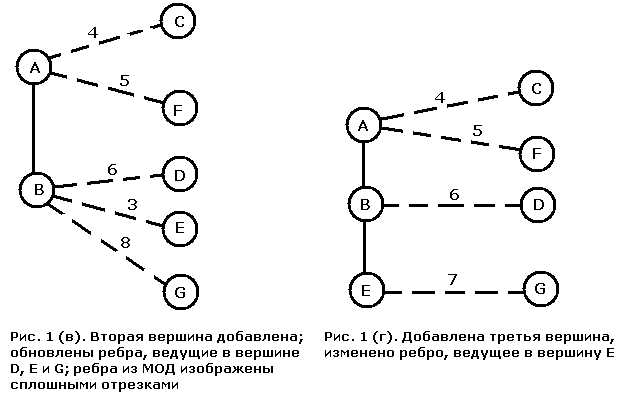
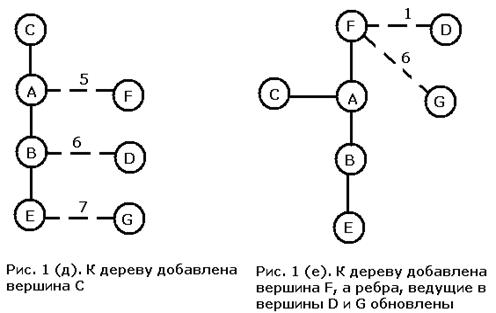
Исходный граф изображен на рис. 1 (а) и, как уже упоминалось, мы начинаем построение МОД с вершины A. Все вершины, непосредственно связанные с A, образуют исходную кайму. Видно, что ребро наименьшего веса связывает узлы A и B, поэтому к уже построенной части МОД добавляется вершина B вместе с ребром AB. При добавлении к дереву вершины B (рис. 1 (в)) мы должны определить, не следует ли добавить к кайме новые вершины. В результате мы обнаруживаем, что это необходимо проделать с вершинами E и G. Поскольку обе эти вершины соединены только с вершиной B уже построенной части дерева, мы добавляем соединяющие ребра к списку рассматриваемых на следующем шаге. Здесь же необходимо проверить, являются ли ребра, ведущие из вершины A в C, D и F, кратчайшими среди ребер, соединяющих эти вершины с деревом, или есть более удобные ребра, исходящие из B. В исходном графе вершина B не соединена непосредственно ни с C, ни с F, поэтому для них ничего не меняется. А вот ребро BD короче ребра AD, и поэтому должно его заменить. Наименьший вес из пяти ребер, идущих в кайму, имеет ребро BE, поэтому к дереву нужно добавить его и вершину E (рис. 1 (г)). Вес ребра EG меньше веса ребра BG, поэтому оно замещает последнее. Из четырех ребер, ведущих в кайму, наименьший вес имеет AC, поэтому следующим к дереву добавляется оно. Добавление к остовному дереву вершины C и ребра AC (рис. 1 (д)) не приводит к изменению списка ребер.

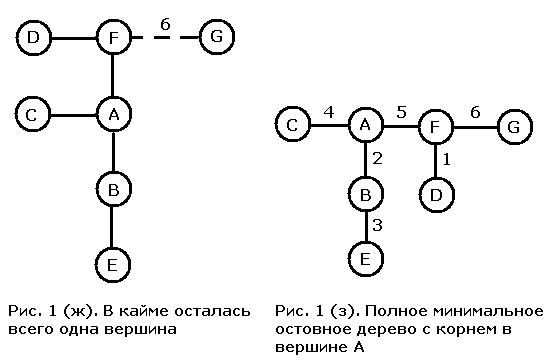
Затем мы выбираем ребро AF и добавляем его к дереву вместе с вершиной F. Кроме того, мы меняем список связей, поскольку вес ребра FD меньше веса ребра BD, а вес ребра FG меньше веса ребра EG. В получившейся кайме (рис. 1 (е)) ребро FD имеет наименьший вес среди оставшихся, и оно добавляется следующим.

Теперь осталось добавить к дереву всего один узел (рис. 1 (ж)). После этого процесс завершается, и мы построили МОД с корнем в вершине A (рис. 1 (з)).

Алгоритм Крускала

Алгоритм Дейкстры-Прима начинает построение МОД с конкретной вершины графа и постепенно расширяет построенную часть дерева; в отличие от него алгоритм Крускала делает упор на ребрах графа.

В этом алгоритме мы начинаем с пустого дерева и добавляем к нему ребра в порядке возрастания их весов пока не получим набор ребер, объединяющий все вершины графа. Если ребра закончатся до того, как все вершины будут соединены между собой, то это означает, что исходный граф был несвязным, и полученный нами результат представляет собой объединение МОД всех его компонент связности.

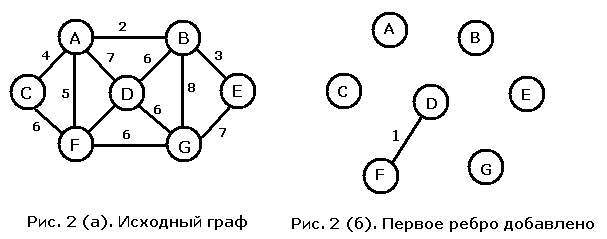
Мы работаем с тем же графом (см. рис. 2 (а)), что и при описании алгоритма Дейкстры -Прима. Начнем с ребра наименьшего веса, то есть с ребра DF. Начальная ситуация изображена на рис. 2 (б).

Следующим добавляется ребро веса 2, соединяющее вершины A и B (рис. 2 (в)), а затем - ребро веса три, и мы получаем ситуацию с рис. 2 (г).

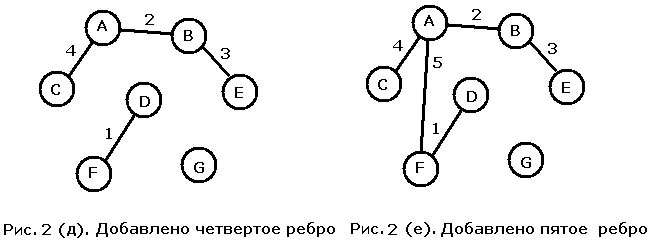
К результирующему графу последовательно добавляются ребра весов 4 и 5 (рисунки 2 (д) и (е)). Несоединенной осталась лишь вершина G. Следующими мы должны рассмотреть ребра веса 6.

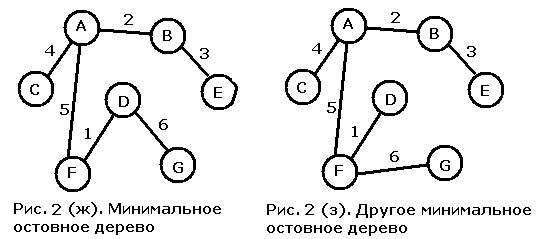
Два из четырех ребер веса 6 следует отбросить, поскольку их добавление приведет к появлению цикла в уже построенной части МОД. Присоединение ребра CF создало бы цикл, содержащий вершину A, а присоединение ребра BD - цикл, содержащий вершины A и F. Обе оставшиеся возможности подходят в равной степени, и, выбирая одну из них, мы получаем либо МОД с рис. 2 (ж), либо МОД с рис. 2 (з).