Мгновенный центр скоростей
3.2.3 Мгновенный центр скоростей (МЦС)
Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра. В соответствии с этим легко доказывается, что при плоско-параллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нолю. Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например PV, CV.
При определении положения МЦС скорость любой точки может быть записана: VM=VCV+VMCV, где точка СV выбрана за полюс. Поскольку это МЦС и VCV=0, то скорость любой точки определяется как скорость вращении вокруг мгновенного центра скоростей.
 Из рис. 1.5 видно, что мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных к скоростям точек, при этом всегда справедливо соотношение
Из рис. 1.5 видно, что мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных к скоростям точек, при этом всегда справедливо соотношение

 Рис. 1.5
На нижеприведенных рисунках показаны примеры определения положения мгновенного центра скоростей и приведены формулы для расчета скоростей точек.
Рис. 1.5
На нижеприведенных рисунках показаны примеры определения положения мгновенного центра скоростей и приведены формулы для расчета скоростей точек.
 Для рисунка 1.6:
1. СV совпадает с точкой В VB=0. Шатун АВ вращается вокруг точки В
Для рисунка 1.6:
1. СV совпадает с точкой В VB=0. Шатун АВ вращается вокруг точки В
 2.
2.
 3. МЦС лежит в «бесконечности»
3. МЦС лежит в «бесконечности»
 4.
4.
 Рис. 1.6
Рис. 1.6
 
 Рис. 1.7
Рис. 1.7
 Рис. 1.8
здесь VB II VA
В этом случае МЦС находится в “бесконечности”, т.е
Рис. 1.8
здесь VB II VA
В этом случае МЦС находится в “бесконечности”, т.е


 Рис. 1.9
Формулы справедливы при отсутствии проскальзывания в точке СV.
Рис. 1.9
Формулы справедливы при отсутствии проскальзывания в точке СV.
 
 Рис. 1.10
Рис. 1.10
| Теоретическая механика Содержание краткой теории Примеры решения задач Обзорный курс |
Теорема существования и единственности решения задачи Коши
Укажем достаточные условия существования и единственности решения задачи Коши
 . (1)
. (1)
Теорема Пикара. Пусть функция непрерывна в прямоугольнике

и удовлетворяет условию Липшица по y равномерно относительно x, т.е.  , для всех x,
, для всех x,  и
и  .
.
Пусть
 ,
,
тогда задача Коши (1) на промежутке  имеет единственное решение
имеет единственное решение  .
.
Замечание. Условие Липшица в теореме Пикара можно заменить на требование ограниченности или непрерывности  в каждом компакте из области определения дифференциального уравнения.
в каждом компакте из области определения дифференциального уравнения.
Решение задачи Коши при выполнении условий теоремы Пикара можно найти как предел при  равномерно сходящейся последовательности функций
равномерно сходящейся последовательности функций  , определяемых рекуррентным соотношением
, определяемых рекуррентным соотношением
 . (2)
. (2)
Оценка погрешности, получаемой при замене точного решения y(x) n- м приближением  , выражается неравенством
, выражается неравенством
 .
.
Теорема Пеано. Пусть функция непрерывна в прямоугольнике 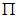 , причем
, причем
 .
.
Тогда задача Коши на промежутке  имеет по крайне мере одно решение
имеет по крайне мере одно решение  .
.
Система уравнений

в векторных обозначениях записывается в виде
 , (3)
, (3)
где  и
и  - векторы. Непрерывность вектор - функции f означает непрерывность всех функций
- векторы. Непрерывность вектор - функции f означает непрерывность всех функций  , а вместо
, а вместо  рассматривается матрица из частных производных
рассматривается матрица из частных производных  .
.
Рассмотренные выше теоремы остаются справедливы и для системы, записанной в виде (3). При этом |y| означает длину вектора y:  .
.
Рассмотрим уравнение вида
 . (4)
. (4)
Пусть в области D функция f и ее частные производные первого порядка по  непрерывны, и точка
непрерывны, и точка  лежит внутри D. Тогда при начальных условиях
лежит внутри D. Тогда при начальных условиях

уравнение (4) имеет единственное решение.
Уравнение (4) можно свести к системе вида (2), если ввести новые неизвестные функции по формулам  . Тогда уравнение (4) сводится к системе
. Тогда уравнение (4) сводится к системе
 ,
,
которая является частным случаем системы (3) и к которой применимы все рассмотренные утверждения.
Часто решение задачи Коши существует не только на отрезке, указанном в теоремах, но и на большем отрезке.
Если функция f(x,y) удовлетворяет в прямоугольнике 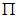 условиям теоремы Пикара, то всякое ее решение
условиям теоремы Пикара, то всякое ее решение  можно продолжить до выхода на границу прямоугольника
можно продолжить до выхода на границу прямоугольника 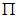 . Если функция f(x,y) в полосе
. Если функция f(x,y) в полосе  непрерывна и удовлетворяет неравенству
непрерывна и удовлетворяет неравенству  , где a(x) и b(x) - непрерывные функции, то всякое решение уравнения (1) и (3) можно продолжить на весь интервал
, где a(x) и b(x) - непрерывные функции, то всякое решение уравнения (1) и (3) можно продолжить на весь интервал  .
.
Пример 1. Построить последовательные приближения  к решению данного уравнения с данными начальными условиями:
к решению данного уравнения с данными начальными условиями:  .
.
Решение.
Последовательные приближения к решению данной задачи определим по рекуррентной формуле
 .
.
Подставляя в последнюю формулу поочередно n=0,1 найдем нужные приближения:
 ,
,
 .
.
Пример 2. Указать какой-нибудь отрезок, на котором существует решение с данными начальными условиями:  .
.
Решение.
Воспользуемся теоремой Пикара. В данном случае  . Функция f непрерывна в любом прямоугольнике
. Функция f непрерывна в любом прямоугольнике 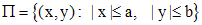 и удовлетворяет условию Липшица, поскольку производная
и удовлетворяет условию Липшица, поскольку производная  ограничена числом
ограничена числом  . Следовательно, на сегменте
. Следовательно, на сегменте  , где
, где

существует единственное решение данной задачи. Найдем число
 .
.
Ясно, что если на каком - то сегменте I существует единственное решение, то оно существует и на меньшем сегменте, вложенном в I. Отсюда следует, что желательно найти как можно больший отрезок I, т.е.
 .
.
Так как функция  возрастает при
возрастает при  , а функция
, а функция  убывает, то
убывает, то  достигается при условии, что
достигается при условии, что 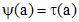 , т.е.
, т.е.
 . (5)
. (5)
Взяв производную по b от правой части (5), найдем, что при  достигается максимум a, который легко вычислить, подставив значение
достигается максимум a, который легко вычислить, подставив значение  в (5). Тогда получим
в (5). Тогда получим
 .
.
Таким образом, можно гарантировать существование и единственность решения данной задачи на сегменте  .
.
Пример 3. При каких начальных условиях существует единственное решение уравнения  .
.
Решение.
Поскольку функция

вместе с частными производными

непрерывна при  и
и  , то через каждую точку
, то через каждую точку  , где
, где 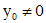 и
и  , проходит единственная интегральная кривая уравнения
, проходит единственная интегральная кривая уравнения
 .
.