ПРЕДИСЛОВИЕ
Цифровая обработка сигналов (ЦОС), как одно из наиболее динамично развиваемых и перспективных направлений, имеет большое фундаментальное и прикладное значение в современной радиотехнике. Удельный вес ЦОС в радиоэлектронных устройствах и системах по мере повышения ее быстродействия и снижения стоимости все более возрастает. Ее методы используются для разработки и исследования радиоэлектронных устройств и систем различного назначения, а ее средства – для их аппаратно-программной реализации. Обучение методам и средствам ЦОС осуществляется в рамках дисциплины «Цифровая обработка сигналов». Она охватывает широкий круг теоретических вопросов, изучаемых на лекционных и лабораторных занятиях и в процессе самостоятельной работы студентов.
Лабораторный практикум (часть I) включает изучение базовых вопросов дискретизации сигналов по времени и их цифрового представления, спектрального анализа дискретных сигналов, применения методов ЦОС в различных радиоэлектронных системах.
Лабораторный практикум предназначен для студентов, обучающихся по специальности «Радиоэлектронные системы и комплексы», а также бакалаврам и магистрантам по направлениям подготовки «Радиотехника» и «Биотехнические системы», в образовательных программах которых предусмотрено изучение дисциплины «Цифровая обработка сигналов».
Лабораторная работа №1
Дискретизация сигналов
Цель работы. Изучить вопросы аналогово-цифрового и цифро-аналогового преобразования сигналов. Исследовать процедуру дискретизации и восстановления аналоговых сигналов.
Теоретические сведения
Аналоговый сигнал  является вещественнозначной функцией вещественного непрерывного аргумента (времени) источниками которого являются различные физические процессы и явления, непрерывно меняющиеся во времени (или в пространстве).
является вещественнозначной функцией вещественного непрерывного аргумента (времени) источниками которого являются различные физические процессы и явления, непрерывно меняющиеся во времени (или в пространстве).
Дискретный сигнал  – это кусочно-непрерывная вещественнозначная функция дискретного аргумента
– это кусочно-непрерывная вещественнозначная функция дискретного аргумента  . Дискретный сигнал представляет собой набор отсчетов некоторой величины, измеренной в дискретные моменты времени. Интервал
. Дискретный сигнал представляет собой набор отсчетов некоторой величины, измеренной в дискретные моменты времени. Интервал  между двумя соседними отсчетами называется шагом дискретизации, а обратная величина
между двумя соседними отсчетами называется шагом дискретизации, а обратная величина  частотой дискретизации (или
частотой дискретизации (или  круговая частота дискретизации).
круговая частота дискретизации).
Устройства, преобразующие аналоговый сигнал в цифровой, называется аналогово-цифровым преобразователем (АЦП). Обратное преобразование цифровых сигналов в аналоговые выполняется цифро-аналоговым преобразователем (ЦАП).
Основными характеристиками АЦП являются шаг дискретизации по времени (или частота дискретизация) и шаг квантования по уровню (или разрядность). Под разрядностью понимается число двоичных разрядов  используемых для записи одно квантованного значения.
используемых для записи одно квантованного значения.
Дискретный сигнал можно получить из аналогового посредством процедуры дискретизации во времени. В этом случае дискретные сигнал  представляет собой последовательность отсчетов, значения которых в точности равны значениям исходного аналогового сигнала в дискретные моменты времени
представляет собой последовательность отсчетов, значения которых в точности равны значениям исходного аналогового сигнала в дискретные моменты времени  . Так как отсчеты сигнала представляют собой конечный набор отсчетов, их можно пронумеровать целыми числами.
. Так как отсчеты сигнала представляют собой конечный набор отсчетов, их можно пронумеровать целыми числами.
Цифровой сигнал 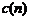 – сигнал дискретный и по времени и по значениям. Цифровой сигнал может быть получен из дискретного путем процедуры квантования по уровню.
– сигнал дискретный и по времени и по значениям. Цифровой сигнал может быть получен из дискретного путем процедуры квантования по уровню.
Таким образом, чтобы получить из аналогового сигнала цифровой необходимо провести процедуру дискретизации по времени и квантования по уровню. В результате мы получим вместо непрерывного сигнала, последовательность целых чисел.
Математически дискретный сигнал определяют:
· функцией дискретного времени  , соответствующей выборкам аналогового сигнала в дискретные равноотстоящие моменты времени:
, соответствующей выборкам аналогового сигнала в дискретные равноотстоящие моменты времени:

· функцией номера выборки  , в общем случае не связанной с временем:
, в общем случае не связанной с временем:
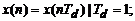
· функцией непрерывного времени  , получаемой умножением аналогового сигнала
, получаемой умножением аналогового сигнала  на дискретизирующую
на дискретизирующую  в виде периодической последовательности
в виде периодической последовательности 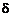 -импульсов с периодом повторения
-импульсов с периодом повторения  , где
, где  –
– 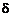 -импульс бесконечной амплитуды, нулевой длительности и единичной площади
-импульс бесконечной амплитуды, нулевой длительности и единичной площади  , задержанный на
, задержанный на  отсчетов и имеющий размерность частоты или
отсчетов и имеющий размерность частоты или  . Графически дискретные сигналы представляются функцией дискретного времени
. Графически дискретные сигналы представляются функцией дискретного времени  или номера выборки
или номера выборки  (рис. 1.1).
(рис. 1.1).
·
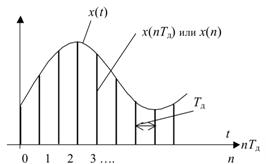
Рис. 1.1. Графики непрерывного  и дискретного
и дискретного  сигналов
сигналов
Сигналы, определяемые функцией номера выборки  , называют также числовыми, или дискретными, последовательностями. Приводимую на графиках функцию непрерывного времени отождествляют либо с аналоговым сигналом
, называют также числовыми, или дискретными, последовательностями. Приводимую на графиках функцию непрерывного времени отождествляют либо с аналоговым сигналом  , соответствующим дискретному сигналу
, соответствующим дискретному сигналу  , либо с некоторой условной огибающей дискретной последовательности
, либо с некоторой условной огибающей дискретной последовательности  , более наглядно отображающей ее функциональную зависимость.
, более наглядно отображающей ее функциональную зависимость.
При дискретизации аналогового сигнала с финитным спектром, ограниченным максимальной частотой  , отвечающей условию
, отвечающей условию  (рис. 1.2), спектр дискретного сигнала
(рис. 1.2), спектр дискретного сигнала  в основной полосе частот
в основной полосе частот  (при
(при  ) точно совпадает (до постоянного множителя
) точно совпадает (до постоянного множителя  ) со спектром аналогового сигнала:
) со спектром аналогового сигнала:  . Условие
. Условие  (или
(или  ) отвечает теореме отсчетов Котельникова.
) отвечает теореме отсчетов Котельникова.

Рис. 1.2. Спектральные преобразования при дискретизации аналогового сигнала с финитным спектром при 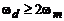
В этом случае возможно точное восстановление аналогового сигнала  по его дискретным выборкам
по его дискретным выборкам  с помощью идеального фильтра-интерполятора нижних частот (ФНЧ) с прямоугольной частотной характеристикой
с помощью идеального фильтра-интерполятора нижних частот (ФНЧ) с прямоугольной частотной характеристикой  равной 1 при
равной 1 при 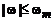 и равной нулю при
и равной нулю при  (на рис. 1.2
(на рис. 1.2  ). Сигнал на выходе ФНЧ соответствует обратному преобразованию Фурье депериодизированного спектра дискретного сигнала
). Сигнал на выходе ФНЧ соответствует обратному преобразованию Фурье депериодизированного спектра дискретного сигнала 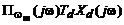 , имеющего размерность спектральной плотности:
, имеющего размерность спектральной плотности:
 .
.
Подставив сюда  и заменив для общности
и заменив для общности  на
на  , получим
, получим
 . (1.1)
. (1.1)
Выражение (1.1) является разложением аналогового сигнала  в ряд по базисным интерполирующим функциям
в ряд по базисным интерполирующим функциям 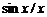 (или
(или  ) с весовыми коэффициентами
) с весовыми коэффициентами  (ряд Котельникова). В соответствии с ним и осуществляется математически восстановление аналогового сигнала по его дискретным выборкам.
(ряд Котельникова). В соответствии с ним и осуществляется математически восстановление аналогового сигнала по его дискретным выборкам.
При квантовании по уровню бесконечное множество возможных значений дискретного сигнала  в заданном максимальном диапазоне его изменения
в заданном максимальном диапазоне его изменения  замещается конечным числом уровней квантования
замещается конечным числом уровней квантования  дискретного квантованного сигнала
дискретного квантованного сигнала 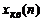 . С одним из них в соответствии с определенным правилом или алгоритмом и отождествляется точное мгновенное значение дискретного сигнала
. С одним из них в соответствии с определенным правилом или алгоритмом и отождествляется точное мгновенное значение дискретного сигнала  (рис. 1.3).
(рис. 1.3).

Рис. 1.3. Иллюстрация квантования сигнала по уровню
Интервал между уровнями квантования называется шагом квантования по уровню 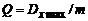 .
.
Квантование возможно с усечением и с округлением. Квантованный дискретный сигнал 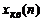 определяется при усечении как
определяется при усечении как
 , (1.2)
, (1.2)
при округлении как
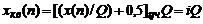 , (1.3)
, (1.3)
где  − это целая часть заключенного в скобки отношения, соответствующая номеру уровня квантования, с которым отождествляется точное значение квантуемого дискретного сигнала: с ближайшим меньшим − при усечении и ближайшим – при округлении. Для однополярного сигнала
− это целая часть заключенного в скобки отношения, соответствующая номеру уровня квантования, с которым отождествляется точное значение квантуемого дискретного сигнала: с ближайшим меньшим − при усечении и ближайшим – при округлении. Для однополярного сигнала 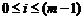 , для двухполярного
, для двухполярного  .
.
Номер уровня квантования  при известном значении шага квантования
при известном значении шага квантования 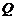 однозначно определяет значение дискретного квантованного сигнала и, следовательно, является его цифровым (числовым) эквивалентом. Представленный в двоичном коде (
однозначно определяет значение дискретного квантованного сигнала и, следовательно, является его цифровым (числовым) эквивалентом. Представленный в двоичном коде ( ), он соответствует цифровому сигналу на выходе АЦП
), он соответствует цифровому сигналу на выходе АЦП  . Число двоичных разрядов АЦП
. Число двоичных разрядов АЦП  связано с числом уровней квантования
связано с числом уровней квантования  соотношением
соотношением  . Например, для 10-разрядного АЦП
. Например, для 10-разрядного АЦП  , для АЦП разрядностью 12 бит −
, для АЦП разрядностью 12 бит −  и т.д.
и т.д.
Получаемый двоичный код двухполярного АЦП представляет собой целое число со знаком в прямом или дополнительном коде. Такое представление соответствует целочисленному кодированию цифрового сигнала. Оно осуществляется в соответствии с алгоритмом
 . (1.4)
. (1.4)
Разряды целочисленного кода  (рис. 1.4, а) имеют веса, убывающие от
(рис. 1.4, а) имеют веса, убывающие от  (старший знаковый разряд) до
(старший знаковый разряд) до  (младший разряд);
(младший разряд);  – число разрядов или бит цифрового сигнала без учета знакового разряда.
– число разрядов или бит цифрового сигнала без учета знакового разряда.
Наряду с целочисленным в цифровой обработке сигналов широко используется представление двоичных чисел правильными дробями – так называемое дробное кодирование цифрового сигнала. Оно обеспечивает простое ограничение их разрядности в процессе обработки путем отбрасывания (усечения или округления) лишних младших разрядов.
Дробное представление цифрового сигнала АЦП получается в соответствии с алгоритмом
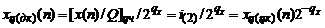 . (1.5)
. (1.5)
Значения сигнала при этом не превышают по модулю 1 и заключены в пределах:  ; веса его разрядов убывают от
; веса его разрядов убывают от  (знаковый разряд) до
(знаковый разряд) до  (младший значащий разряд) (рис. 1.4, б).
(младший значащий разряд) (рис. 1.4, б).


а б
Рис. 1.4. Целочисленное (а) и дробное (б) представление цифрового сигнала
Таким образом, дробное и целочисленное представления цифрового сигнала отличаются только интерпретацией весов разрядов двоичного кода и связаны соотношениями
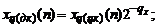
 .
.
Код АЦП при дробном представлении с фиксированной точкой преобразуется к стандартному формату кодов процессора ЦОС (слово, двойное слово, расширенное слово) путем дополнения его справа недостающим числом нулевых бит.
Значение квантованного сигнала в вольтах можно найти по его цифровому коду как  (вольт).
(вольт).
Например: при 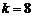 (восьмиразрядное АЦП) можно отобразить
(восьмиразрядное АЦП) можно отобразить  целых чисел: от 0 до 255. Максимальная амплитуда сигнала на входе АЦП
целых чисел: от 0 до 255. Максимальная амплитуда сигнала на входе АЦП  является фиксированной и также является характеристикой АЦП. Весь динамический диапазон значений входного сигнала простирается от
является фиксированной и также является характеристикой АЦП. Весь динамический диапазон значений входного сигнала простирается от  до
до  . Этот диапазон делится на 256 уровней, тогда шаг квантования будет равен
. Этот диапазон делится на 256 уровней, тогда шаг квантования будет равен 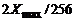 . Следовательно, связь между разрядностью и шагом квантования:
. Следовательно, связь между разрядностью и шагом квантования:  .
.
Восстановление аналогового сигнала из дискретного возможно если шаг дискретизации удовлетворяет теореме Котельникова.
Практическая часть
1. Провести исследование восстановления сигнала из дискретной и цифровой выборки в зависимости от шага дискретизации. Параметры сигнала в соответствии с вариантом представлены в табл. 1.1. Построить графики исходного (аналогового), дискретизированного, цифрового и восстановленного сигналов для нескольких значений частоты дискретизации и числа уровней квантования (разрядности 8, 12, 16).
2. Исследовать зависимости погрешности восстановления сигналов от частоты дискретизации и числа уровней квантования (разрядности).
Таблица 1.1
| № вар | Параметры сигналов | |||
| Полигармонический сигнал | АМ сигнал | Последовательность прямоугольных импульсов | Последовательность треугольных импульсов | |
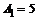 , ,  , ,  , ,  Гц, Гц,  Гц, Гц,  Гц. Гц.
|  , ,  , , 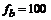 Гц, Гц,  Гц. Гц.
|  , ,  Гц, Гц,  . .
|  , ,  Гц. Гц.
| |
 , ,  , , 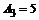 , ,  Гц, Гц,  Гц, Гц, 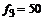 Гц. Гц.
|  , ,  , ,  Гц, Гц,  Гц. Гц.
|  , ,  Гц, Гц, 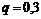 . .
| 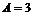 , ,  Гц. Гц.
| |
 , ,  , ,  , ,  Гц, Гц,  Гц, Гц, 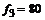 Гц. Гц.
| 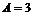 , ,  , ,  Гц, Гц,  Гц. Гц.
|  , ,  Гц, Гц,  . .
| 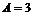 , , 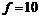 Гц. Гц.
| |
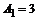 , ,  , , 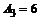 , , 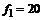 Гц, Гц,  Гц, Гц,  Гц. Гц.
|  , ,  , ,  Гц, Гц,  Гц. Гц.
|  , ,  Гц, Гц, 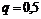 . .
| 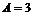 , ,  Гц. Гц.
| |
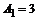 , ,  , , 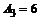 , ,  Гц, Гц,  Гц, Гц, 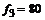 Гц. Гц.
|  , , 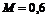 , ,  Гц, Гц,  Гц. Гц.
|  , ,  Гц, Гц,  . .
| 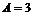 , ,  Гц. Гц.
| |
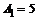 , ,  , ,  , ,  Гц, Гц,  Гц, Гц,  Гц. Гц.
|  , ,  , ,  Гц, Гц,  Гц. Гц.
|  , ,  Гц, Гц,  . .
|  , ,  Гц. Гц.
| |
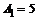 , ,  , ,  , ,  Гц, Гц,  Гц, Гц,  Гц. Гц.
|  , ,  , , 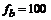 Гц, Гц,  Гц. Гц.
|  , ,  Гц, Гц,  . .
|  , ,  Гц. Гц.
| |
 , ,  , , 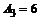 , ,  Гц, Гц,  Гц, Гц, 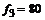 Гц. Гц.
|  , , 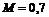 , , 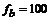 Гц, Гц,  Гц. Гц.
|  , ,  Гц, Гц,  . .
|  , ,  Гц. Гц.
| |
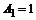 , ,  , ,  , ,  Гц, Гц,  Гц, Гц,  Гц. Гц.
|  , ,  , ,  Гц, Гц,  Гц. Гц.
|  , ,  Гц, Гц,  . .
|  , ,  Гц. Гц.
| |
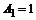 , ,  , ,  , , 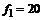 Гц, Гц,  Гц, Гц, 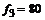 Гц. Гц.
|  , ,  , ,  Гц, Гц,  Гц. Гц.
|  , ,  Гц, Гц, 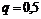 . .
|  , ,  Гц. Гц.
| |
 , ,  , ,  , ,  Гц, Гц,  Гц, Гц, 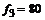 Гц. Гц.
|  , , 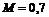 , ,  Гц, Гц,  Гц. Гц.
|  , ,  Гц, Гц, 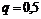 . .
|  , ,  Гц. Гц.
| |
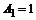 , ,  , ,  , ,  Гц, Гц,  Гц, Гц,  Гц. Гц.
|  , ,  , ,  Гц, Гц,  Гц. Гц.
|  , ,  Гц, Гц,  . .
|  , ,  Гц. Гц.
|
Контрольные вопросы
1. Какие преобразования имеют место при цифровой обработке сигналов?
2. Что такое дискретный сигнал и дискретная последовательность?
3. Из каких условий выбирается частота дискретизации аналоговых сигналов?
4. Какова математическая модель квантования сигнала по уровню?
5. Как осуществляется цифровое кодирование сигнала?
6. Сформулируйте теорему Котельникова.
7. При каких условиях возможно точное восстановление аналогового сигнала по его дискретным выборкам?
Лабораторная работа №2
Спектр дискретных сигналов
Цель работы. Изучить вопросы спектрального анализа дискретных сигналов. Исследовать алгоритмы дискретного преобразования Фурье.
Теоретические сведения
Дискретное преобразование Фурье (ДПФ) является базовым алгоритмом цифровой обработки сигналов в частотной области. Благодаря наличию эффективных алгоритмов его вычисления – алгоритмов быстрого преобразования Фурье (БПФ) – ДПФ широко используется для целей цифровой фильтрации и спектрально-корреляционного анализа сигналов.
Дискретное преобразование Фурье (ДПФ), соответствует выборкам непрерывного преобразования Фурье  дискретной последовательности
дискретной последовательности  конечной длины
конечной длины  , вычисленным на дискретных равностоящих частотах
, вычисленным на дискретных равностоящих частотах 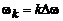 (рис. 2.1):
(рис. 2.1):
 , (2.1)
, (2.1)
где  – шаг дискретизации по частоте;
– шаг дискретизации по частоте;  – число вычисляемых частотных выборок ДПФ в полосе частот
– число вычисляемых частотных выборок ДПФ в полосе частот  , в общем случае не равное
, в общем случае не равное  ;
;  – номер частотной выборки.
– номер частотной выборки.
В соответствии с числом вычисляемых частотных выборок  ДПФ называют
ДПФ называют  -точечным и представляют как в виде функции (2.1) дискретной частоты
-точечным и представляют как в виде функции (2.1) дискретной частоты  , так и номера частотной выборки
, так и номера частотной выборки  :
:
 ,
,
 . (2.2)
. (2.2)

Рис. 2.1. Дискретизация сигнала в частотной области
Выбор шага дискретизации по частоте при вычислении ДПФ определяется возможностью восстановления сигнала  и его непрерывного спектра
и его непрерывного спектра  по частотным выборкам ДПФ.
по частотным выборкам ДПФ.
Восстановление сигнала по дискретизированному по частоте спектру осуществляется с помощью обратного ДПФ (ОДПФ). Как и прямое ДПФ (2.1), ОДПФ может быть получено путем дискретизации по частоте непрерывного обратного преобразования Фурье:
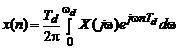 .
.
Используя замены  ;
; 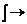 ∑;
∑; 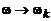 , находим
, находим
 . (2.3)
. (2.3)
Сигнал  периодичен с периодом
периодичен с периодом  :
:  ,
, 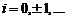 Он является периодическим повторением сигнала
Он является периодическим повторением сигнала  :
: 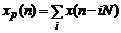 , так как дискретизация сигнала в частотной области приводит к его периодизации во временной.
, так как дискретизация сигнала в частотной области приводит к его периодизации во временной.
При  ,
, 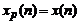 ,
,  – сигнал
– сигнал  на интервале
на интервале  точно совпадает с исходным сигналом
точно совпадает с исходным сигналом  , дополненным
, дополненным  нулевыми отсчетами, периодически продолжаясь за пределами этого интервала (рис. 2.2).
нулевыми отсчетами, периодически продолжаясь за пределами этого интервала (рис. 2.2).

Рис. 2.2. Сигнал, соответствующий ОДПФ при 
ОДПФ, вычисляемое на интервале  , обеспечивает в этом случае точное восстановление сигнала
, обеспечивает в этом случае точное восстановление сигнала  по его ДПФ.
по его ДПФ.
При  (
(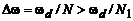 ) имеет место перекрытие периодизированных с периодом
) имеет место перекрытие периодизированных с периодом  последовательностей
последовательностей  (явление наложения во временной области), так что
(явление наложения во временной области), так что  при
при  (рис. 2.3). Это исключает возможность точного восстановления сигнала по его дискретизированному спектру.
(рис. 2.3). Это исключает возможность точного восстановления сигнала по его дискретизированному спектру.

Рис. 2.3. Сигнал, соответствующий ОДПФ при 
Соотношение  определяет условие выбора шага дискретизации по частоте
определяет условие выбора шага дискретизации по частоте  , которое отвечает также теореме Котельникова в частотной области: спектр сигнала конечной длительности может быть точно восстановлен по его частотным выборкам, взятым с вышеуказанным шагом по частоте
, которое отвечает также теореме Котельникова в частотной области: спектр сигнала конечной длительности может быть точно восстановлен по его частотным выборкам, взятым с вышеуказанным шагом по частоте  .
.
Вычисление ДПФ по числу точек  , превышающему длину последовательности
, превышающему длину последовательности  (дополняемую в этом случае (
(дополняемую в этом случае ( ) нулевыми отсчетами), эквивалентно интерполяции по частоте спектра, дискретизированного с максимально возможным шагом
) нулевыми отсчетами), эквивалентно интерполяции по частоте спектра, дискретизированного с максимально возможным шагом 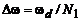 . Дополнение
. Дополнение  нулевыми отсчетами используется для повышения частотного разрешения ДПФ.
нулевыми отсчетами используется для повышения частотного разрешения ДПФ.
Таким образом,  -точечное ДПФ соответствует спектру периодизированной с периодом
-точечное ДПФ соответствует спектру периодизированной с периодом  исходной последовательности
исходной последовательности  конечной длины
конечной длины 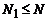 . ДПФ совпадает также с дискретным рядом Фурье периодической последовательности
. ДПФ совпадает также с дискретным рядом Фурье периодической последовательности  с периодом
с периодом  , имеющей линейчатый спектр.
, имеющей линейчатый спектр.
ОДПФ (2.3), вычисляемое по  частотным выборкам (
частотным выборкам ( -точечное ОДПФ), как и ДПФ (2.2) представляют также функцией номера частотной выборки
-точечное ОДПФ), как и ДПФ (2.2) представляют также функцией номера частотной выборки  :
:
 ,
,
 . (2.4)
. (2.4)
Множитель  может присутствовать в выражении либо ОДПФ, либо ДПФ.
может присутствовать в выражении либо ОДПФ, либо ДПФ.
Вычисление ОДПФ и ДПФ в соответствии с (2.2), (2.4) требует (при  )
)  операций умножения и
операций умножения и  операций сложения комплексных чисел. Оба преобразования используют единый вычислительный алгоритм, основанный на их достаточно простой взаимосвязи:
операций сложения комплексных чисел. Оба преобразования используют единый вычислительный алгоритм, основанный на их достаточно простой взаимосвязи:
 ,
,
где 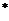 − операция комплексного сопряжения.
− операция комплексного сопряжения.
ДПФ обладает всеми свойствами непрерывного (по частоте  ) преобразования Фурье дискретных последовательностей, в том числе его периодичностью и симметрией.
) преобразования Фурье дискретных последовательностей, в том числе его периодичностью и симметрией.
Наиболее важной для цифровой фильтрации является связь ДПФ и свертки дискретных последовательностей. Линейная свертка определяется для конечных последовательностей 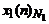 длиной
длиной  и
и  длиной
длиной 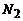 :
:

 .
.
Сигнал линейной свертки 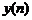 (рис. 2.4) имеет длину
(рис. 2.4) имеет длину 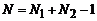 . Чтобы применить в данном случае теорему о свертке, ДПФ последовательностей
. Чтобы применить в данном случае теорему о свертке, ДПФ последовательностей 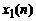 и
и  необходимо вычислить по одинаковому числу точек
необходимо вычислить по одинаковому числу точек  , соответствующему длине последовательности
, соответствующему длине последовательности 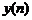 , с одинаковым шагом дискретизации по частоте
, с одинаковым шагом дискретизации по частоте  , т.е.
, т.е.

или
 ,
,  .
.
При этом последовательности 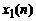 и
и  дополняются
дополняются  ,
, 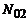 нулевыми отсчетами:
нулевыми отсчетами:
 ,
,  ,
,
что обеспечивает в частотной области интерполяцию их дискретизированного спектра.

Рис. 2.4. Иллюстрация ДВС
Сигнал 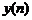 в соответствии с данным свойством также может быть определен с помощью ОДПФ от произведения
в соответствии с данным свойством также может быть определен с помощью ОДПФ от произведения  -точечных ДПФ свертываемых последовательностей
-точечных ДПФ свертываемых последовательностей 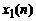 ,
,  :
:
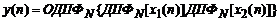 (2.5)
(2.5)
или
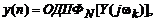
 .
.
Выражение (2.5) представляет алгоритм вычисления линейной свертки конечных последовательностей в частотной области. При использовании рассматриваемых далее алгоритмов быстрого преобразования Фурье его называют также алгоритмом быстрой свертки. Очевидно, что ДПФ линейной свертки последовательностей конечной длины 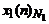 ,
,  эквивалентно ДПФ круговой свертки последовательностей, полученных путем периодизации их с периодом
эквивалентно ДПФ круговой свертки последовательностей, полученных путем периодизации их с периодом