Передаточная функция аналоговой системы определяется отношением преобразований Лапласа ее выходного и входного сигналов: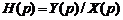 
. Операторное представление описывающих такие системы дифференциального уравнения и интеграла свертки дает общие выражения для передаточных функций аналоговых систем, соответственно, в виде дробнорациональной функции комплексной переменной 
:
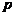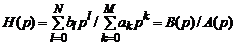(3.1)
и в виде преобразования Лапласа импульсной характеристики системы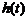 
:
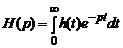. (3.2)
Корням полиномов числителя 
и знаменателя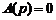 
передаточной функции (3.1) соответствуют нули 
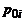и полюсы 
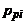системы, через которые передаточная функция представляется в так называемой нуль−полюсной форме:
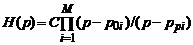, (3.3)
где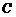 
– нормирующая константа.
По передаточной функции аналоговой системы непосредственно находится ее частотная характеристика:
,
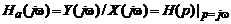которая в соответствии с (3.2) выражается и как Фурье-преобразование ее импульсной характеристики:
.
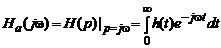Передаточной функцией дискретной системы называется отношение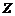 
-образов выходного и входного сигналов системы:
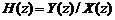. (3.4)
Конкретные ее выражения, получаемые 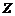-преобразованием разностных уравнений
,
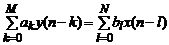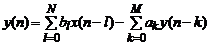
имеют при таком определении вид дробно-рациональной или целой рациональной функций. В результате решение разностного уравнения дискретной системы заменяется более простым решением алгебраических уравнений, описывающих ее передаточную функцию (аналогично операторному методу решения дифференциальных уравнений для аналоговых систем). По известной передаточной функции системы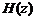 
и 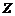-преобразованию входного сигнала 
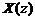путем обратного 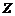-преобразования их произведения можно аналитически найти отклик системы на заданное входное воздействие:
.
Из 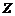-преобразования левых и правых частей ДВС 
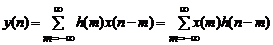получим
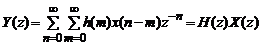
следует, что передаточная функция дискретной системы является 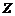-преобразованием ее импульсной характеристики:
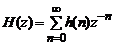. (3.5)
Импульсная характеристика системы соответствует, в свою очередь, обратному 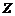-преобразованию ее передаточной функции:
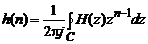. (3.6)
Частотная характеристика дискретной системы, определяемая отношением Фурье-образов выходного и входного сигналов, с учетом связи между 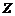- и Фурье-преобразованиями
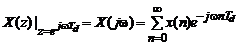(3.7)
находится по передаточной функции системы 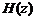простой заменой 
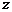на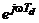 
:
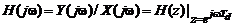. (3.8)
С учетом этой же связи из (3.5) следует, что частотная характеристика дискретной системы, как и аналоговой, является Фурье-преобразованием ее импульсной характеристики:
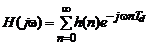, (3.9)
а импульсная характеристика – обратным преобразованием Фурье частотной характеристики:
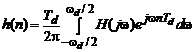. (3.10)
Рассмотрим особенности частотных характеристик дискретных систем.
Легко заметить, что как Фурье-образы дискретных сигналов, так и частотные характеристики дискретной системы (3.8), (3.9) представляют собой функции относительной или нормированной частоты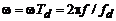 
, называемой также цифровой частотой. Значениям круговой частоты 
в пределах (
) и (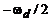
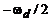) соответствуют значения цифровой частоты 
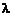в пределах (
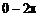) и (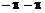
). Частотная характеристика дискретной системы как функция цифровой частоты 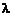определяется выражениями:
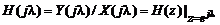; (3.11)
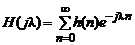. (3.12)
Заданная таким образом частотная характеристика не зависит от значения частоты дискретизации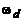 
, а соответствующая ей импульсная характеристика имеет период дискретизации 
.
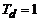Полезно и еще одно возможное представление частотной характеристики в виде отношения мгновенных значений выходного и входного комплексных гармонических сигналов системы в установившемся режиме:
при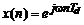 
.
Модуль и аргумент частотной характеристики дискретной системы, представленной в показательной форме: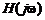 
= = 
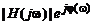, обладают свойством четной и нечетной симметри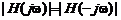и: 
и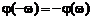 
и называются, соответственно, амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристиками системы. Это же относится и к реальной и мнимой частям комплексной частотной характеристики, первая из которых является четной функцией частоты, а вторая – нечетной.
Из определения частотной характеристики дискретной системы как преобразования Фурье импульсной характеристики (3.9), (3.12) следует также свойство ее периодичности с периодом по частоте 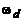или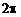 
(рис. 3.2). Оно присуще Фурье-преобразованиям любых дискретных последовательностей. Математически это объясняется периодичностью комплексной экспоненты 
:
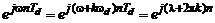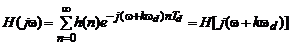
или
,
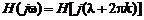где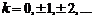 
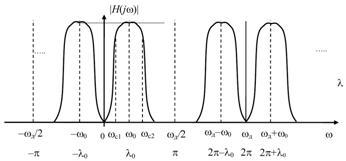
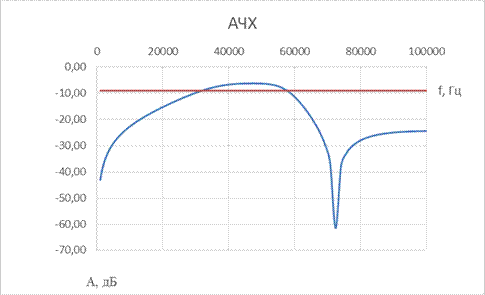
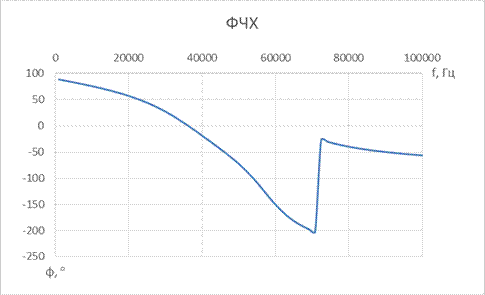
Рис. 3.2. Примерный вид АЧХ цифрового полосового фильтра
При математическом анализе и синтезе цифровых фильтров учитывается один период их частотной характеристики в основной полосе частот от 0 до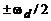 
. Требования к ЦФ и технические описания их характеристик приводятся, как и для аналоговых фильтров, только для реальных положительных частот, в данном случае в диапазоне (
).
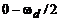Зависимость частотной характеристики ЦФ от частоты дискретизации сигнала, отождествляемой с частотой дискретизации импульсной характеристики фильтра, является еще одной важной для понимания особенностью частотных свойств таких фильтров. Изменение частоты дискретизации с 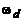на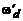 
изменяет масштаб частотной характеристики 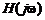по обеим осям в 
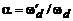раз, пропорционально сжимая или растягивая частотную характеристику ЦФ (это отвечает одному из свойств преобразования Фурье [1]).
Частотной характеристике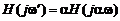 
соответствуют новые значения граничных и центральных частот ЦФ 
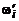, связанные с их исходными значениями 
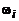(например, 
, 
, 
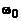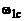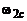на рис. 3.1) соотношением 
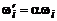. Следовательно, с изменением частоты дискретизации сигнала частотная характеристика ЦФ автоматически перестраивается к новому значению частоты дискретизации.
Как показано выше, от абсолютного значения частоты дискретизации 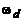не зависит частотная характеристика ЦФ, заданная функцией цифровой частоты : 
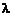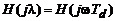. Это означает, что ЦФ с центральной частотой 
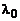частотной характеристики 
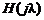будет откликаться на дискретные сигналы с частотами 
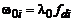, соответствующими различным значениям частот дискретизации 
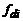этих сигналов.
Таким образом, периодичность, зависимость от частоты дискретизации и конечный верхний предел граничной частоты, равный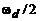 
, принципиально отличают частотные характеристики дискретных систем и цифровых фильтров от аналоговых.
Практическая часть
1. Выберите по два конденсатора и резистора (по возможности разных номиналов) и определите номиналы их значений с помощью платформы NI ELVIS II.
Рассчитайте и постройте графики АЧХ четырехполюсников согласно вашему варианту.
1. ФНЧ Баттерворта 5-го порядка
| № набора | fc, Гц | R = Rн, Ом | C1, мкФ | L1, мкГн | C2, мкФ | L2, мкГн | C3, мкФ |
| 7,5 | 0,68 | 2,2 | 0,68 |
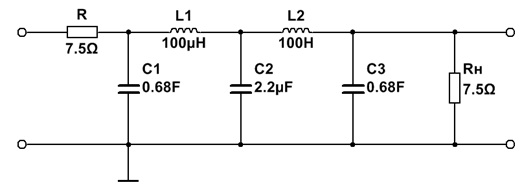
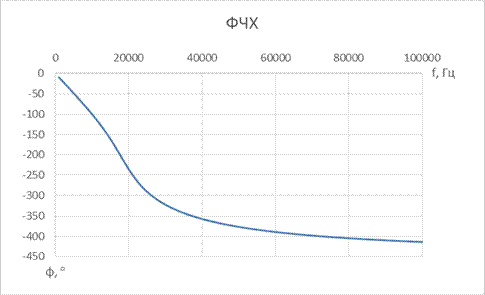
2. ФНЧ Чебышева 5-го порядка
| № набора | fc, Гц | R = Rн, Ом | C1, мкФ | L1, мкГн | C2, мкФ | L2, мкГн | C3, мкФ |
| 2,2 | 3,3 | 2,2 |
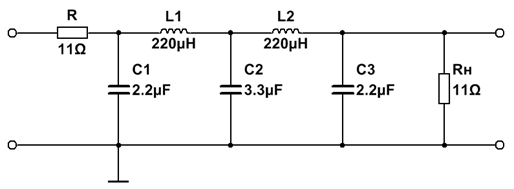
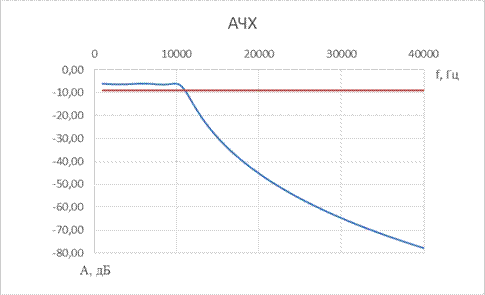
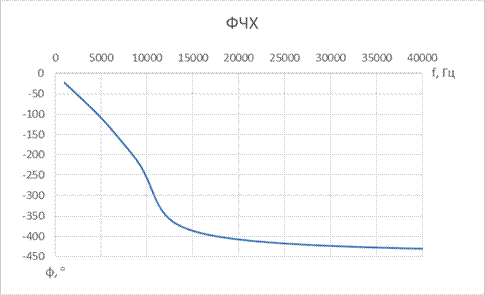
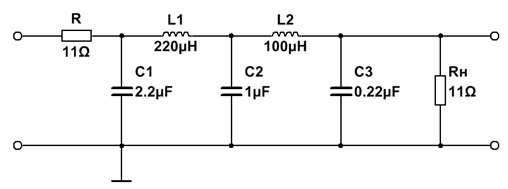
3. ФНЧ Гаусса 5-го порядка
| № набора | fc, Гц | R = Rн, Ом | C1, мкФ | L1, мкГн | C2, мкФ | L2, мкГн | C3, мкФ |
| 2,2 | 0,22 |
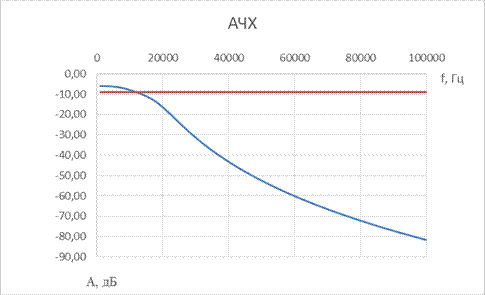
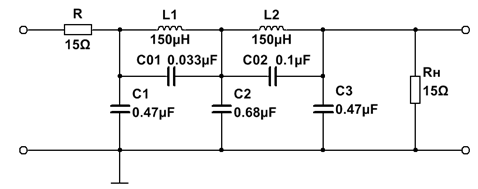
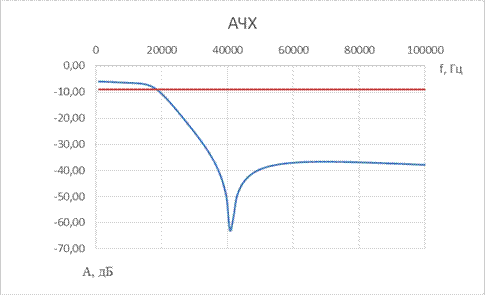
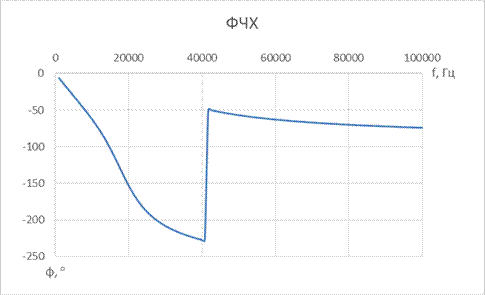
4. ФНЧ Кауэра 5-го порядка
| № набора | fc, Гц | R = Rн, Ом | C1, мкФ | L1, мкГн | C01, мкФ | C2, мкФ | L2, мкГн | C02, мкФ | C3, мкФ |
| 0,47 | 0,033 | 0,68 | 0,1 | 0,47 |
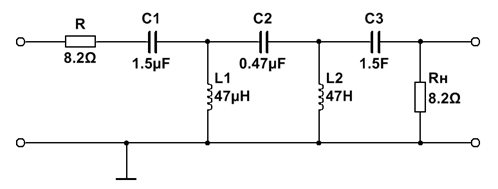
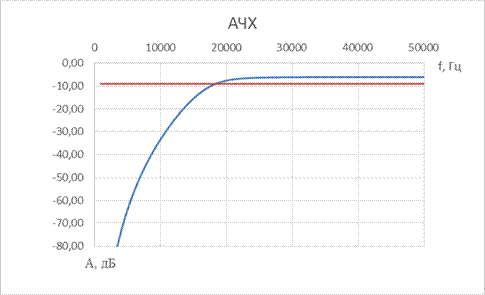
5. ФВЧ Баттерворта 5-го порядка
| № набора | fc, Гц | R = Rн, Ом | C1, мкФ | L1, мкГн | C2, мкФ | L2, мкГн | C3, мкФ |
| 8,2 | 1,5 | 0,47 | 1,5 |
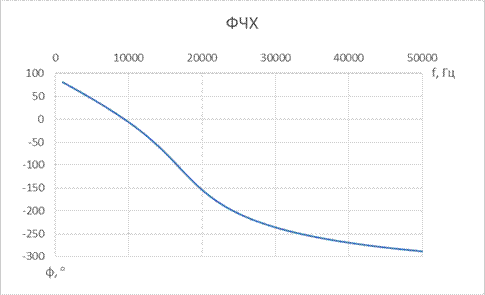
6. ФВЧ Чебышева 5-го порядка
| № набора | fc, Гц | R = Rн, Ом | C1, мкФ | L1, мкГн | C2, мкФ | L2, мкГн | C3, мкФ |
| 7,5 | 0,15 | 0,1 | 0,15 |
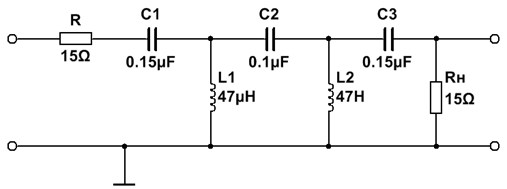
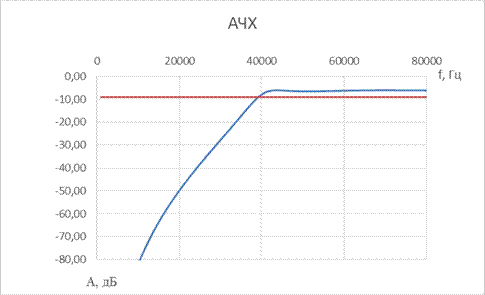
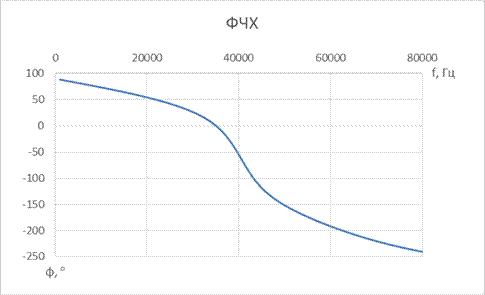
7. ФВЧ Гаусса 5-го порядка
| № набора | fc, Гц | R = Rн, Ом | C1, мкФ | L1, мкГн | C2, мкФ | L2, мкГн | C3, мкФ |
| 8,2 | 2,2 |
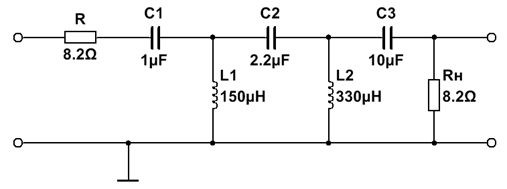
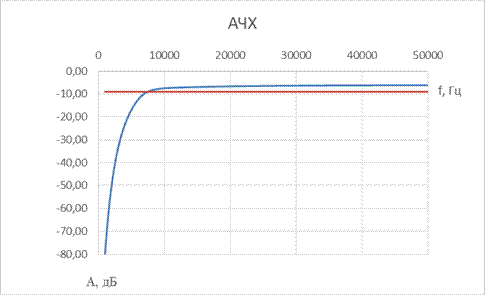
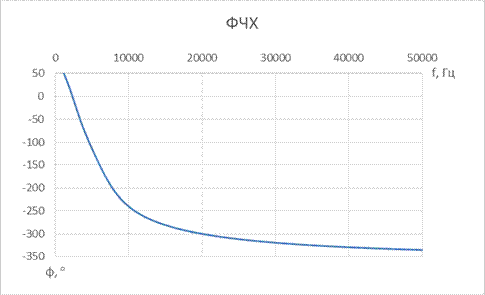
8. ФВЧ Кауэра 5-го порядка
| № набора | fc, Гц | R = Rн, Ом | C1, мкФ | L1, мкГн | C01, мкФ | C2, мкФ | L2, мкГн | C02, мкФ | C3, мкФ |
| 0,15 | 2,2 | 0,1 | 0,22 |
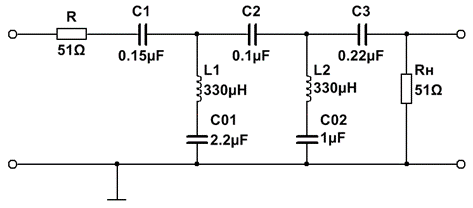
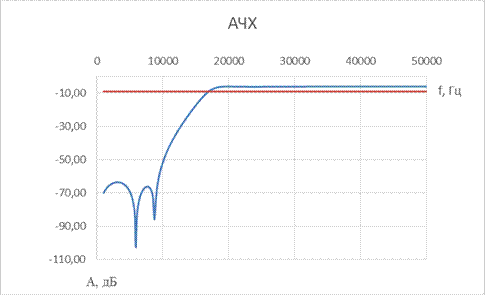
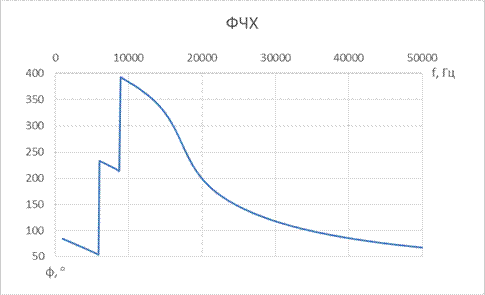
9. ПФ Баттерворта 3-го порядка
| № набора | fcнижн, Гц | fcверх, Гц | R = Rн, Ом | C1, мкФ | L1, мкГн | C2, мкФ | L2, мкГн | C3, мкФ | L3, мкГн |
| 0,22 | 0,68 | 0,22 |
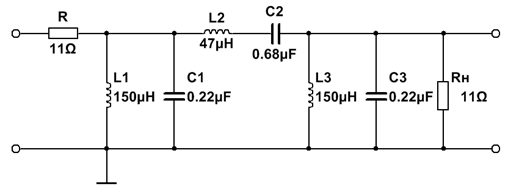
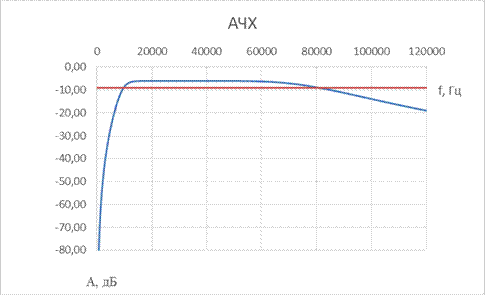
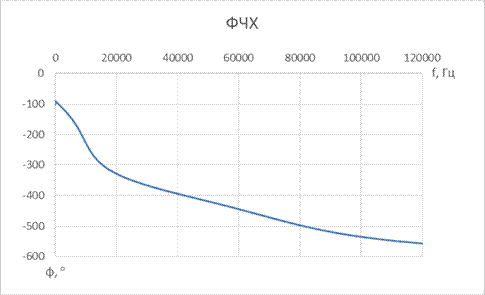
10. ПФ Чебышева 3-го порядка
| № набора | fcнижн, Гц | fcверх, Гц | R = Rн, Ом | C1, мкФ | L1, мкГн | C2, мкФ | L2, мкГн | C3, мкФ | L3, мкГн |
| 0,33 | 0,47 | 0,33 |
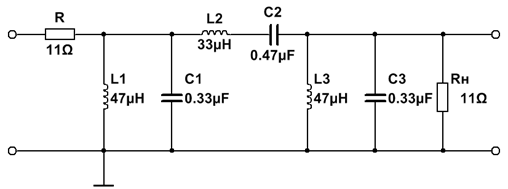
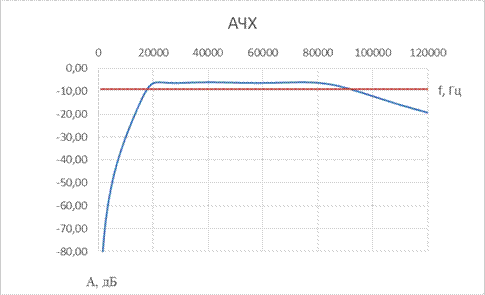
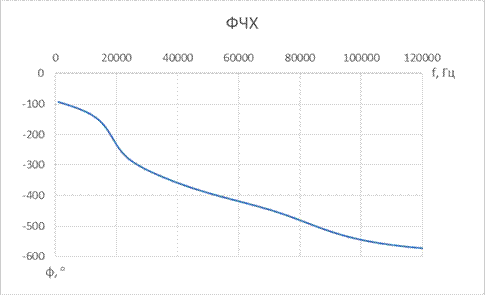
| № набора | fcнижн, Гц | fcверх, Гц | R = Rн, Ом | C1, мкФ | L1, мкГн | C2, мкФ | L2, мкГн | C3, мкФ | L3, мкГн |
| 8,2 | 0,68 | 0,68 | 0,1 |
11. ПФ Гаусса 3-го порядка
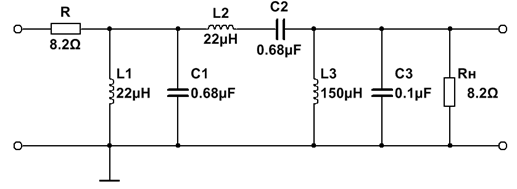
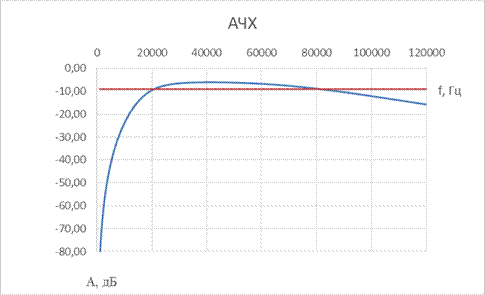
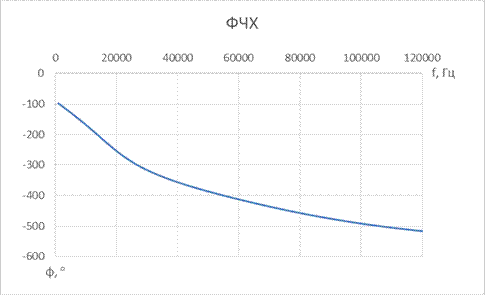
| № набора | fcнижн, Гц | fcверх, Гц | R = Rн, Ом | C1, мкФ | L1, мкГн | C2A, мкФ | L2A, мкГн | C2B, мкФ | L2B, мкГн | C3, мкФ | L3, мкГн |
| 8,2 | 0,47 | 0,015 | 0,22 | 0,47 |
12. ПФ Кауэра 3-го порядка
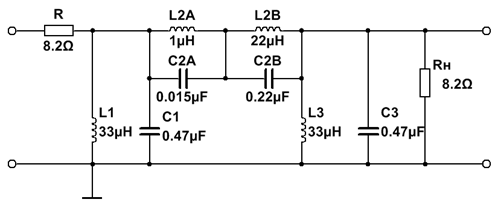
| № вар | № набора | Тип | R = Rн, Ом | fc (fн/fв), Гц | C1, мкФ | L2 (L2A|L2B), мкГн | C3, мкФ | L4, мкГн | C5, мкФ | С02 (C02A|C02B), мкФ | С04, мкФ | L01, мкГн | L03, мкГн | ||
| ФНЧ Баттерворта-5 | 7,5 | 0,68 | 2,2 | 0,68 | - | - | - | - | |||||||
| ФНЧ Чебышева-5 | 2,2 | 3,3 | 2,2 | - | - | - | - | ||||||||
| ФНЧ Гаусса-5 | 2,2 | 0,22 | - | - | - | - | |||||||||
| ФНЧ Кауэра-5 | 0,47 | 0,68 | 0,47 | 0,033 | 0,100 | - | - | ||||||||
| ФВЧ Баттерворта-5 | 8,2 | 1,5 | 0,47 | 1,5 | - | - | - | - | |||||||
| 7,5 | ФВЧ Чебышева-5 | 0,15 | 0,1 | 0,15 | - | - | - | - | |||||||
| ФВЧ Гаусса-5 | 8,2 | 2,2 | - | - | - | - | |||||||||
| ФВЧ Кауэра-5 | 0,15 | 0,1 | 0,22 | 2,20 | 1,00 | - | - | ||||||||
| ПФ Баттерворта-3 | 10000/80000 | 0,22 | 0,22 | - | - | 0,68 | - | ||||||||
| ПФ Чебышева-3 | 20000/80000 | 0,33 | 0,33 | - | - | 0,47 | - | ||||||||
| ПФ Гаусса-3 | 8,2 | 20000/80000 | 0,68 | 0,1 | - | - | 0,68 | - | |||||||
| 8,2 | ПФ Кауэра-3 | 30000/50000 | 0,47 | 1,00 | 22,00 | 0,47 | - | - | 0,015 | 0,22 | - | ||||
2. Разработка ВП для измерения АЧХ четырехполюсника в полуавтоматическом режиме.
2.1. Запустите LabVIEW и создайте новую программу.
Установите на лицевой панели (Front Panel) следующие элементы:
· Numeric Control палитры Modern → Numeric панели элементов Control – это будет поле для ввода частоты генерируемого сигнала,
· Два массива Array (Частоты и Значения КП) из палитры Modern → Array, Matrix & Claster панели элементов Control – для хранения значений частоты и соответствующего ей коэффициента передачи;
· Графический индикатор Ex XY Graph из палитры Graph панели элементов Control – для построения графика АЧХ;
· Две копки OK Button и Stop Button из палитры Modern → Boolean панели элементов Control.
Оформите лицевую панель согласно приведенному рисунку.
2.2. Переключитесь на окно Блок диаграммы (Block Diagram) и установите структуру While Loop из палитры Programming → Structures панели Functions – это будет основной цикл программы. Подключите к терминалу условия продолжения/остановки цикла кнопу Выход
2.3. Внутри цикла While Loop установите структуру Case Structure и подсоедините к его селектору (терминал зеленого цвета) кнопку Выполнить измерение.
2.4. Установите элемент NI ELVISmx Function Generator из палитры Measurement I/O → NI ELVISmx. Подключите к контакту Frequency (Hz) элемент Numeric Control Частота; к контакту Amplitude (Vpp) – константу со значением 5; к контакту Stop – кнопку Выход. Таким образом, генератор будет генерировать синусоиду (это тип сигнала по умолчанию) с амплитудой 5В и частотой указанной в поле Numeric Control Частота до тех пор пока не будет нажата кнопка Выход
2.5. Внутрь Case Structure установите структуру Flat Sequence c 2-мя фреймами.
Внутрь первого фрейма установите элемент NI ELVISmx Oscilloscope. Вызовите контекстное меню на контакте Horizontal выберите Create → Constant отсоедините появившийся кластер-константу от этого контакта. Установите рядом элемент Bundle By Name из палитры Programming → Cluster, Class, &Variant и подсоедините к его верхнему контакту, созданную ранее кластер-константу. Выполните соединение выхода элемента Bundle By Name с контактом Horizontal элемента NI ELVISmx Oscilloscope.
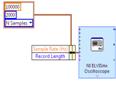
Элемент NI ELVISmx Oscilloscope – по сути является аналого-цифровым преобразователем, основными параметрами которого являются: Частота дискретизации сигнала (Sample Rate (Hz)) и Размер буфера (Record Length) – это размер массива, который будет формироваться при каждом обращении к этому элементу на контакте Cannel 0/1 Out.
Подсоедините к контакту Sample Rate (Hz) значение Частота умноженное на 10 – это означает, что частота дискретизации сигнала будет в 10 раз превышать частоту генерируемой синусоиды.
К контакту Record Length – подсоедините константу 100, т.е. АЦП каждый раз будет выдавать массив по 100 отсчетов или по 10 периодов оцифрованного гармонического колебания.
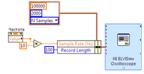
Во-второй фрейм установите элемент Array Max & Min из палитры Programming → Array и подсоединение к его входу выход Cannel 0 Out элемента NI ELVISmx Oscilloscope. Этот элемент необходим для поиска максимума и минимума в массиве данных (оцифрованном сигнале).
Далее выполните соединение согласно рисунку:
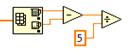
Таким способом определяется амплитуда сигнала:
.
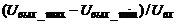На выходе данного фрагмента кода будет формироваться значение коэффициента передачи при заданной частоте сигнала.
2.6. Далее требуется выполнить накопление данных Частоты и Значения КП в соответствующие одномерные массивы. Это реализуется с помощью элементов Initialize Array, Array Size, Insert Into Array и сдвиговых регистров. На основе этих массивов строится график АЧХ – элемент EX XY Graph.
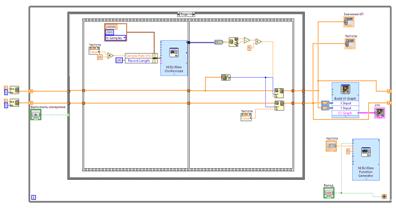
2.7. Соберите на макетной плате RC цепь согласно вашему варианту и выполните следующие соединения:
FGEN → вход RC цепи;
BNC1+ и BNC1- → выход RC цепи;
Ground – земля;
BNC1 → SCOPE CH0.
2.8. Выполните построение АЧХ, задавая значения частоты генератора от 100 Гц до 1000 Гц с шагом 100Гц, далее от 1000 Гц до 10000 Гц с шагом 1000Гц, далее от 10000 Гц до 100000 Гц с шагом 10000 Гц, и от 100000 Гц до 2000000 Гц с шагом 100000Гц.