Сформулируйте и докажите теорему о пределе разности двух бесконечно малых последовательностей.

Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Доказательство:

)

)

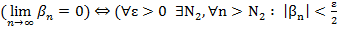Докажем, что .

Если N=max{N₁, N₂}, тогда для N выполняются одновременно неравенства и .

Значит, что

Сформулируйте и докажите теорему об ограниченности бесконечно малой последовательности.

Сформулируйте и докажите теорему о произведении ограниченной последовательности на бесконечно малую последовательность.

Произведение бесконечно малой на ограниченную последовательность есть бесконечно малая последовательность.

Доказательство:

Пусть { x_n } – ограниченная последовательность

{ α_n } – бесконечно малая последовательность

Надо доказать, что

Действительно,

Значит,

2.1.5. Сформулируйте и докажите теорему о пределе последовательности {1/xn}, если последовательность {xn} является бесконечно большой.

Сформулируйте и докажите теорему о единственности предела сходящейся последовательности.

Сформулируйте и докажите теорему об ограниченности сходящейся последовательности.

Сформулируйте и докажите теорему о пределе суммы сходящихся последовательностей.

Сформулируйте и докажите теорему о пределе разности сходящихся последовательностей.

Сформулируйте и докажите теорему о пределе произведения сходящихся последовательностей.

Сформулируйте и докажите теорему о пределе частного сходящихся последовательностей.

Сформулируйте и докажите теорему о предельном переходе в неравенствах.

Сформулируйте и докажите теорему о пределе монотонной последовательности.

2.1.14. Сформулируйте и докажите теорему о монотонности последовательностей {xn}=(1+1/n)n и {xn}=(1+1/n)n+1.

 

Сформулируйте и докажите теорему о существовании предела у монотонной последовательности.

2.1.16. Сформулируйте и докажите теорему о существовании предела последовательности {xn}= (1+1/n)n..

Рассмотрим последовательность {x_n} = {(1+1/n)ⁿ}.

Докажем, что эта последовательность возрастает и ограничена сверху. Применив формулу бинома Ньютона, найдем

Совершенно аналогичным образом запишем элемент

Непосредственным сравнением убеждаемся, что , т.е. последовательность } возрастающая.

Для доказательства ограниченности этой последовательности сверху заметим, что каждое выражение в круглых скобках в соотношении для меньше единицы. Учитывая, что при k≥2 получим:

.

Итак, последовательность {x_n} возрастает и ограничена сверху.

По теореме Вейерштрасса эта последовательность сходящаяся и имеет предел. Этот предел называют числом е.

 

 

Сформулируйте и докажите теорему о существовании предельной точки у ограниченной последовательности.

2.1.18. Сформулируйте и докажите теорему Больцано-Вейерштрасса.

Сформулируйте и докажите теорему о связи существования предела последовательности с равенством верхнего и нижнего пределов этой последовательности.

Сформулируйте критерий Коши для последовательностей.

2.2. Функции