Рассмотрим дискретный СЭ, все «элементарные исходы» которого равновозможны. Соответствующую мат. модель С. Э. называют "классической".
|
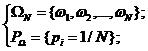
Очевидно, что в рамках классической модели вероятность события 
равна отношению числа благоприятных исходов 
к размерности П.Э.С. NΏ:
Пример. В урне находятся 29 пронумерованных шаров. Найти вероятность того, что номер вынутого НАУГАД шара кратен 3
è 
---------------------------------------------------------------------------------------------------------------
.
Пусть 
- множество "n" различных элементов, из которых составляются различные m –местные комбинации/наборы K(n,m), содержащие “m” элементов:
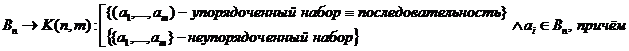
- упорядоченные наборы - последовательности различаются либо порядком, либо составом элементов
n=4,m=3→(b1,b2,b3) (b2,b1,b3) (b4,b1,b3),
- неупорядоченные наборы различаются только составом элементов,включенных в комбинацию:
{b1,b2,b3 } ={b2,b1,b3} ≠ { b4,b1,b3}
. Основное правило комбинаторики: "Если для «построения комбинации» необходимо последовательно выполнить «операции»: 
, причем 
Ai можно выполнить ni способами и после этого Ai+1 можно выполнить ni+1 способами, количество таких различных комбинаций равно 
.
Рассмотрим некоторые m -местные комбинации из n различных элементов.
1. Размещениями из n по m без повторений называются m -местные последовательности
. Так как элемент a1 можно выбрать n1=n способами, после
этого a2 - n2=n-1, …, am - nm=n-m+1 способами, по ОПК количество таких различных комбинаций равно
(1)
2. Перестановками n элементов без повторений называются n -местные последовательности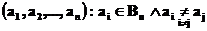 
,различающиеся порядком элементов, т.е. размещения из n по n. Поэтому
NПЕР =P(n)= 
=n! (2)
3. Сочетаниями из n по m без повторений называются неупорядоченные m -местные
комбинации 
.Очевидно, что если в каждом сочетании
выполнить перестановки его m- элементов, получим размещения из n по m. Следовательно
(3)
è Свойства сочетаний: 
Утверждение. n- элементное множество 
имеет 
подмножеств, включая пустое множество и Bn, при этом количество k- элементных подмножеств равно 
.
Пусть и имеется неограниченное количество «копий» каждого элемента.
4. Размещениями из n по m с повторениями называются m -местные последовательности
, элементы которых 
могут повторяться. Так как каждый элемент последовательности ai, i=1,2,…,m можно выбрать ni=n способами, по ОПК количество таких различных комбинаций равно
N = nm (4)
Пример 1. Записать все различные комбинации 1.- 4. для 
Пример 2. Сколькими способами можно разместить 5 различных «шаров» по 8 «бездонным» ящикам?
Сколькими способами можно разместить 5 различных «шаров» по 8 «одноместным» ящикам?
ИДЗ-ТВ1 ПО ТЕМЕ «Непосредственный подсчет вероятностей. Алгебра событий».
Задание.
0) «Известно,что:» - используемые определения и формулы.
Задача 1). Выбрать по условиям задачи ПЭС, построить математическую модель СЭ, определить случайное событие и вычислить его вероятность.
Задача 2). Найти вероятность случайного события, используя «алгебру событий».
Результаты – с 3 в.з.ц.
1. [1] Найти вероятность того, что в лотерее «5 из 49» угаданы хотя бы 4 номера.
(1) Примем за элементарные исходы ω случайного эксперимента сочетания из 49 номеров по 5. 
è Математическая модель случайного эксперимента: 
(2) Случайное событие A={ωA} 
, ωA – такиесочетания из 49 по 5, в которых угаданы
4(А4) или 5(А5) фиксированных чисел, т.е. А = А4+А5.
Так как события А4 и А5 несовместные, P(A)=P(A4)+P(A5).
(3) По основному правилу комбинаторики:
(4) 
--------------------------------------------------------
2. [1] «9 друзей наугад заказали билеты на поезд из 5 вагонов. Найти вероятность того, что друзья оказались в одном или в двух соседних вагонах».
(1) Примем за исходы случайного эксперимента девятиместные комбинацииномеров вагонов, доставшихся 1-му, 2-му, …, 9-му другу, - размещения из 5 по 9 с повторениями è NΩ= 59
(2) Определим случайное событие А как сумму СС: А=А1+А2с ( все попали в какой-либо один или в какие-то два соседние вагона).
Так как СС А1 и А2с несовместные, Р(А)= Р(А1)+Р(А2с).
(3) А1: (выбрать один «общий» вагон) è NА1 =5
А2с: (выбрать два соседних вагона из 5) à (разместить 9 по 2-м выбранным вагонам,
n2c=4 {{1,2}, {2,3}, {3,4}, {4,5} }
исключая 2 варианта: все в одном или все в другом из двух вагонов!!)
n(9,2) = 29-2 è NА2с = n(9,2)∙ n2c =4∙(29-2) è NА =N(A1)+ N(A2с)
(4) Р(А)= 
Результат. А=А1+А2с. Р(А)= Р(А1)+Р(А2с); Р(А)= 
3. [1] «В ящикенаходятся 20 деталей, 5 из которых – стандартные. Найти вероятность того, что из трех взятых наугад деталей по крайней мере одна окажется стандартной».
(1) Примем за пространство элементарных исходов Ω={ω}, ω - сочетания из 20 различных деталей по 3. Размерность N Ω= 
.
(2) Случайное событие А={ ω A}, ω A – такие сочетанияиз 20 по 3, в которых из 3 деталей либо одна, либо две, либо три – стандартные
è Противоположное СС 
такие сочетанияиз 20 по 3, в которых все 3 детали нестандартные.
è Результаты: 
4.[2] Найти вероятность того, что студент сдаст хотя бы два экзамена из трёх, если результаты экзаменов независимы и вероятности сдачи 1,2,3-го экзаменов равны: p1=p3=0.9, р2=0.8.
è 
Результаты: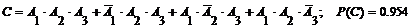 
=======================================================================
Литература.
1)Даугавет А.И., Постников Е.В., Червинская Н.М. Введение в теорию вероятностей.:
Учеб. пособие, СПбГЭТУ «ЛЭТИ» - 2012.
2) Бородин А.Н. Элементарный курс теории вероятностей и математической статистики:
Учеб. пособие для вузов. СПб, Лань,2008.
3) Вентцель Е.С., Овчаров А.А. Теория вероятностей и ее инженерные приложения.
Учеб. пособие для вузов.- М.: Наука, 2000, 2003
4) Вентцель Е.С., Овчаров А.А. Задачи и упражнения по теории вероятностей:
Учеб. пособие для вузов.- М.: Высшая школа, 2002, 2004, 2005.
Самостоятельная работа. Зачет.
ИДЗ-1 “Непосредственный подсчет вероятностей. Алгебра событий»
ИДЗ-2 «Формула полной вероятности. Формула Байеса. Схема Бернулли»
ИДЗ-3 «Дискретная и непрерывная случайная величина».
ИДЗ-4 «Функции случайной величины».