Понятие первообразной функции.
Функция  называется первообразной функцией функции
называется первообразной функцией функции  на интервале
на интервале 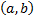 , если всюду на интервале
, если всюду на интервале 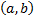 существует производная
существует производная  и эта производная
и эта производная  .
.
Замечание. В определении 1.1 интервал 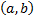 может быть заменён на всю бесконечную прямую
может быть заменён на всю бесконечную прямую  , либо на одну из бесконечных полупрямых
, либо на одну из бесконечных полупрямых 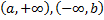 .
.
Примеры: функция  является первообразной функции
является первообразной функции  на интервале
на интервале  , так как всюду на этом интервале
, так как всюду на этом интервале 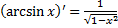 ; функция
; функция 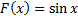 является первообразной функции
является первообразной функции  на бесконечной прямой
на бесконечной прямой  , так как в любой точке этой прямой
, так как в любой точке этой прямой  ; функция
; функция  является первообразной функции
является первообразной функции  на бесконечной полупрямой
на бесконечной полупрямой  , так как
, так как 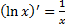 в каждой точке полупрямой
в каждой точке полупрямой  .
.
Если функция  является первообразной функции
является первообразной функции  на интервале
на интервале 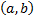 , то функция
, то функция  , где
, где  – произвольная постоянная, также является первообразной функции
– произвольная постоянная, также является первообразной функции  на интервале, так как
на интервале, так как  .
.
Следующая теорема устанавливает связь между различными первообразными одной и той же функции.
Теорема 1.1. Если  и
и  – любые две первообразные функции
– любые две первообразные функции  на интервале
на интервале 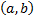 , то всюду на этом интервале
, то всюду на этом интервале 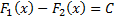 , где
, где  – некоторая постоянная.
– некоторая постоянная.
Доказательство. Обозначим через 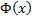 разность функций
разность функций  и
и 
 . Тогда в каждой точке интервала
. Тогда в каждой точке интервала 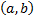 существует
существует  . Из теоремы 1.4 главы 7 следует, что
. Из теоремы 1.4 главы 7 следует, что  . Теорема 1.1 доказана.
. Теорема 1.1 доказана.
Следствие из теоремы 1.1. Если  является одной из первообразных функции
является одной из первообразных функции  на интервале
на интервале 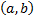 , то любая первообразная
, то любая первообразная 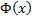 функции
функции  на этом интервале имеет вид
на этом интервале имеет вид 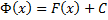 , где
, где  - некоторая постоянная.
- некоторая постоянная.
Неопределённый интеграл.
Совокупность всех первообразных функции  на интервале
на интервале 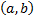 называется неопределённым интегралом и обозначается символом
называется неопределённым интегралом и обозначается символом
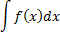
Знак  называется знаком интеграла, выражение
называется знаком интеграла, выражение  - подынтегральным выражением, а сама функция
- подынтегральным выражением, а сама функция  - подынтегральной функцией,
- подынтегральной функцией,  – переменной интегрирования.
– переменной интегрирования.
Из приведенного выше следствия непосредственно вытекает, что если  является одной из первообразных функции
является одной из первообразных функции  на интервале
на интервале 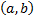 , то
, то

где  - произвольная постоянная.
- произвольная постоянная.
3. Основные свойства неопределённого интеграла.
1.Производная от неопределенного интеграла равна подынтегральной функции

Это равенство непосредственно вытекает из равенства (1):

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению
 .
.
Действительно, если  одна из первообразных функции
одна из первообразных функции  , то
, то
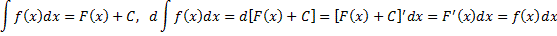
3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной
 .
.
В самом деле, так как  то
то  .
.
Следующие два свойства называются линейными свойствами неопределенного интеграла.
4. Постоянный множитель можно выносить из-под знака интеграла, т.е.

где 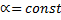 .
.
Действительно, если  первообразная функции
первообразная функции  , то
, то  – первообразная функции
– первообразная функции  , так как
, так как  . Из чего следует, что
. Из чего следует, что 
 , где
, где  .
.
5. Неопределённый интеграл от суммы или разности двух функций равен соответственно сумме или разности неопределённых интегралов этих функций, т.е.

Действительно, пусть  и
и  первообразные функций
первообразные функций  и
и 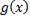 соответственно:
соответственно:

Так как  , то функция
, то функция  является первообразной функции
является первообразной функции  .
.

 , где
, где 
 Следовательно
Следовательно 
4. Таблица основных интегралов.
Приведённые ниже интегралы принято называть табличными интегралами.
1. 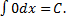
2.  .
.
3. 
4. 
5. 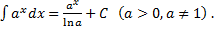
6. 
7. 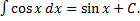
8.  .
.
9. 
10. 
11. 
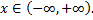
12.  .
.
13. 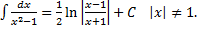
Справедливость всех приведённых формул, за исключением формул 4, 12, 13, непосредственно следует из определения неопределённого интеграла и таблицы производных элементарных функций. Сделаем замечания в отношении формул 4, 12 и 13. Формула 4 справедлива для любого интервала, не содержащего точки  . Действительно, если
. Действительно, если  то из равенства
то из равенства 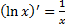 заключаем, что
заключаем, что  , а если
, а если  , то из равенства
, то из равенства  заключаем, что
заключаем, что  . Следовательно, формула 4 справедлива для любого
. Следовательно, формула 4 справедлива для любого  .
.
Докажем равенство 12.
Рассмотрим функцию  Очевидно, в каждой точке бесконечной прямой
Очевидно, в каждой точке бесконечной прямой  ,
, 
 Поэтому
Поэтому
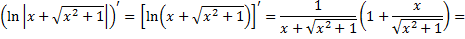
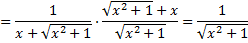
Следовательно

Рассмотрим теперь функцию  . Данная функция определена на множестве
. Данная функция определена на множестве  . Если
. Если 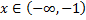 то
то  , поэтому для любой точки полупрямой
, поэтому для любой точки полупрямой 


Следовательно, на полупрямой  справедливо равенство
справедливо равенство

Очевидно, на полупрямой 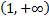 ,
,  . Поэтому
. Поэтому

Т.е. и на полупрямой 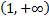 , справедливо равенство
, справедливо равенство

Справедливость равенства (13) проверить самостоятельно.