Задание цифровых автоматов на начальных языках
Рассмотрим начальные языки, наиболее часто используемые для описания функционирования ЦА: язык граф схем алгоритмов (ГСА) и язык логических схем алгоритмов (ЛСА).
Граф-схемы алгоритмов
Язык ГСА является простейшим и самым распространённым языком, применяемым для описания функционирования управляющих микропрограммных устройств. Это объясняется их наглядностью, простотой конструкции, а также простотой преобразований и формального перехода к таблицам перехода и аналитическому представлению алгоритмов в виде систем канонических уравнений (СКУ).
Язык ГСА – графический язык, поэтому символы, применяемые в нём, имеют определённое геометрическое начертание, определяемое ГОСТом. ГСА – ориентированный связный граф, содержащий одну начальную (A 0), одну конечную (Ak) и произвольное конечное множество условных X ={ x 1,..., xL } и операторных A ={ A 1,..., AM } вершин (рис. 3.4).
Рис. 3.4. Вершины ГСА
Любой алгоритм должен начинаться и заканчиваться символами начальной и конечной вершин. Начальная вершина A 0 не имеет входов, конечная вершина не имеет выходов. Конечная, операторная и условная вершины имеют по одному входу, причём входящая линия может быть образована слиянием нескольких линий. Начальная и операторная вершины имеют по одному выходу, а условная – два выхода, помеченных символами 1 и 0. Операторной вершине сопоставляется вполне определённый оператор Ai, символизирующий некоторые действия
Y ={ y 1, y 2,..., yN }. Разрешается в различных операторных вершинах запись одинаковых элементов множества Y. Внутри условных вершин записывается логическое условие, принимающее значение 1 или 0. Разрешается в различных условных вершинах запись одинаковых элементов множества X ={ x 1, x 2,..., xL }.
ГСА удовлетворяет следующим условиям:
1. Входы и выходы вершин соединяются друг с другом с помощью дуг, направленных от выхода к входу.
2. Каждый выход соединён точно с одним входом.
3. Любой вход соединяется, по крайней мере, с одним выходом.
4. Для любой вершины графа существует, по крайней мере, один путь из этой вершины к конечной вершине.
5. Один из выходов условной вершины может соединяться с её входом, что не допустимо для операторной вершины.
При соединении выхода условной вершины с её входом в цепь обратной связи вводится пустая операторная вершина, отмеченная пустым выходным сигналом ye. (рис. 3.5, а).
Пустые операторные вершины ставят на выходе условной вершины в начале цикла. Возможно неверное изображение (рис. 3.5, б).
Рис. 3.5. Ввод пустой операторной вершины
При разработке алгоритма работы ОУ вначале записывается содержательная ГСА, в которой внутри операторных и условных вершин записывается содержательное обозначение микроопераций и логических условий. Например,
При кодировании содержательной ГСА внутри операторных вершин записываются символы из множества выходных сигналов
Y = { y 1, y 2,..., yN }., а внутри условных вершин символы из множества входных сигналов X = { x 1, x 2,..., xL }.. Например:
Рассмотрим выполнение алгоритма по ГСА (рис.3.6).
Выполнение алгоритма начинается с оператора A 0. На следующих двух шагах выполняются операторы A 1 и A 2. На четвёртом шаге может выполняться один из трёх операторов A 3, A 4 и Ak или пустой оператор
Ae в зависимости от значений логических условий x 1, x 2 и x 3. Если
x 1= x 2 = 0, то независимо от значения сигнала x 3будет выполняться пустой оператор Ae, т.е. автомат будет находиться в режиме ожидания, выдавать пустой сигнал ye до тех пор, пока x 1или x 2не станут равными единице. Если 
= x 2=1, то выполняется оператор A 3; если
x 1 = 1, то выполняется A 4, при x 3 = 1 или Ak при x 3= 0.
Рис. 3.6. Пример ГСА
Предположим, что после выполнения A 2 имеет место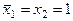 
. Тогда независимо от значения x 3, будут последовательно выполняться A 2 и A 3 до тех пор, пока после очередного выполнения оператора A 2 и проверки логических условий, логическое условие x 1 не станет равным единице. После этого выполняется оператор A 4 или Ak, как было отмечено выше. Выполнение алгоритма закончится оператором Ak.
Шаг алгоритма – это путь на ГСА от одной операторной вершины к другой, состоящий только из условных вершин.
Построение таблиц переходов по ГСА
Алгоритм построения таблицы переходов для автомата Мура будет включать следующие этапы:
1) Пронумеровать все операторные вершины ГСА, предварительно введя пустые операторные вершины, если в ГСА имеются циклы из условных вершин.
2) Каждому оператору ГСА поставить в соответствие вполне определенное состояние автомата, присвоив ему индекс, соответствующий номеру вершины ГСА. Причем одинаковым операторам, стоящим в разных местах ГСА, должны соответствовать разные состояния. Это обеспечивается сквозной нумерацией вершин ГСА. Начальной вершине будет соответствовать исходное состояние автомата. Часто начальную и конечную вершины ГСА совмещают, тогда автомат после выполнения алгоритма переходит в начальное состояние.
3) Осуществить просмотр всех путей перехода, ведущих от одной операторной вершины к другой, начиная с исходного состояния. Причем, каждый такой путь должен соответствовать шагу алгоритма и состоять только из логических условий (условных вершин). Оператор, стоящий вначале пути, должен соответствовать состоянию автомата в момент времени t, а в конце пути – в момент времени (t +1);
Каждому пути из логических условий от одного оператора к другому сопоставить конъюнкцию входных сигналов. Причем в конъюнкцию входной сигнал xi войдет без отрицания, если выход из условной вершины отмечен единицей, и с отрицанием, если нулем.
4) Построить таблицу переходов автомата Мура. Для этого необходимо анализировать все полученные пути между операторными вершинами, учитывая, что каждая операторная вершина отмечена совокупностью выходных сигналов.
Пример 3.1. Построить прямую таблицу переходов и СКУ по ГСА, показанной на рис. 3.6, для автомата Мура.
Решение. Введя сквозную нумерацию операторных вершин и следуя предложенному алгоритму, получим прямую таблицу переходов автомата Мура (табл. 3.1). По табл. 3.1 запишем СКУ и СВФ.
| Таблица 3.1 Таблица переходов автомата Мура | СКУ:
a 1(t +1) = a 0;
a 2(t+ 1) = a 1  a 4;
a 3(t+ 1) = a 2  1 2 a 3 1 2;
a 4(t+ 1) = a 2 1 x 2 a 3 1 x 2;
a 5(t+ 1) = a 2 x 1 x 3 a 3 x 1 x 3;
a 6(t+ 1) = a 2 x 1 3 a 3 x 1 3 a 5.
СВФ: y 0= a 0;
y 1 = a 1 a 5;
y2 = a 2 a 5;
y 3 = a 4;
ye = a 3;
yk = a 6.
| |||
| ai(t) | yi(t) | xij(t) | aj (t+ 1) | |
| a 0 | y 0 | a 1 | ||
| a 1 | y 1 | a 2 | ||
| a 2 | y2 | x 1 x 3
x 1 3
1 x 2
1 2
| a 5 a 6 a 4 a 3 | |
| a 3 | ye | x 1 x 3
x 1 3
1 x 2
1 2
| a 5 a 6 a 4 a 3 | |
| a 4 | y 3 | a 2 | ||
| a 5 | y 1, y 2 | a 6 |
В том случае, если требуется построить прямую таблицу переходов для автомата Мили, необходимо в таблице переходов автомата Мура объединить те состояния, при переходе из которых под действием одинаковых входных сигналом совпадают не только выходные сигналы, но и состояния автомата, то есть состояния, переходы из которых полностью совпадают.
Примечание. При построениипрямой таблицу переходов для автомата Мили необходимо в таблице переходов автомата Мура выходной сигнал yj (t +1) приписывается состоянию автомата aj (t+ 1).
Пример 3.2. Построить прямую таблицу переходов и СКУ по ГСА, показанной на рис. 3.6, для автомата Мили.
Решение. Полученную ранее прямую таблицу переходов автомата Мура (табл. 3.1) можно использовать для эквивалентного ему автомата Мили можно использовать, если отметить состояния автомата aj (t+ 1) соответствующими выходными сигналами yi (t +1). Получим табл. 3.2. Анализ табл. 3.2 показывает, что переходы из состояний a 2 и a 3 и состояний a 1 и a 4 полностью совпадают. Объединим соответствующие этим состояниям строки и введем следующие обозначения состояний минимального автомата Мили:
a 0 = a 0; a 1 a 4 = a 1; a 2 a 3 = a 2 ; a 5 = a 3; a 6 = a 4.
Подставим введенные обозначения в табл. 3.2 получим таблицу переходов автомата Мили (табл. 3.3).
| Таблица 3.2 Таблица переходов автомата Мили | Таблица 3.3 Минимальная таблица переходов автомата Мили | |||||||
| ai(t) | xj(t) | aj (t+ 1) | yij (t) | ai(t) | xij(t) | aj (t+ 1) | yj(t+1) | |
| a 0 | a 1 | y 1 | a 0 | a 1 | y 1 | |||
| a 1 | a 2 | y 2 | a 1 | a 2 | y 2 | |||
| a 2 | x 1 x 3
x 1 3
1 x 2
1 2
| a 5 a 6 a 4 a 3 | y 1, y 2 yk y 3 ye | a 2 | x 1 x 3
x 1 3
1 x 2
1 2
| a 3 a 4 a 1 a 2 | y 1, y 2 yk y 3 ye | |
| a 3 | x 1 x 3
x 1 3
1 x 2
1 2
| a 5 a 6 a 4 a 3 | y 1, y 2 yk y 3 ye | a 3 | a 4 | yk | ||
| a 4 | a 2 | y2 | ||||||
| a 5 | a 6 | yk |
По табл. 3.3 запишем СКУ и СВФ для автомата Мили:
| СКУ: | a 1(t +1) = a 0  a 2  1 x 2;
a 2(t+ 1) = a 1 a 2 1 2;
a 3(t+ 1) = a 2 x 1 x 3;
a 4(t+ 1) = a 2 x 1 3 a 3.
| СВФ: | y 1 = a 0 a 2 x 1 x 3;
y 2 = a 1 a 2 x 1 x 3;
y 3 = a 2 1 x 2;
yk = a 2 x 1 3 a 3.
|