
υ* U (S) δв (S) ω Z (S) υ (S)
υ (S) ω Z (S)
Рисунок 6.
«Структурная схема АС, отвечающая преобразованной математической модели».
Произведём преобразование полученной ранее передаточной функции (1.6).
 (1.8)
(1.8)
 -коэффициент усиления ЛА
-коэффициент усиления ЛА
(1.9)
 - постоянная времени;
- постоянная времени;
(1.10)
 - коэффициент демфирования;
- коэффициент демфирования;
(1.11)
 (1.12)
(1.12)
Подставив (1.9),(1.10),(1.11),(1.12) в формулу (1.8) получим
 (1.13)
(1.13)
Найдём передаточную функцию разомкнутой системы, т.е. исходную систему необходимо привести к виду, показанному на рисунке 7

Рисунок 7.
Для того чтобы перейти к данной модели необходимо сделать ряд преобразований (рис.8, 9).

Рисунок 8.
 ; (1.14)
; (1.14)

Рисунок 9.
 ; (1.15)
; (1.15)


(1.16)
 , где
, где 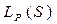 - многочлен числителя,
- многочлен числителя,  - многочлен знаменателя,
- многочлен знаменателя,
 ,
,
 ,
,

 . (1.17)
. (1.17)
Найдем передаточную функцию замкнутой системы, тем самым преобразуем АС вида, указанного на рисунке 7, к следующему виду (рис. 10):

Рисунок 10.
 (1.18)
(1.18)

где  ,
,
 ,
,
 , (1.20)
, (1.20)
 ,
,
 .
.
Построение частотных характеристик АС
Определение корней характеристического уравнения разомкнутой системы
Используя математический пакет программ, вычислим корни характеристического уравнения вида:  .
.
 (1.21)
(1.21)
Разложим многочлен знаменателя передаточной функции разомкнутой системы на множители.

(1.22)
Передаточная функция в виде произведения элементарных звеньев
Передаточную функцию (1.22) можно представить в виде элементарных звеньев.
 - пропорциональное звено (коэффициент усиления разомкнутой системы). (1.23)
- пропорциональное звено (коэффициент усиления разомкнутой системы). (1.23)
 - форсирующее звено 1 порядка. (1.24)
- форсирующее звено 1 порядка. (1.24)
 - интегрирующее звено
- интегрирующее звено
 - апериодическое звено 1 порядка, где
- апериодическое звено 1 порядка, где
 (1.25)
(1.25)
 - апериодическое звено 1 порядка, где
- апериодическое звено 1 порядка, где
 . (1.26)
. (1.26)
Определим частоту среза для каждого звена
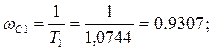
 (1.27)
(1.27)
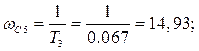
Определим Краз
 (1.28).
(1.28).
Построение ЛАЧХ, ЛФЧХ и АФЧХ
Используя пакет программ SIAM, построим ЛАЧХ, ЛФЧХ (рис.11) и АФЧХ (рис. 12).
Рисунок 11.
«ЛАЧХ,ЛФЧХ»
Рисунок 12.
«АФЧХ»
Построим ЛАЧХ и ЛФЧХ, используя аналитический метод, все расчёты представлены в таблице 2 и таблице 3.
Таблица2
«ЛАЧХ»
| ω | 0,01 | 0,1 | 0,930752 | 1,3036 | 14,97886 | ||||
| 20lgA1ω | 8,048798 | 8,048798 | 8,048798 | 8,048798 | 8,048798 | 8,048798 | 8,048798 | 8,048798 | 8,048798 |
| 20lgA2ω | 0,000501293 | 0,04984501 | 3,0103 | 3,333133 | 4,715332 | 20,66078 | 24,14963 | 40,6237 | 60,62332 |
| 20lgA3ω | 0,62332 | -2,30289 | -20 | -23,5096 | -40 | -60 | |||
| 20lgA4ω | -1,93565E-06 | -0,0001936 | -0,01674 | -0,01931 | -0,03277 | -1,60078 | -3,0103 | -16,5868 | -36,4914 |
| 20lgA5ω | -5,42568E-06 | -0,0005425 | -0,04675 | -0,05392 | -0,09124 | -3,52049 | -5,8013 | -21,0013 | -40,9671 |
| lgω | -2 | -1 | -0,03117 | 0,115144 | 1,175479 | ||||
| СумLg | 48,04929 | 28,0979 | 11,6184 | 11,30844 | 10,3369 | 3,5878 | -0,1232 | -28,9161 | -68,7868 |
Таблица3
«ЛФЧХ»
| ω | 0,01 | 0,1 | 0,930752 | 1,303600 | 10,000000 | 14,97886 | |||
| φ1 | |||||||||
| φ2 | 0,61556217 | 6,13233485 | 47,05408 | 54,4737 | 84,6825 | 86,44434 | 89,46673 | 89,94667 | |
| φ3 | -0,439511013 | -4,3866054 | -35,5263 | -37,492 | -45 | -82,5728 | -85,0261 | -89,2531 | -89,9253 |
| φ4 | -90 | -90 | -90 | -90 | -90 | -90 | -90 | -90 | -90 |
| φ5 | -0,074594832 | -0,7459395 | -6,93576 | -7,4506 | -9,70452 | -66,9379 | -90 | -163,363 | -178,326 |
| lgω | -2 | -1 | -0,03117 | 0,115144 | 1,175479 | ||||
| Сумф | -89,89854368 | -89,00021 | -87,4621 | -87,8886 | -90,2308 | -154,828 | -178,582 | -253,15 | -268,305 |
где  - амплитудная функция,
- амплитудная функция,
 - фазовая функция
- фазовая функция
 ;
;  ;
;
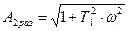 ;
;  ;
;
 ;
;  ; (1.29)
; (1.29)
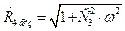 ;
;  ;
;
 ;
;  .
.
По этим вычислениям построим ЛАЧХ и ЛФЧХ (рис.13,14).

Рисунок 13.

Рисунок 14.
Исследование устойчивости АС
Анализ устойчивости с помощью критерия Гурвица
Запишем характеристический многочлен замкнутой системы, т.е. знаменатель передаточной функции замкнутой системы.
 . (2.1)
. (2.1)
По критерию Гурвица для устойчивости линейной системы необходимо и достаточно, чтобы при  все главные определители матрицы Гурвица были положительными.
все главные определители матрицы Гурвица были положительными.
Запишем матрицу Гурвица.
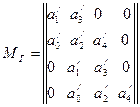 . (2.2)
. (2.2)
Для нашего случая достаточно, чтобы  или
или  .
.
 , (2.3)
, (2.3)
 ,
,
 по критерию Гурвица замкнутая система устойчива.
по критерию Гурвица замкнутая система устойчива.
Определение критического коэффициента усиления разомкнутой системы по критерию Гурвица
Для нашего случая имеем  .
.
Критическим коэффициентом усиления разомкнутой системы называется то значение, при котором замкнутая система выходит на границу устойчивости.
Следовательно, передаточная функция разомкнутой системы будет:
 .
.
Характеристический многочлен замкнутой системы будет функцией двух переменных
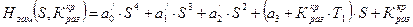 . (2.4)
. (2.4)
Чтобы найти 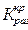 решим уравнение
решим уравнение 
 ,
,
 ,
,
 ,
,

 ,
,
 ,
,
 .
.