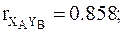В методе наименьших квадратов доказывается, что обратные веса уравненных неизвестных
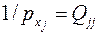(3.41)
где Qjj - так называемые весовые коэффициенты. Они являются диагональными элементами матрицы
(3.42)
получаемой обращением матрицы R, т. е. Q = R-1. Так как RQ = E то, обозначив j-й столбец матрицы Q через Qj, а матрицы Ε – череp Ej, получим k систем нормальных уравнений вида
(3.43)
Как видно, системы (3.43) и (3.19) имеют одну и ту же матрицу коэффициентов R. Отсюда следует, что для вычисления элементов столбцов Qj матрицы Q в схему Гаусса необходимо дополнительно ввести столбцы – Еj, равные
, 
, 
и, рассматривая их как новые столбцы свободных членов, по каждому из них получить k столбцов Qj. Более того, если каждый из столбцов – Ej условно обозначить как столбец свободных членов
то элементы столбцов Qj получим по тем же формулам, что и.неизвестные δxj.
Так, в задаче 3.17 вычисление величин Qjj приведем в табл. 44.
Контролем вычислений являются равенства Qij = Qji, так как матрица Q, как и R, симметричная. Обычно при вычислениях табл. 43 и 44 совмещают, помещая столбцы - Ej вслед за столбцом «контроль» в табл. 43, а элементы Qij, ниже строки «контроль» в левой нижней части этой таблицы.
| Таблица 44 | |||||
| δx1 | δx2 | δx3 | -Ε1 | -Ε2 | -Ε3 |
| 3,00 -1,00 | 2,00 -0,667 | 1,00 -0,333 | - 1 0,333 | ||
| 2,67 - 1,000 | 1,33 -0,498 | 0,67 -0,251 | -1,00 0,374 | ||
| 2,00 - 1,000 | 0,50 -0,250 | - 1,00 0,500 |
Приведем дополнительно способ вычисления любого элемента матрицы Q, не требующего знания остальных ее элементов. Он основан на следующих соображениях.
Матрицу коэффициентов нормальных уравнений всегда можно представить в виде произведения двух треугольных матриц Т1 и Т2
составленных из элементов элиминационных строк, взятых с обратным знаком, и эквивалентных строк схемы Гаусса. Собственно на этом представлении и основан способ Гаусса. Так как RQ = Е, то полуаем T1T2Q = Ε, откуда следует
Можно показать, что элементы матриц Τ-11 и Т-12 как раз и содержатся в столбцах Εj таблиц: в нечетных строках с обратным знаком элементы матрицы Τ-11, а в четных - элементы матрицы (Τ-12)Т .Так, в нашем примере
Перемножив эти матрицы, получим матрицу Q. Но вычисления удобно выполнять в таблице вида табл. 44 по следующему правилу: любой элемент Qij матрицы Q равен взятой с обратным знаком сумме произведений чисел всех элиминационных строк из столбца – Εi на элементы эквивалентных строк из столбца – Ej (так называемый способ диагоналей). Например, Q11 = - (0,333-0,67 X 0,251) = 0,500, Q22 = (0,374 - 0,250 Χ 0,50) = 0,500, Qi2 = - 0,251 и т. д. Средние квадратические ошибки уравненных неизвестных вычисляют по формуле 
где для равноточных измерений· средняя квадратическая ошибка одного измерения вычисляется по формуле 
(обобщение формулы Бесселя, получаемой при k = 1). Так, в задаче 3.17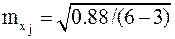 
= 0,54" и
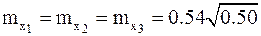= 0,38"
матрицу M2 = m2Q называют корреляционной матрицей уравненных неизвестных (см. § 22).
Заметим, что 
есть коэффициенты корреляции между уравненными i-м и j-м неизвестными. Так, коэффициент корреляции между первым и вторым углом
Способ Ганзена вычисления весовых коэффициентов. Рассмотренный выше способ вычисления весовых коэффициентов называют способом дополнительных столбцов. В этом способе вычисляют все величины Qjj, Однако объем вычислений можно сократить, если воспользоваться свойством симметричности матрицы Q. В самом деле, приняв для простоты k= 3, напишем три системы эквивалентных уравнений, соответствующих системе нормальных уравнений (3.43). Будем иметь
(3.44)
(3.45)
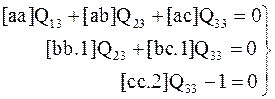(3.46)
Здесь знаком вопроса заменены свободные члены этих уравнений, вычислить которые не придется. Далее из последнего уравнения системы (3.46) сразу находим
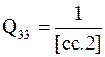(3.46’)
из второго уравнения
и, наконец,
Таким образом, для вычисления столбца
вводить дополнительный столбец свободных членов и не требуется (величина 
уже содержится в схеме Гаусса как вспомогательная величина, остальные же числа элиминационных строк этого столбца равны нулю).
Поскольку Q32 = Q23, то последнее уравнение в системе (3.45) для определения Q32 не потребуется. Приняв в качестве Q32 величину Q23, из второго уравнения (3.45) находим
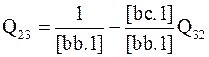
а из первого уравнения
Замечаем, что величина 
уже имеется в схеме Гаусса, а элемент первой элиминационной строки в дополнительном столбце свободных членов равен нулю. Так что и для получения столбца Q2, как и столбца Q3, также не нужно вводить дополнительный столбец. Рассуждая аналогичным образом и переходя к системе (3.44), находим
приняв Qn = Q21, Ql3 = Q31.
Ясно, что и в этом случае нет необходимости вводить дополнительный столбец свободных членов.
Вычисления целесообразно располагать по следующей схеме (на примере задачи 3.17).
| (0,3333) | 3,00 (-1,000) | 2,00 -0,667 | 1,00 -0,333 | |
| (0,3745) | 2,67 (-1,000) | 1,33 -0,498 | ||
| (0,5000) Контроль | 2,00 (-1,000) | |||
| 1,000 | 0,500 | -0,250 | ||
| 0,998 | -0,250 | 0,499 | -0,249 | = Q |
| 1,002 | -0,249 | 0,500 |
В ней вычисления начинают с последней строки (в которой размещают элементы столбца Q3), как описано выше. В дальнейшем все вычисляемые величины заносят в нижнюю часть этой схемы, выделенную жирной ломаной линией. В верхнюю же часть заносят числа из нижней по мере продвижения по строкам вверх. Так, вычислив элементы третьей строки, число -0,249 переносят во вторую строку, а вычислив элементы второй строки, начиная с 0,499, в первую строку переносят элементы -0,250 из второй строки и из третьей. В первой строке вычислений находится лишь элемент Q1 = 0,500.
Следует, однако, иметь в виду, что при вычислении Qijэтим способом ошибки, которые могут быть допущены, не обнаруживаются и вся матрица Q может быть получена неверной. Поэтому каждый столбец Qjначиная с последнего, следует контролировать дополнительно. Необходимые для этого равенства вытекают непосредственно из формулы (3.43) и имеют вид
Полученные правые части этих равенств целесообразно записать в специальном столбце «Контроль» (см. схему). Расхождения здесь допустимы до 0,002-0,003 (при вычислении элементов матрицы Q - до 0,001).
Хотя этот способ изложен нами для k = 3, его несложно обобщить и на любое число k. Заметим также, что оба рассмотренных способа применяют для обращения симметричных матриц как вручную, так и на ЭВМ и называют способом Гаусса.
Из формул (3.41) и (3.46') следует сразу, что вес последнего неизвестного рx3 =[cc.2] или в общем случае
(3.46")
Нетрудно получить также формулу для вычисления веса предпоследнего неизвестного
(3.47)
или в общем случае
(3.48)
Так, в нашем примере рХ3 = 2,00.
Алгоритмы Гаусса
Поэтому
Так как веса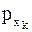 
и 
легко вычислить, то последними в геодезической сети обычно нумеруют те пункты, которые предполагают наименее точными из всех (расположенные в самом слабом месте).
3.18. Решить по способу Гаусса, применяя сокращенную схему, одну из следующих систем нормальных уравнений:
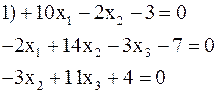
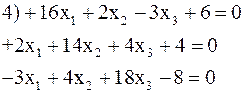
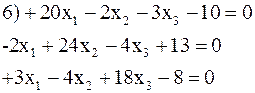
Ответы:
1) 0,402; 0,509; —0,225.
2) —0,408; 0,107; —0,314.
3) —0,557; 0,648; —0,404.
4) 0,356; 0,318; 0,314.
5) 2,468; 3,552; 1,915.
6) 0,413; —0,462; 0,272.
7) —0,834; 0,927; —0,779.
8) —0,559; 0,583; —0,705.
9) 0,209; —0,506; —0,470.
10) —0,013; 0,050; 0,028.
3.19. Обратить по способу Ганзена матрицу коэффициентов одной из систем нормальных уравнений, приведенных в задаче 3.18.
3.20.Является ли нормальной матрица
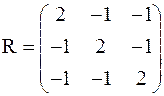
Указание! Вычислить ее определитель согласно формуле (3.28).
Ответ: нет.
3.21. Будет ли являться нормальной матрица R = ATA, если матрица
3.22. Составить уравнение поправок, нормальное уравнение и оценить точность уравненного неизвестного в общем виде для случая n-кратного измерения одной и той же величины. Доказать, что x= [х]/n, рх = n, а также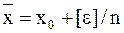 
(см. § 21).
3.23. Дана матрица весовых коэффициентов уравненных координат xAyA, xByB,
Найти все шесть коэффициентов корреляции между уравненными координатами.
Ответ: 
