С применением метода наименьших квадратов тесно связан вопрос о так называемом сглаживании экспериментальных зависимостей. Пусть производится опыт, целью которого является исследование зависимости некоторой физической величины Υ от физической величины X, причем предполагается, что Υ и X связаны функциональной зависимостью Υ = φ(Χ).
В результате наблюдений получены пары чисел
(xiyi) (i = 1, 2,..·, n).
О форме зависимости судят, исходя из существа задачи, или по внешнему виду экспериментальной зависимости. Например, экспериментальные точки, изображенные на рис. 53, предполагают прямолинейную зависимость вида у = ах + b, а на рис. 54 - полином второй степени у = ах2 + bх + с. В общем случае можно говорить
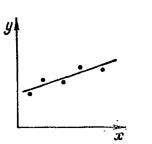
Рис. 53
Рис. 54
Рис. 55
о подборе полинома степени n-1, который задает кривую, проходящую через все n точек (хi yi). Но построение такого полинома нецелесообразно, ибо существующая закономерность будет искажена случайными ошибками наблюдений. Для сглаживания случайных уклонений как раз и служит метод наименьших квадратов.
С его помощью определяют параметры а, b, с сглаживающих полиномов. Так, для прямолинейных зависимостей будем иметь уравнения (3.3) вида
………………..
(n>2)
Здесь роль неизвестных играют два параметра а и b, а роль измерений li - величины у; коэффициенты при а и b образуют матрицы
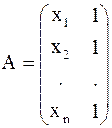
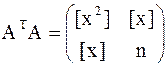
Поэтому имеем систему нормальных уравнений с двумя неизвестными
Решение легко выполнить с помощью обратной матрицы
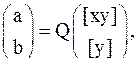
где
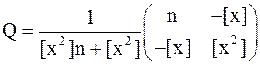
Отсюда
(3.66)
(3.67)
| Таблица 77 | |||
| Номера наблю дений | xi | yi | υi |
| 2,8 | -0,16 | ||
| 2,7 | +0,11 | ||
| 2,9 | +0,08 | ||
| 3,3 | -0,16 | ||
| 3,2 | +0,11 | ||
| 3,4 | +0,08 | ||
| 3,6 | +0,05 | ||
| 3,9 | -0,08 | ||
| 4,0 | -0,02 | ||
| 4,2 | -0,04 | ||
| Σ | 34,0 | -0,03 |
Рассмотрим пример. Пусть имеем пары наблюдений (xiyi), представленные в табл. 77 и на графике в виде точек (рис. 55).
Далее вычисляем:
[x2] = 385, [ху] = 200,9, [x2]n – [x2] = 325.
График показывает, что можно предположить функциональную зависимость у = ах + b. Согласно формулам (3.66) и (3.67) имеем
Далее вычисляем уклонения (см. табл. 77) υi=0.168xi+b-уi, и осуществляем контроль на основании (3.15) или в подробной записи [xυ] = -0,18 = 0; [υ] =-0,03 = 0.
Для оценки точности вычисляем
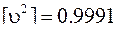
Согласно формуле (3.47) 
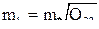где
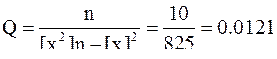
Поэтому
Можно показать, что когда функциональная зависимость имеет вид y=ax+b, задача нахождения параметров a и b математически тождественна задаче построения уравнения регрессии, однако по существу отличается от неё, так как наличие функциональной связи предполагает, что коэффициент корреляции r = 1. Так применяя метод наименьших квадратов к задаче 2.41 получим то же уравнение регрессии y=0.63x+0.71, но говорить о функциональной связи y и x не приходится(это видно по расположению точек на графике рис. 33).
Аналогично решается задача и для подбора параметров полиномов более высокого порядка в общем виде.
3.42 Составить коэффициенты нормальных уравнений для определения коэффициентов полинома y=ax2+bх + с.
| Таблица 78 | |||||
| Номера наблюдений | xi | yi | Номера наблюдений | xi | yi |
| 1,0 | 2,2 | 7,1 | 54,9 | ||
| 2,1 | 6,0 | 7,8 | 71,0 | ||
| 3,1 | 12,4 | 9,0 | 91,0 | ||
| 3,9 | 19,2 | 10,3 | 107,8 | ||
| 5,0 | 31,0 | 10,8 | 129,7 | ||
| 6,2 | 40,8 | 12,0 | 158,3 |
3.43. Определить коэффициенты сглаживающего полинома у=ах2+bх + с по следующим результатам измерений (табл. 78) и оценить их точность.
Рассмотрим здесь еще одну специальную задачу применения параметрического способа уравнивания. Пусть выполнено n измерений одной и той же величины и получены результаты yi искаженные систематическими ошибками ic, где с = const. Требуется из результатов измерений вывести не только уравненное значение величины X, но и оценить систематическую ошибку. В этом случае уравнения поправок будут υi=δx+ic+li где li = х(0)— уi. В качестве приближенного значения можно принять х(0)= 0 или какое-то удобное для вычисления значение, близкое к yi. Так как матрица коэффициентов уравнений поправок имеет вид
то получим матрицу коэффициентов нормальных уравнений
Вектор свободных членов будет
Решение получим с помощью обратной матрицы
(3.68)
по формуле
(3.69)
| Τаблица 79 | |||||
| Номера приемов | Значения уi | Номера приемов | Значения yi | Номера приемов | Значения Уi |
| 90°15'27,5" 29,7 | 90°15'37,3" 33,6 | 90°15'35,5" 38,8 | |||
| 29,7 30,9 | 31,7 33,2 | 33,3 32,1 | |||
| 34,6 | 37,9 | 38,7 | |||
| 34,1 | 34,9 | 39 1 | |||
| 31,3 | 35,3 | 39,4 | |||
| 33,5 | 27,2 | 39,9 |
Средние квадратические ошибки
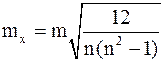
Где
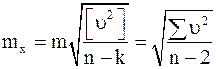(3.70)
Рассмотрим следующий пример. В табл. 79 даны 24 измерения зенитного расстояния на одном из пунктов триангуляции*.
Предполагая, что измерения выполнялись равномерно во времени и влияние систематической ошибки пропорционально времени, получить наиболее надежное значение измеренного угла, оценку систематической ошибки с и оценить точность измерений и результатов.
Решение. В качестве приближенного значения х(0) примем величину х(0)=90°15'20". Тогда найдем
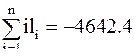
Матрица (3.68)
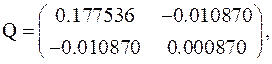
поэтому решение (3.69)
По смыслу задачи это будет наиболее надежное значение угла, отнесенного к начальному моменту измерений.
Для величины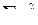 
опуская здесь вычисления, согласно формуле (3.70) найдем
Поэтому точность измерений характеризуется средней квадратической ошибкой
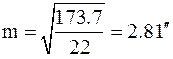
а ошибки
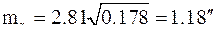
Заметим, что если решать эту задачу, не предполагая наличия систематических ошибок, то получим
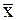= 90°15'34,3"
и m = 3,72", не соответствующую точности измерений данным теодолитом.
3.44. Доказать, что если в каждом измерении одной и той же величины систематическая ошибка постоянна, то ее невозможно выявить рассмотренным способом, а величина m не будет искажена систематическим влиянием.
3.45. Составить матрицу коэффициентов нормальных уравнений, если систематическая ошибка действует по законам: 1) (i + b)с, 2) i2с, 3) аi2с, приняв n= 5.
3.46. С помощью таблицы случайных чисел (прил. XI) смоделировать ошибки n = 10 измерений со стандартом σ = 2 и с = 1, если систематические ошибки действуют по закону ic, где i - номер измерения. Получить оценку для систематической ошибки, оценить точность ее определения и точность измерений.
3.47. Сделать то же самое, если закон действия систематических ошибок φ(с) = c sin αj, где αj = αj-1 + 1°
§ 34. УРАВНИВАНИЕ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ ПАРАМЕТРИЧЕСКИМ СПОСОБОМ
Уравнивание неравноточных измерений выполняется под условием [ρυυ]= VTPV = min, где pi - веса измерений, а Р - диагональная матрица,
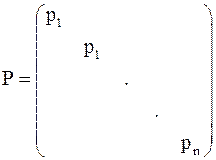
Вопрос установления весов pi был нами рассмотрен в § 24. Исходная система связи и уравнения поправок составляются так же, как и в случае равноточных измерений, но в отличие от него система нормальных уравнений имеет вид
(3.71)
где алгоритмы
…………………………………….
………………………………….
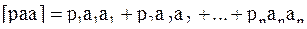
В матричной форме уравнения (3.71) можно записать в виде
(3.72)
где
(3.73)
(3.74)
Процесс вычислений при уравнивании неравноточных измерений, следовательно, отличается от уже рассмотренного случая лишь схемой составления нормальных уравнений. При этом можно поступить двояко: 1) привести неравноточные измерения к равноточным путем умножения i-го уравнения поправок на величину 
2) нормальные уравнения составлять непосредственно по формулам (3.13) и (3.14).
В первой схеме (А) будем иметь систему уравнений поправок
…………………………………..
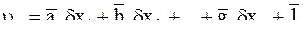
Где
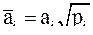
и систему нормальных уравнений
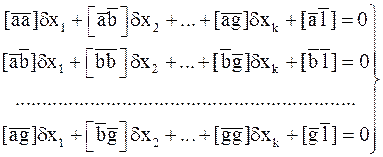
совпадающую с (3.72). Ясно, также, что [ρυυ] = [ 
]. Схема составления системы нормальных уравнений будет состоять из следующих двух таблиц (табл. 80, 81). Для простоты принято k = 3.
Во второй схеме (В), которую применяют чаще, приходится составлять следующие таблицы (табл. 82 и 83).
| Таблица 80 | ||||||
| Номера измерении | ai bi ci li | si | 
| 
| 
| 
|
| 1 2 | a1 b1 c1 l1 a2 b2 c2 l2 ………… an bn cn ln | s1 s2 … s3 | 
…
| 
……..
| 
…
| 
… 
|
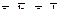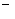
| Таблица 81 | |||
| |||
| 
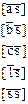
| Контроль | |
| Таблица 83 | |
|
| |
| Контроль |
| Таблица 82 | ||||||
| Номера измерений | ai bi ci li | si | pi | ai pi bi pi ci pi li pi | sipi | υi |
| … n | a1 b1 c1 l1 a2 b2 c2 l2 …………….. an bn cn ln | s1 s2 … sn | p1 p2 …. pn | a1 p1 b1 p1 c1 p1 l1 p1 a2 p2 b2 p2 c2 p2 l2 p2 ………………………………….. an pn bn pn cn pn ln pn | s1p1 snp2 … snpn | υ1 υ2 … υn |
Решение нормальных уравнений, оценка точности неизвестных и их функций выполняется точно так же, как и в случае равноточных измерений. Следует лишь иметь в виду, что во всех формулах, относящихся к этому процессу, в алгоритмах Гаусса с двумя буквами добавляется буква р.
3.48. Уравнять параметрическим способом нивелирную сеть, представленную на рис. 56 (исходные данные приведены ниже), а результаты измерений - в табл. 84.
| Таблица 84 | |||
| Номера ходов | Превышение hi, м | Длина хода Li, км |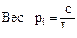 
|
| +6,135 | 33,0 | 1,21 | |
| +8,343 | 33,9 | 1,17 | |
| +5,614 | 30,4 | 1,31 | |
| + 1,394 | 32,7 | 1,22 | |
| -6,969 | 31,8 | 1,25 | |
| -0,930 | 29,9 | 1,34 | |
| +6,078 | 34,5 | 1,15 |
Марки Высоты исходных
марок, м
А 183,506
В 192,353
С 191,880
Рис. 56
Решение. Приближенные значения высот реперов получаем так:
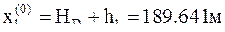
Составляем уравнения поправок:
| Таблица 85 | |||||||
| Номера уравнений | |||||||
| + 1 | 0,0 | + 1,0 | 1,21 | -2,64 | |||
| - 1 | + 1 | - 1,7 | - 1,7 | 1,17 | +0,08 | ||
| + 1 | 0,0 | + 1,0 | 1,31 | -0,85 | |||
| -1 - | + 1 | -8,5 | -8,5 | 1,22 | -2,69 | ||
| - 1 | + 1 | -4,8 | -4,8 | 1,25 | -0,77 | ||
| + 1 | 0,0 | + 1,0 | 1,34 | +3,17 | |||
| + 1 | +0,9 | + 1,9 | 1,15 | +0,05 | |||
| - 1 | +2 | +3 | -14,1 | - 10,1 | |||
| δxj Контроль | -2,64 0,00 | -0,85 0,01 | +3,17 -0,01 | [ρυυ] = 32,42 |
| Таблица 86 | |||||||||
| a] | b] | с] | l] | s] | Контроль | F1 | F2 | Σ | SQ |
| [pa +3,60 [pb [pc [pl [ps | - 1,17 +4,88 | -1,22 -1,25 +3,81 | +12,36 +5,05 -16,37 + 121,9 | + 13,57 +7,51 -15,03 + 122,30 +128,35 | + 13,57 7,51 - 15,03 122,30 128,35 | + 1,00 | 1,00 -1,00 | +2,21 +3,46 +0,34 1,00 | 12,97 6,61 -16,03 |
| Σ1=[as]-[al]+(f1)1+(f1)2 Σ2=[bs]-[bl]+(f2)1+(f2)2 Σ3=[cs]-[cl]+(f3)1+(f3)2 |
Свободные члены выражены в сантиметрах.
Веса измерений вычисляем по формуле pi= 40/Li.
В табл. 85 и 86 приведены коэффициенты уравнений поправок и нормальных уравнений.
В качестве оцениваемых функций выбраны превышения по ходам 1 и 5. Для первой функции F1 коэффициенты f1 = 1, f2 = 0, f3 = 0, для второй f1 = 0, f2 = 1, f3 = - 1. В столбце Σ табл. 86 два последних числа равны соответственно [f]1 = 1 и [f]2 = 0.
Решение системы нормальных уравнении приведено в табл. 87.
В результате проведенного решения получены следующие значения неизвестных:
X1 = 189,641 м - 2,64 см = 189,615 м;
Х2= 197,967 м - 0,85 см = 197,953 м;
х3= 190,950 м + 3,17 см = 190,981 м.
Средние квадратические ошибки единицы веса и на 1 км хода равны:
Вес последнего неизвестного равен
Вес первого неизвестного получен дважды
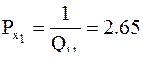
Вес предпоследнего неизвестного
Средние квадратические ошибки:
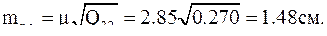
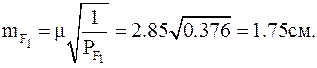
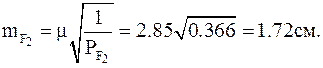
После введения поправок в измеренные величины получим
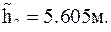
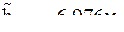
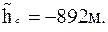
| Таблица 87 | ||||||||||||||
| δx1 | δx2 | δx3 | l | S | Контроль 1 | Q1 | Q2 | Q3 | Qs | Контроль 2 | F1 | F2 | Σ | Контроль 3 |
| +3,60 (0,2778) (-1) | - 1,17 +0,325 | -1,22 +0,339 | + 12,36 -3,433 | + 13,57 -3,769 | + 13,57 -3,769 | - 1,00 +0,278 | +12,57 -3,492 | 12,57 -3,491 | + 1,00 -0,278 | +2,21 -0,614 | +2,21 -0,614 | |||
| (0,2222) | 4,50 (-1) | -1,65 +0,366 | +9,071 +2,015 | 11,92 -2,649 | + 11,92 -2,649 | -0,32 +0,072 | - 1,00 +0,222 | + 10,60 -2,355 | + 10,60 -2,355 | +0,32 -0,072 | + 1,00 -0,222 | +4,18 -0,929 | +4,17 -0,928 | |
| (0,3571) | +2,80 | -8,86 +3,171 | -6,07 +2,172 | -6,06 +2,171 | -0,46 +0,164 | -0,37 +0,131 | - 1,06 +0,357 | -7,89 +2,818 | -7,90 +2,823 | +0,46 -0,164 | -0,63 +0,227 | +2,62 -0,936 | +2,63 -0,937 | |
| 32,44 | 32,44 32,44 |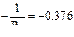 
| +0,031 -0,366 | -0,345 -0,333 | -0,345 -0,335 | |||||||||
| δx1 | δx2 | δx3 | ||||||||||||
| -2,636 -3,638 | -0,855 - 1,855 | +3,171 +2,171 | ||||||||||||
| + 1,002 | 1,000 | 1,000 | ||||||||||||
| Весовые коэффициенты | ||||||||||||||
| +0,376 +0,132 +0,164 | +0,132 +0,270 +0,131 | +0,164 +0,131 +0,358 |
Окончательным контролем правильности решения задачи является выполнение равенства 
для каждого хода сети.
Способ узлов проф. В. В. Попова для составления нормальных уравнений
Для случая уравнивания нивелирных сетей и углов в сети полигонометрии проф. В. В. Попов предложил следующие правила составления нормальных уравнений с помощью чертежа сети:
а) квадратичные коэффициенты нормальных уравнений в строке j равны сумме весов ходов, сходящихся в узле с тем же номером j;
б) неквадратичные коэффициенты, расположенные в строке i и столбце h, равны отрицательному весу хода, соединяющего узлы с номерами j и h;
в) свободные члены нормальных уравнений получаются суммированием величин ±Pili тех ходов, которые сходятся в узле j, причем если узел является конечной точкой хода, то ставится знак «+», а если начальной, то «-».
Например, для нивелирной сети (см. рис. 56) нормальные уравнения будут
а свободные члены
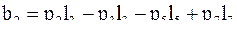
Указанные правила тождественны следующим формулам составления матрицы R системы нормальных уравнений (3.72) ее диагональные элементы
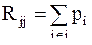(3.75)
(запись i 
j означает здесь принадлежность i-го хода j-му узлу), а недиагональные
(3.76)
(знак суммы предусматривает случай, когда узлы j и k соединены несколькими ходами).
Вектор свободных членов b имеет элементы
(3.77)
3.49. Составить по способу В. В. Попова систему нормальных уравнений в задаче 3.48.
3.50. Выполнить параметрическим способом уравнивание сети триангуляции (рис. 57), если. в ней измерены дирекционные углы
Рис. 57
Номера дирекционных Измеренные значения
углов
1 229°30'17,9'
2 294 06 17.4
3 183 34 12,7
4 238 54 00,7
5 281 56 01,2,
матрица весов которых
Координаты исходных пунктов взять из задачи 3.36. Исходные дирекционные углы
αOA =0°; αOB = 135°40’19,5".
Приближенные значения координат определяемых пунктов примем равными приведенным ниже:
Пункт Ρ x(0) y(0)
D 623,360 - 1393,272
С - 897,701 - 1488,183
Решение. Эта задача отличается от решенной ранее задачи 3.37 лишь тем, что теперь дирекционные углы неравноточны**. Таблицы коэффициентов уравнений поправок и составления нормальных уравнений имеют вид, приведенный в табл. 88, 89.
Решение нормальных уравнений и получение матрицы весовых коэффициентов представлено в табл. 90, а вычисление поправок 
, 
с контролем 
и 
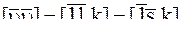- в табл. 88.
Уравненные значения координат и уравненных дирекционных углов приведены ниже.
Пункт F х(р) у(0)
D 623,376 -1393,264
С -897,721 1488,173
Номера дирекционных углов Уравненные дирекционные
1 229°30'18,6"
2 294 06 17,2
3 183 34 13,3
4 238 54 00,2
5 281 56 02,6
При уравнивании этого построения имеем всего одно избыточное измерение, поэтому вычислить ошибку единицы веса μ не представляется возможным. Однако учитывая, что в качестве измеренных углов здесь приняты предварительно уравненные углы из задачи 3.36, можно применить формулу
где через 
- обозначены поправки углов, уравненных в задаче 3.36.
| Таблица 88 | ||||||||||||||||
| ai | bi | ci | di | li | si | 
| 
| 
| 
| 
| 
| 
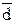
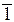
| Контроль |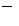 
| 
| |
| 0,858 | -0,731 | -0,1 | 0,027 | 1,414 | 1,213 | -1,034 | -0,141 | 0,038 | 0,038 | 1,01 | 0,71 | |||||
| 1,234 | 0,552 | -2,7 | -0,914 | 2,000 | 2,468 | 1,104 | -5,400 | -a, 828 | -1,828 | -0,46 | -0,23 | |||||
| -0,084 | 1,350 | 0,084 | - 1,350 | 1,1 | 1,100 | 1,414 | -0,119 | 1,909 | 0,119 | -1,909 | 1,556 | 1..556 | 1,556 | 0,81 | 0,57 | |
| 1,018 | -0,614 | 2,2 | 2,604 | 2,000 | 2,038 | -1,228 | 4,400 | 5,208 | 5,210 | -0,95 | -0,48 | |||||
| 0,662 | 0,140 | 2,6 | 3,402 | 1,414 | 0,936 | 0,198 | 3,676 | 4,810 | 4,808 | 1,96 | 1,39 | |||||
| 
Коэффициенты увеличены в 10 раз
|
| ||||||||||||||
| Таблица 89 | |||||||
|
|
|
|
|
|
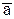
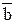
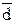
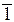
| Контроль | |
| 7,577 | 1,243 | -0,014 | 0,227 | - 13,683 | -4,650 | -4,650 |
| 5,932 | 0,227 | -3,644 | 0,913 | 0,913 | ||
| 5,043 | -2,544 | 12,593 | 15,301 | 15,305 | ||
| 5,191 | -7,646 | -8,414 | -8,416 | |||
| 64,474 | 52,884 | 52,893 | ||||
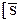
| 56,024 | 56,034 |
| Таблица 90 | |||||||
| Вспомогательные величины | 
| 
| 
| 
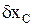
| l | s | Контроль |
| (0,1320) | 7,577 (-1) | 1,243 -0,1640 | -0,014 0,0018 | 0,227 -0,0300 | -13,683 1,8056 | -4,650 0,6137 | -4,650 0,6134 |
| (0,1746) | 5,728 -1 | ■0,229 -0,0400 | -3,681 0,6426 | -0,601 0,1049 | 1,676 -0,2926 | 1,675 -0,2925 | |
| (0,1986) | 5,034 -1 | -2,296 0,4760 | 12,592 -2,5014 | 15,230 -3,0254 | 15,230 -3,0254 | ||
| (0,5965) | 1,678 (-1) | -1,628 0,9713 | 0,048 -0,0286 | 0,048 -0,0287 | |||
| 1,6398 0,6401 | 0,8106 -0,1894 | -2,0391 -3,0390 | 0,9713 -0,0286 | 6,626 | 6,623 6,611 | |
| 0,9997 | 1,0000 | 0,9999 | 0,9999 | 10-4 | |||
| 1,000 1,000 0,999 1,001 | 0,1470 - 0,0776 -0,0356 -0,0784 | -0,0776 0,4069 0,1691 0,3720 | -0,0356 0,1691 0,3337 0,2839 | -0,0784 0,3720 0,2839 0,5965 |
Тогда
Оценка точности уравненных координат выполняется по формулам
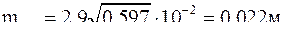
а их функций - точно так же, как и в задачах 3.36-3.38, а именно:
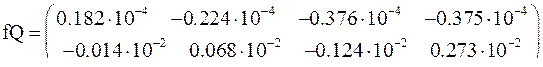
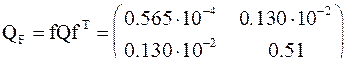
Поэтому
3.J51. Для условий задачи 3.50 составить нормальные уравнения, пользуясь схемой А (не приводя измерения к равноточным). Сделать выводы о преимуществе схемы А или В с точки зрения объема и точности вычислений.
Рис. 58
3.52. Выполнить уравнивание нивелирной сети, изображенной на рис. 58. Оценить точность всех узловых реперов (матрицу весовых коэффициентов
получить по способу Ганзена) и уравненного превышения hi. Обратный вес этой функции вычислить по формуле (3.49) и в дополнительном столбце схемы Гаусса. Исходные данные приведены ниже, а измеренные превышения и длины ходов даны в табл. 91. Нормальные уравнения составить дважды: по схеме В и по способу узлов проф. В. В. Попова.
Номера опорных реперов Высоты опорных реперов, м
I 188,452
II 188,838
III 186,298
3.53. Выполнить предварительное уравнивание углов в полигонометрической сети (рис. 59). Оценить точность дирекционных углов узловых направлений, совпадающих со сторонами 1-30 и 2232. Суммы измеренных левых углов в ходах и исходные дирекционные углы на рис. 59 [3].
Решение. Суммы измеренных углов в каждом ходе принимаем в качестве измеренных величин (как и превышения ходов в нивелирной сети). Веса ходов принимаем равными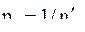 
, где 
- число измеренных углов в каждом ходе. Предполагается, что на узловых точках углы измерены отдельно друг от друга. Далее вычисляем приближенные значения дирекционных углов сторон 1-30 и 2-32 по ходам 1 и 3:
= 196°08'42,3', 
= 162°38'47,1".
| Таблица 91 | |||||||||||
| Превышения, м | Длина хода, км | ||||||||||
| Варианты | |||||||||||
| +2,214+0,001i | 12,8 | 13,4 | 14,0 | 8,0 | 11,1 | 11,8 | 13,2 | 15,1 | 16,6 | 17,5 | |
| +1,566 | 14,2 | 14,8 | 15,5 | 8,9 | 12,3 | 13,1 | 14,6 | 16,7 | 18,3 | 19,4 | |
| -0,302 | 8,7 | 9,1 | 9,5 | 5,4 | 7,6 | 8,0 | 8,9 | 10,2 | 11,2 | 11,8 | |
| -1,881 | 12,4 | 13,0 | 13,6 | 7,7 | 10,7 | 10,4 | 12,8 | 14,6 | 16,0 | 16,9 | |
| +0,915 | 5,8 | 6,1 | 6,4 | 3,6 | 5,1 | 5,4 | 6,0 | 6,9 | 7,5 | 7,9 | |
| -2,814 | 5,1 | 5,3 | 5,6 | 3,2 | 4,4 | 4,8 | 5,2 | 6,0 | 6,5 | 6,9 | |
| -3,137 | 7,8 | 8,3 | 8,6 | 4,9 | 6,8 | 7,2 | 8,1 | 9,2 | 10,1 | 10s6 | |
| + 1,517+0,001i | 10,1 | 10,7 | 11,1 | 6,3 | 8,8 | 9,4 | 10,4 | 12,0 | 13,1 | 13,8 |
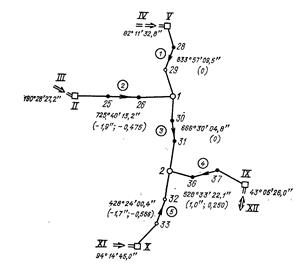
Рис. 59
Свободные члены уравнений поправок (фактически это невязки ходов, взятые с обратным знаком) вычисляем по формуле
где k - такое число, при котором выполняется неравенство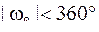 
Ясно что по ходам 1 и 3 невязки равны 0. Нормальные уравнения составляем по способу узлов проф. В. В. Попова по формулам (3.75), (3.76) и (3.77) без составления уравнения поправок, так как коэффициенты перед неизвестными δα1 и δα2 как и в нивелирных сетях, равны ± 1 или 0. В общем виде нормальные уравнения будут
где свободные члены
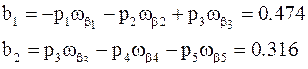
Величины 
и 
приведены в скобках на рис. 59. В результате вычислений получаем систему
Решая ее путем обращения матрицы, находим
Далее для углов каждого хода вычисляем величины
(
)
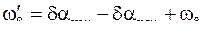
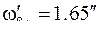
представляющие собой поправки в суммы углов ходов. Контроль вычислений вытекает из формулы [paυ] = [pbυ] =... = 0 и приобретает вид
Соответственно для узлов 1 я 2 получаем
1) 0,207 - 0,268 + 0,060 = - 0,001,
2)- 0,060 + 0,411 - 0,351 = 0.
Поправки в углы в каждом ходе вычисляем по формуле
(здесь они не приводятся).
Далее по известным формулам вычисляем дирекционные углы всех сторон. Для оценки точности вычислим величину
Средняя квадратическая ошибка измерения одного угла
а ошибка 
уравненных дирекционных углов
Коэффициент корреляции между ними 
Если на узлах углы измерены способом круговых приемов, то им следует приписать вес, равный 2, а всем остальным углам - веса, равные 1. Тогда вес суммы углов хода с одним узлом найдем, исходя из формулы
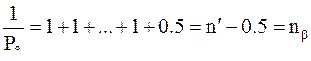
и вес
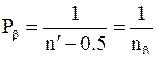
где, как и ранее, n' - число вершин хода, включая узловую точку. Для хода
Рис. 60
«от узла к узлу» 
. Все вычисления аналогичны выполненным ранее стой разницей, что поправки углов на узловых точках вычисляются по формуле