Если предел функции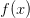 
при 
равняется 
, то найдётся окрестность точки 
, во всех точках которой функция 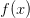ограничена.
Доказательство:
Из определения предела по Коши получим: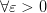 
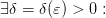
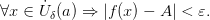Возьмём 
. Из условия теоремы следует существование окрестности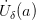 
. Следовательно, 
. Перепишем это следующим образом: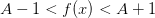 
. Легко видеть, что это и означает ограниченность функции .
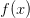31.
32. Теорема о непрерывности функции в точке, свойства непрерывных функций:
Функция 
называется непрерывной в точке 
, если:
функция определена в точке и ее окрестности;
существует конечный предел функции в точке ;
это предел равен значению функции в точке , т.е.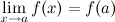 
Свойства:
1. Если функция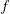 
непрерывна в точке , то она ограниченна в некоторой окрестности этой точки:
2. Если функция 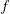непрерывна в точке и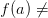 
0, то в некоторой окрестности точки знак функции совпадает со знаком числа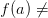
3. Если 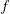и 
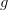непрерывны в точке , то функции:
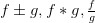непрерывны в точке .
4. Если 
непрерывна в точке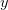 
, а 
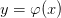, непрерывна в точке 
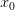причем 
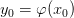, то в некоторой окрестности 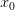определена сложная функция равная 
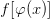которая также непрерывна в точке :
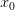33. Точки разрыва и их классификация:
Точка , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:
функция определена в точке и ее окрестности;
существует конечный предел функции в точке ;
это предел равен значению функции в точке , т.е.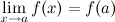
называется точкой разрыва функции.
Если в точке существуют конечные пределы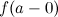 
и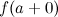 
, такие, что 
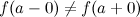, то точка называется точкой разрыва первого рода.
Если хотя б один из пределов 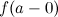или 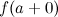не существует или равен бесконечности, то точка называется точкой разрыва второго рода.
Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции в точке : 
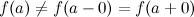или функция не определена в точке , то точка называется точкой устранимого разрыва.
|
|
34. Сравнение б/м функций. Теорема о связи б/б и б/м функции:
Функция 
называется бесконечно малой при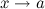 
(или в точке 
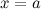), если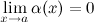 
Функции и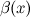 
называются б.м. одного порядка малости при 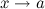, если 
Если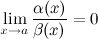 
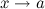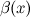, то является б.м. более высокого порядка при , чем , а 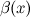- б.м. более низкого порядка по сравнению с : 
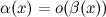при .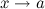
Если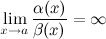 
, то - б.м. низшего порядка малости при 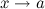по сравнению с .
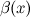Если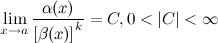 
, то называется б.м. порядка 
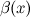по сравнению с при .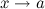
Если функция 
- функция бесконечно малая (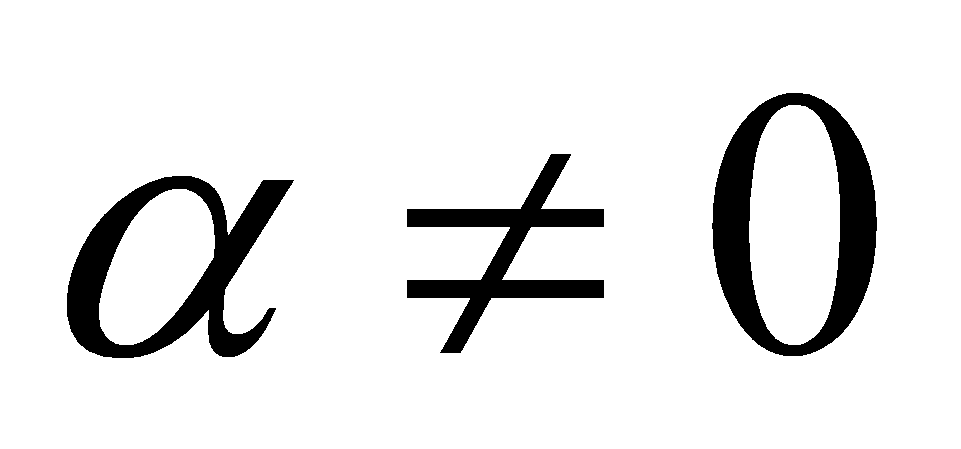
), то функция 
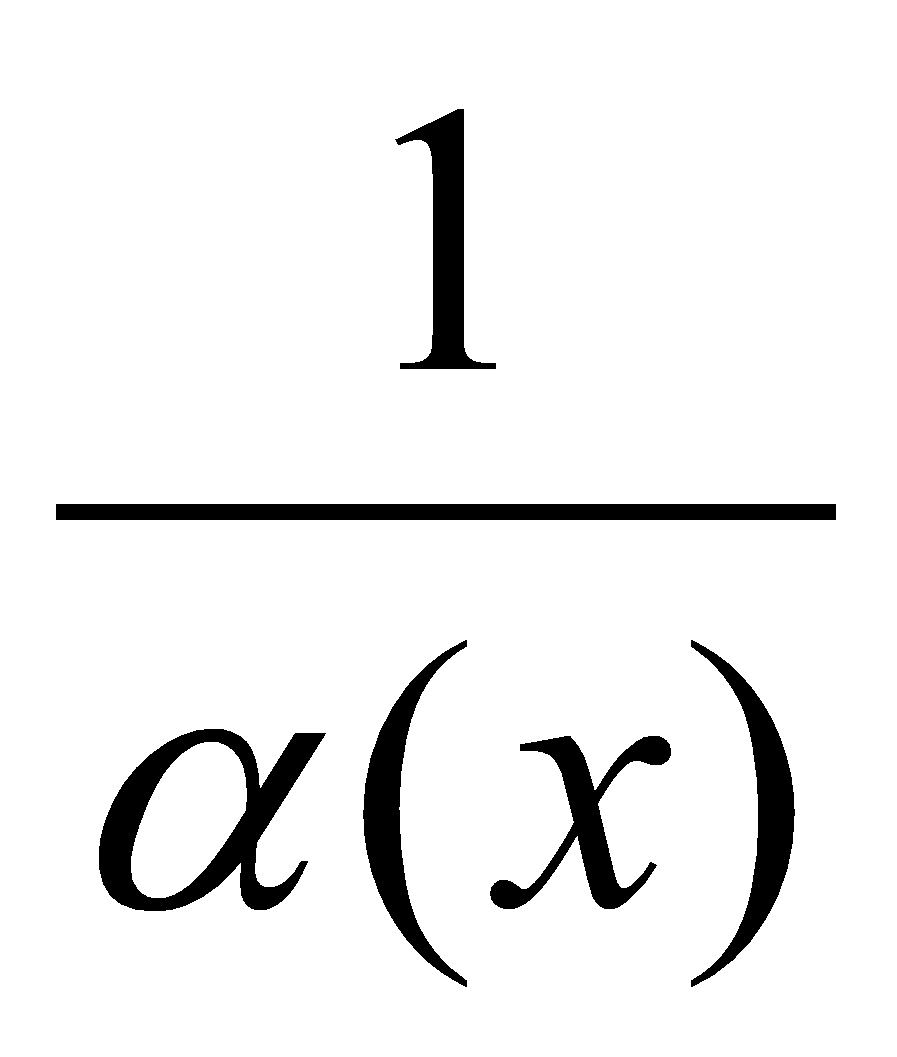есть бесконечно большая функция и наоборот.
35. Теоремы об эквивалентных б/м функциях:
Б.м. функции и 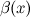называются эквивалентными или равносильными б.м. одного порядка при 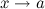, если 
Обозначают: 
при .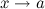
Разность двух эквивалентных б.м. функций есть б.м. функция более высокого порядка, чем каждая из них.
Сумма конечного числа б.м. функций разных порядков эквивалентна слагаемому низшего порядка.
Сравнение б/б функций.
Пусть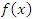 
и 
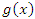– бесконечно большие функции при x → a. Рассмотрим возможные значения предела отношения этих функций:
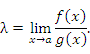
Если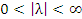 
, то функци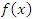и и 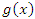называются бесконечно большими одного и того же порядка.
Функци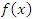и и 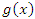называются эквивалентными бесконечно большими при x → a, если λ = 1. Для записи эквивалентности функций используется обозначение вида
Функция 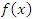называется бесконечно большой более высокого порядка по сравнению с 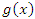при x → a, если λ = ∞; при этом говорят, что 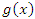имеет меньший порядок роста.
Есл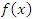и и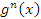 
представляют собой бесконечно большие функции одного и того же порядка, то функция 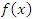называется бесконечно большой n-го порядка по сравнению с 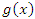. Например, функция 
является бесконечно большой 4-го порядка по сравнению с 
при x → ∞.
Если λ = 0, то функция 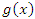является бесконечно большой более высокого порядка по сравнению с 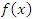при x → a.
|
|
37.