Теорема Ферма.
Если функция определена в некоторой окрестности точки, принимает в этой точке наибольшее (наименьшее) значение и имеет конечную или определенного знака бесконечную производную, то эта производная равна нулю.
Предположим, что функция 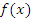 дифференцируема в точке
дифференцируема в точке 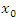 и
и  . Если
. Если 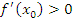 , то функция
, то функция 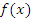 возрастает в окрестности точки
возрастает в окрестности точки 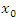 ; если
; если  , то функция
, то функция 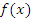 убывает в окрестности точки
убывает в окрестности точки 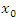 . В обоих случаях
. В обоих случаях 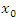 не является точкой экстремума и, таким образом, допущение
не является точкой экстремума и, таким образом, допущение  приводит к противоречию с условиями теоремы.
приводит к противоречию с условиями теоремы.
Теорема Ролля.
Пусть функция  непрерывна на отрезке
непрерывна на отрезке 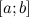 ; дифференцируема на интервале
; дифференцируема на интервале 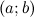 ;
;
на концах отрезка 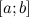 принимает равные значения
принимает равные значения 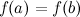 .
.
Тогда на интервале 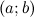 найдется, по крайней мере, одна точка
найдется, по крайней мере, одна точка 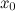 , в которой
, в которой 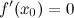 .
.
Если в граничных точках значения функций равны, то функция принимает свое макс или мин значение в одной из точек отрезка. Согласно теореме Ферма, производная в этой точке равна 0
Теорема Лагранжа
 Пусть функция
Пусть функция 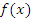 дифференцируема на интервале
дифференцируема на интервале 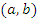 и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка
и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка  , что
, что
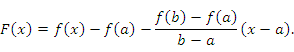 Доказательство. Рассмотрим вспомогательную функцию
Доказательство. Рассмотрим вспомогательную функцию
Эта функция непрерывна и дифференцируема в промежутке  ,
,
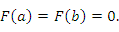 а на его концах принимает одинаковые значения:
а на его концах принимает одинаковые значения:
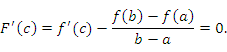 Тогда
Тогда 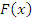 удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка
удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка  , в которой производная функции
, в которой производная функции 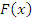 равна нулю:
равна нулю:
9. Теорема Коши. (Об отношении конечных приращений двух функций)
Если функции  и
и  : непрерывны на отрезке
: непрерывны на отрезке 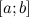 ; дифференцируемы на интервале
; дифференцируемы на интервале 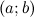 ;
;
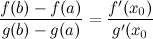 производная
производная 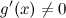 на интервале
на интервале 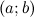 , тогда на этом интервале найдется по крайней мере одна точка
, тогда на этом интервале найдется по крайней мере одна точка 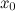 , такая, что
, такая, что
Формула Тейлора с остатком Пеано.

11. Выписать формулы Тейлора:
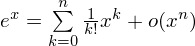
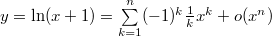
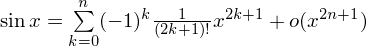
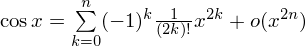
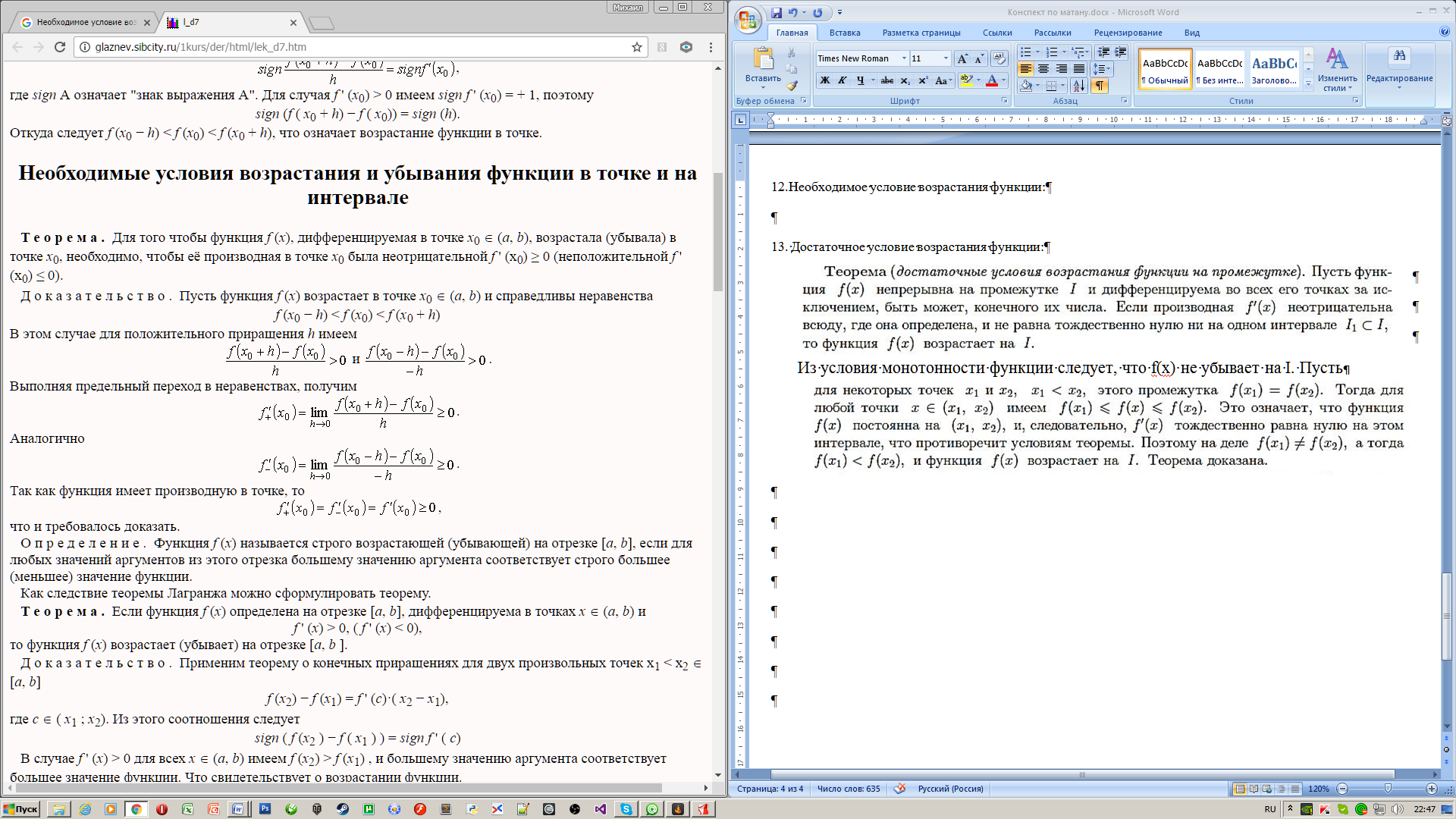 12.Необходимое условие возрастания функции:
12.Необходимое условие возрастания функции:
 13. Достаточное условие возрастания функции:
13. Достаточное условие возрастания функции:
 Из условия монотонности функции следует, что f(x) не убывает на І. Пусть
Из условия монотонности функции следует, что f(x) не убывает на І. Пусть
14. Необходимое условие существования экстремума:
Пусть функция y=f(x) дифференцируема на (a,b), число x0  (a,b) и f(x0) является экстремумом функции f. Тогда f'(x0) = 0.
(a,b) и f(x0) является экстремумом функции f. Тогда f'(x0) = 0.
Доказательство. Пусть f(x0) является максимумом функции f, тогда
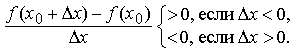
Переходя к пределу, получаем
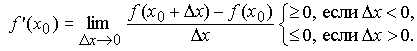
Так как по условию теоремы при x = x0 производная функции f существует, то f'(x0) = 0. Аналогично доказывается, что если f(x0) является минимумом функции f, то f'(x0) = 0.
 15. Достаточное условие экстремума по 1 производной:
15. Достаточное условие экстремума по 1 производной:
16. Достаточное условие экстремума по 2 производной:

 17. Достаточное условие выпуклости дважды дифференцируемой функции.
17. Достаточное условие выпуклости дважды дифференцируемой функции.
18. Необходимое условие существования точки перегиба:

19. Достаточное условие существования точки перегиба:

Определение предела числовой последовательности, теорема о единственности.

Теорема 1. Последовательность точек расширенной числовой прямой 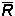 может иметь на этой прямой только один предел.
может иметь на этой прямой только один предел.
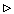 Допустим противное. Пусть существует такая последовательность xn
Допустим противное. Пусть существует такая последовательность xn 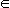
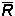 , n = 1, 2,..., что
, n = 1, 2,..., что 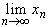 = a и
= a и 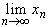 = b, причем a
= b, причем a 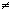 b, a
b, a 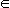
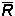 , b
, b 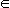
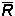 . Возьмем какие-либо непересекающиеся окрестности U = U(а) и V = V(b) точек а и b (рис. 49): U
. Возьмем какие-либо непересекающиеся окрестности U = U(а) и V = V(b) точек а и b (рис. 49): U  V =
V = 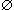 . Согласно определению предела вне окрестности U точки а, в частности в окрестности V точки b, содержится лишь конечное число членов последовательности {xn}. Однако точка b также является ее пределом, и потому в ее окрестности V должны находиться все члены последовательности {xn}, начиная с некоторого номера, а следовательно, бесконечно много ее членов. Получилось противоречие.
. Согласно определению предела вне окрестности U точки а, в частности в окрестности V точки b, содержится лишь конечное число членов последовательности {xn}. Однако точка b также является ее пределом, и потому в ее окрестности V должны находиться все члены последовательности {xn}, начиная с некоторого номера, а следовательно, бесконечно много ее членов. Получилось противоречие. 
21. Теорема о связи одностороннего предела с двусторонним:
Точка b 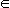 R является двусторонним пределом функции f(x) в конечной точке а
R является двусторонним пределом функции f(x) в конечной точке а 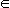 R тогда и только тогда, когда b является и левым, и правым пределами этой функции в точке а или ее окрестности.
R тогда и только тогда, когда b является и левым, и правым пределами этой функции в точке а или ее окрестности.
22. Теорема о пределе суммы:
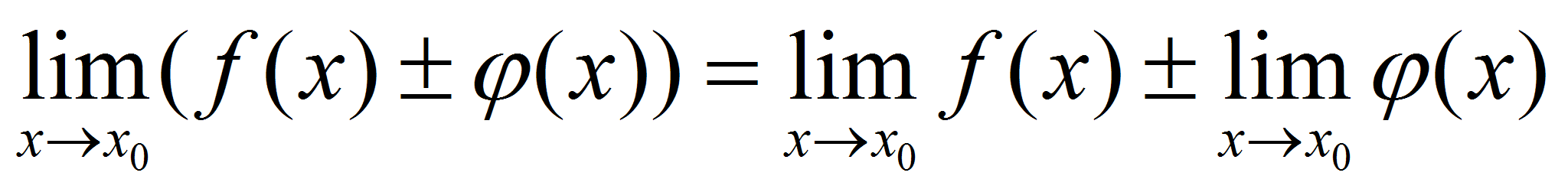 Предел суммы двух функций равен сумме их пределов:
Предел суммы двух функций равен сумме их пределов:
Доказательство:
Пусть 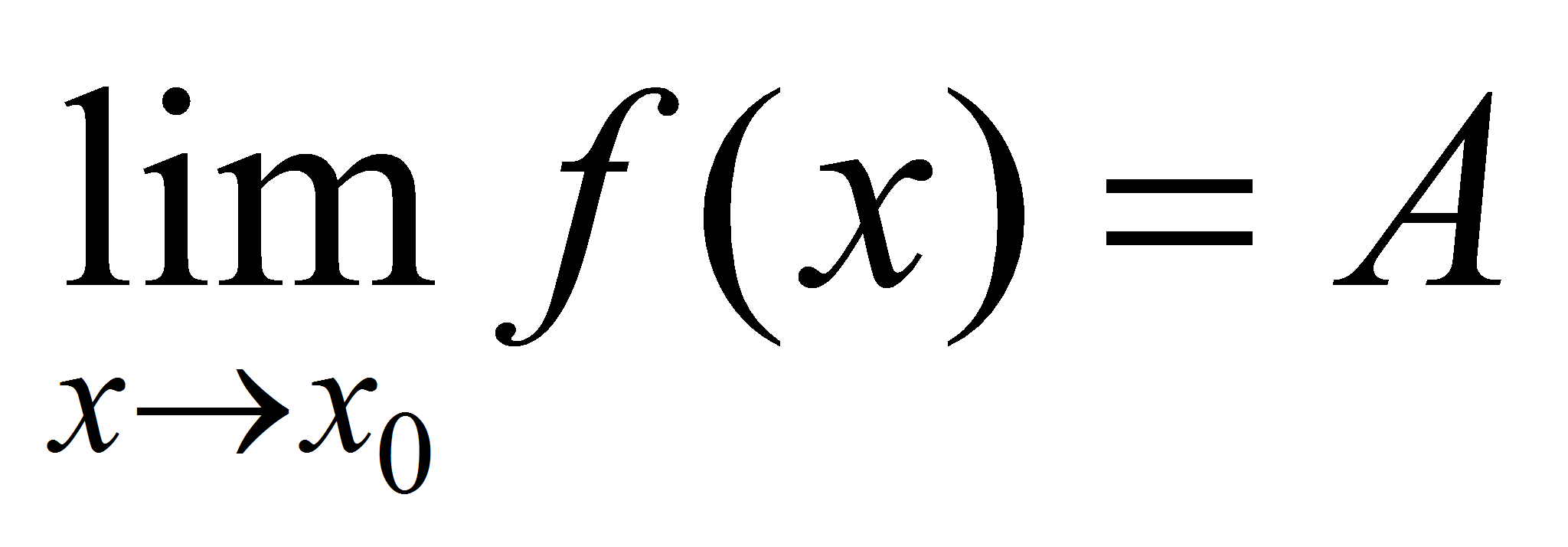 ,
, 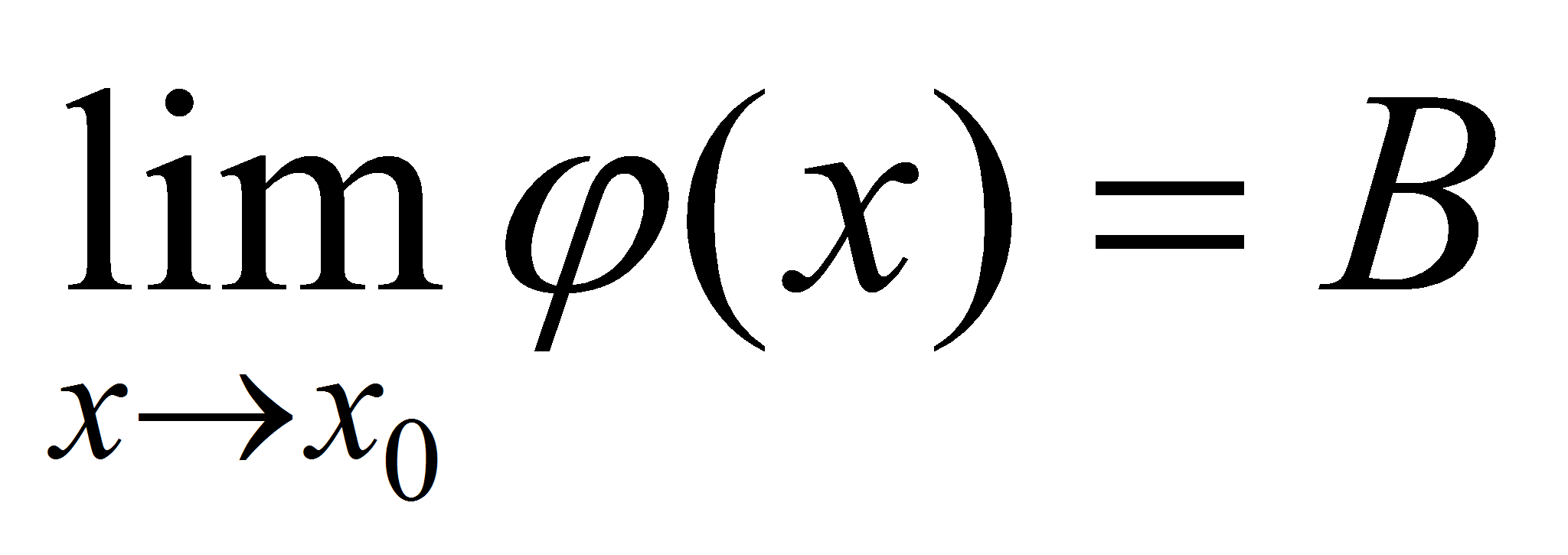 . Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать:
. Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать: 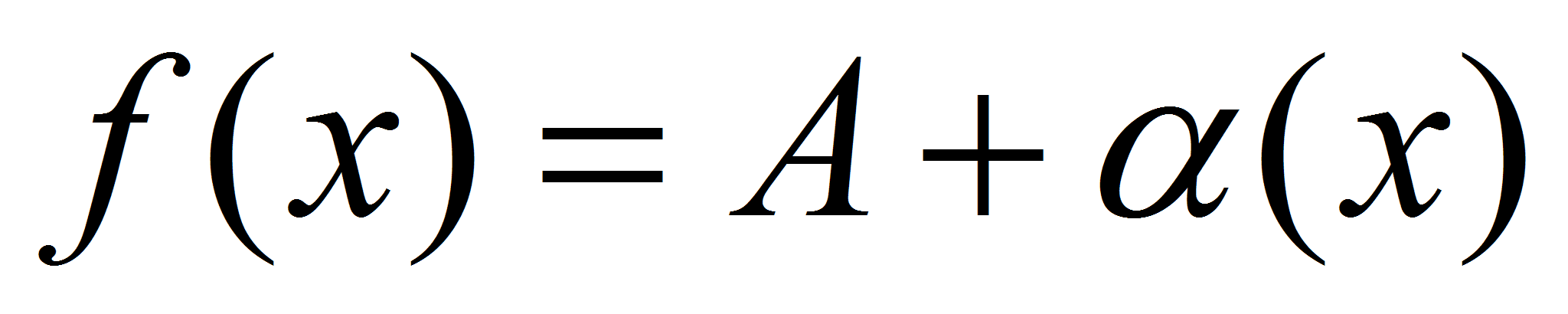 и
и 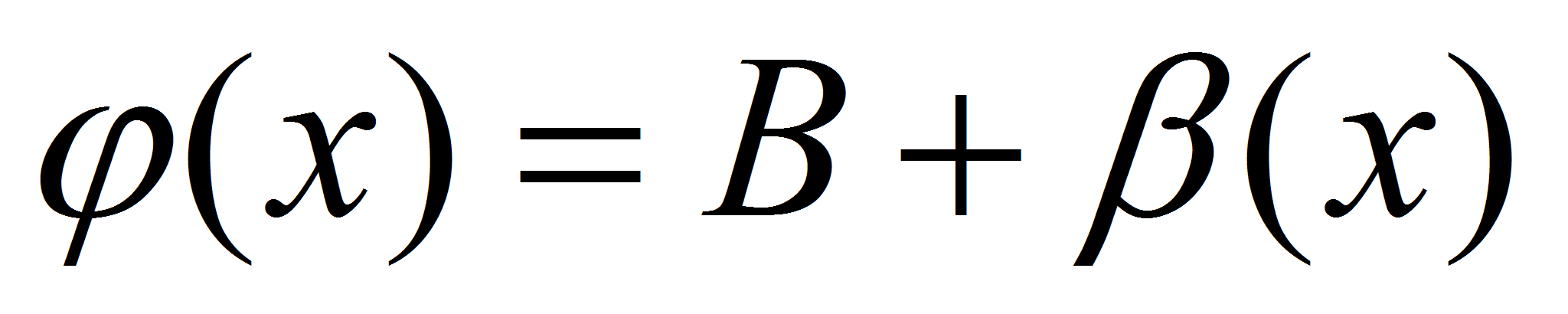 . Следовательно,
. Следовательно, 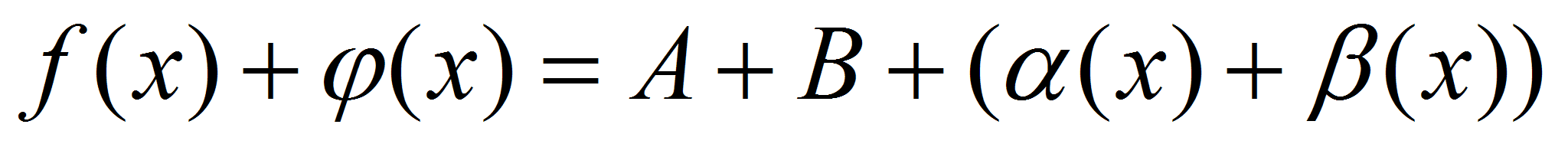 , где
, где 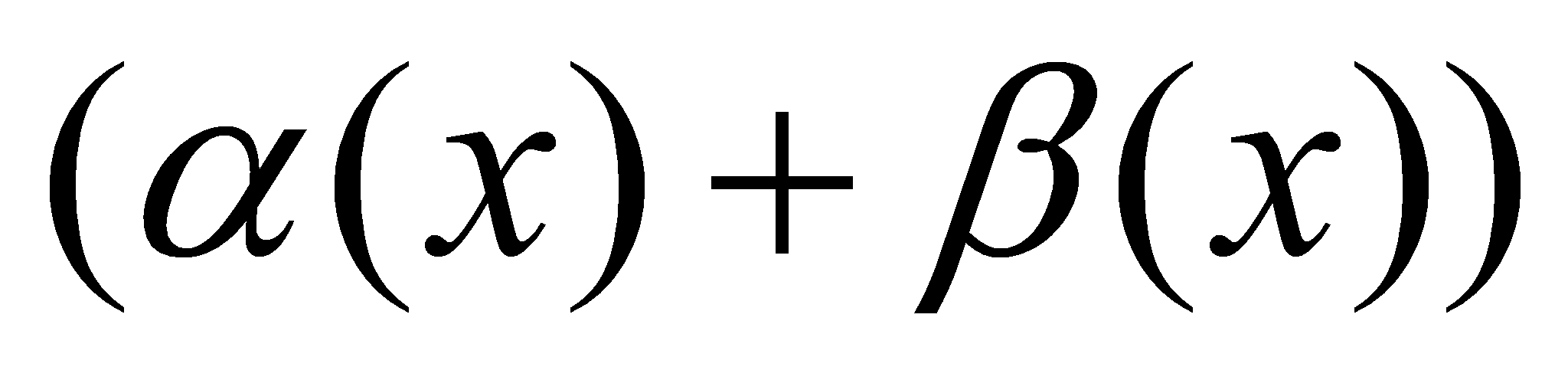 - бесконечно малая функция (по свойству бесконечно малых функций). Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать
- бесконечно малая функция (по свойству бесконечно малых функций). Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать 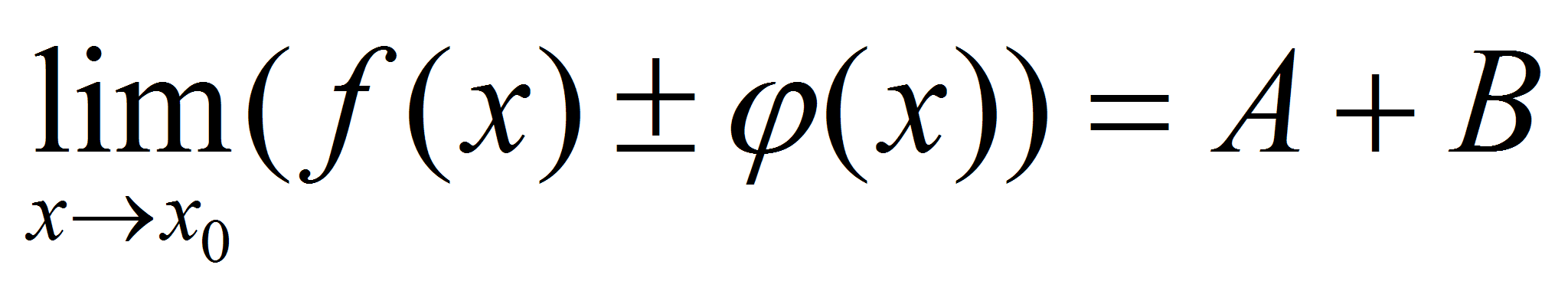 , или
, или 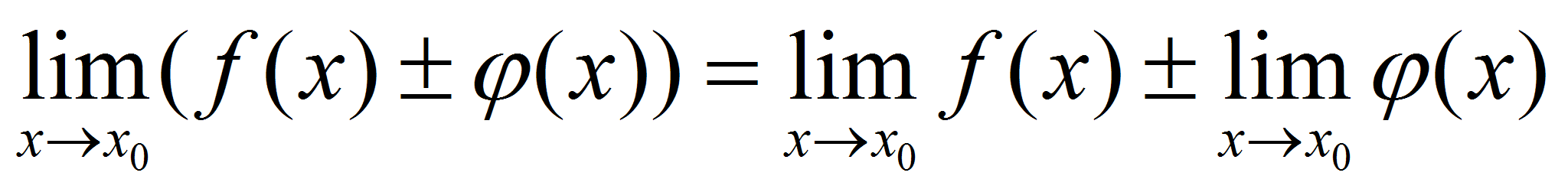 .
.
23. Теорема о пределе произведения:
Предел произведения двух функций равен произведению их пределов: 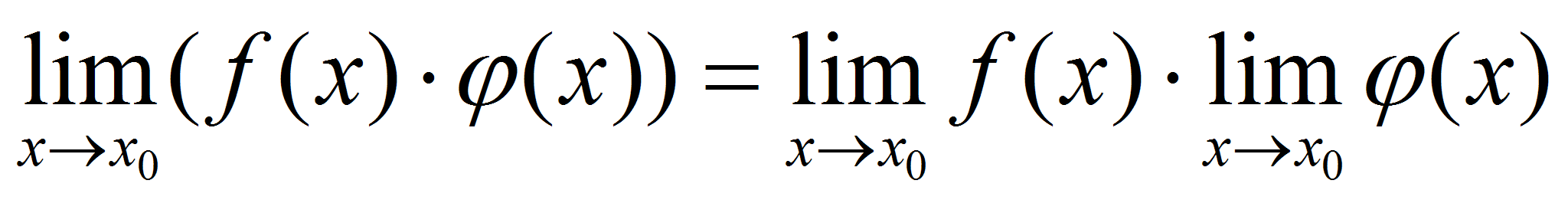
Доказательство:
Пусть 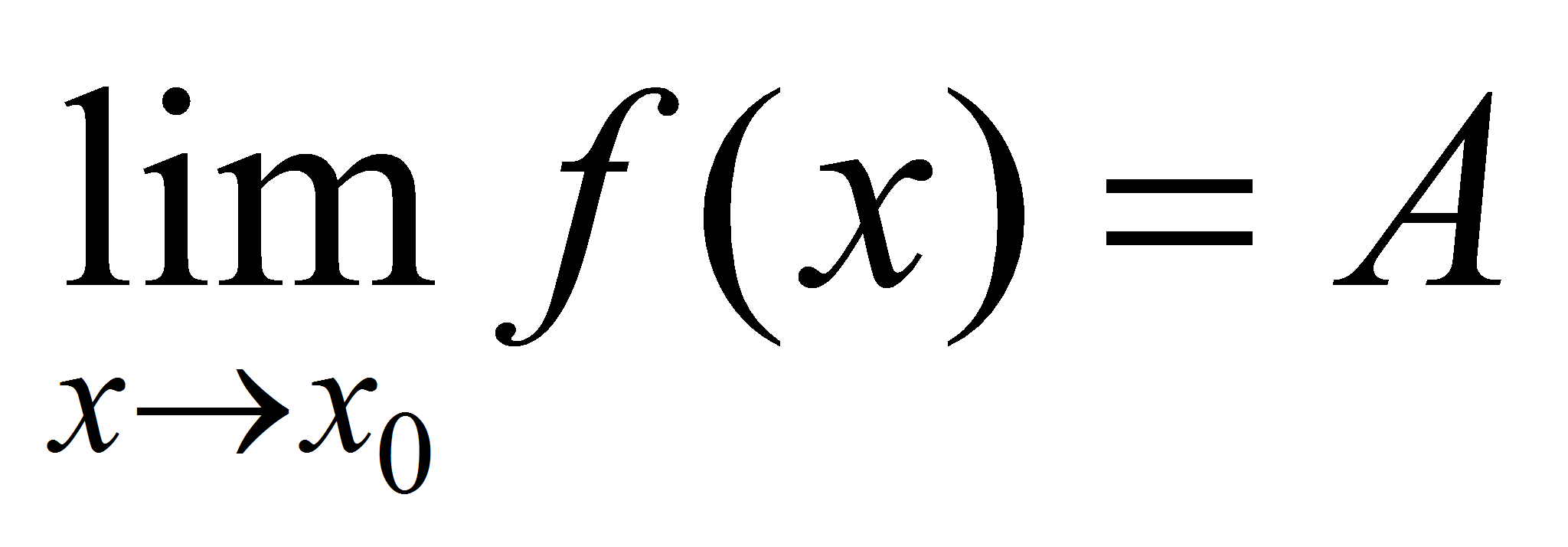 ,
, 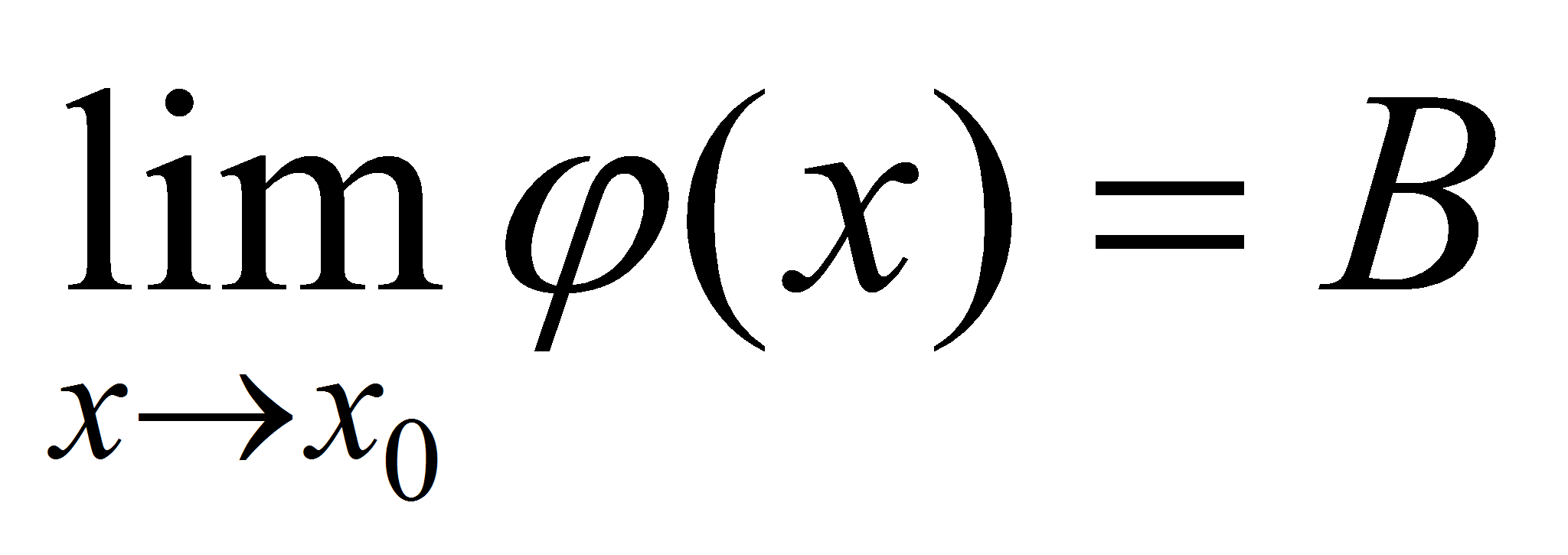 . Тогда
. Тогда 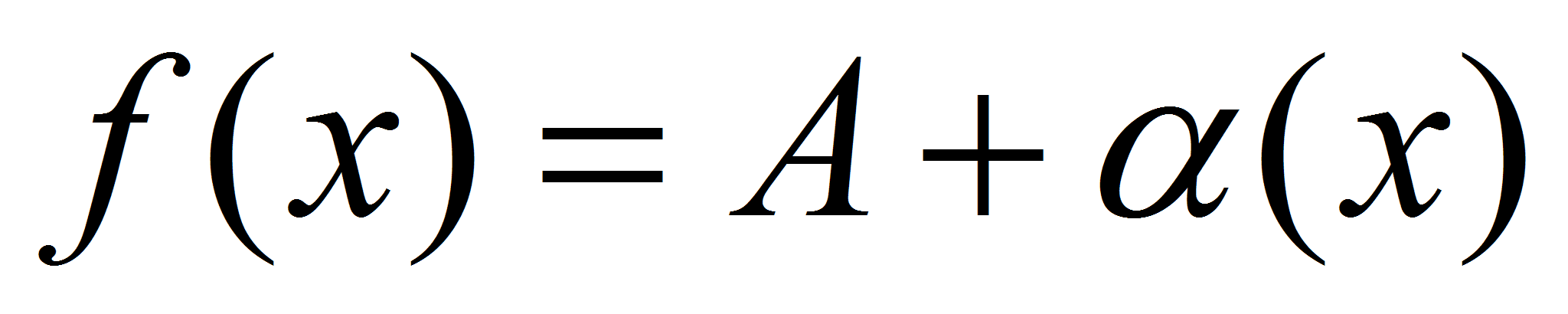 и
и 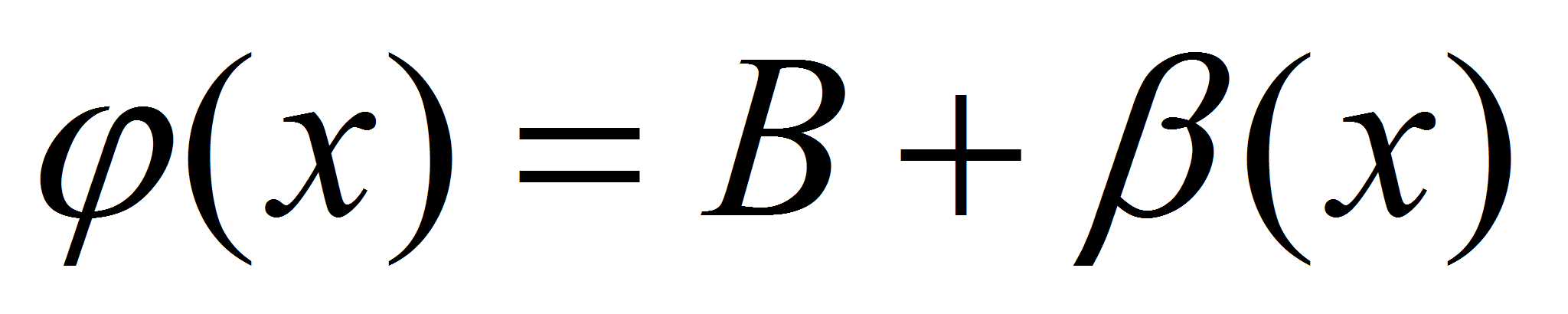 . Следовательно
. Следовательно
 ,
,
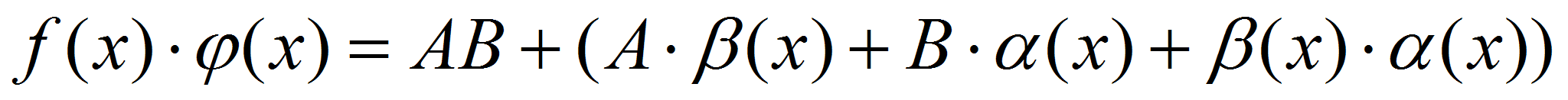 .
.
Выражения в скобках, по свойствам бесконечно малых функций, - бесконечно малая функция. Тогда 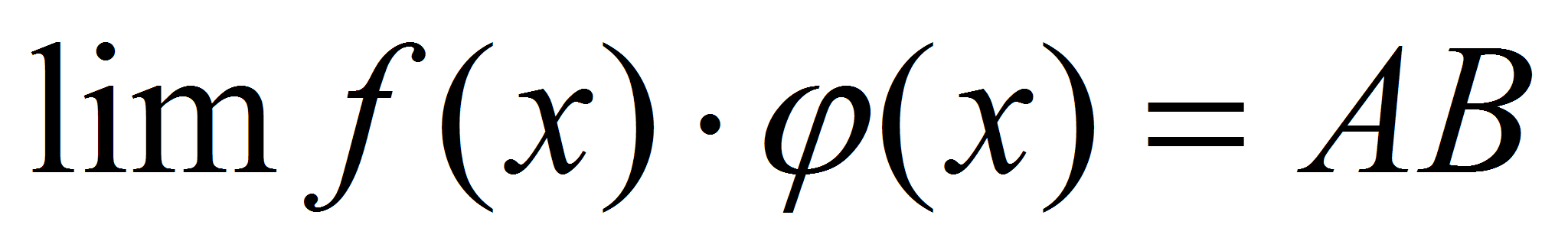 , т.е.
, т.е. 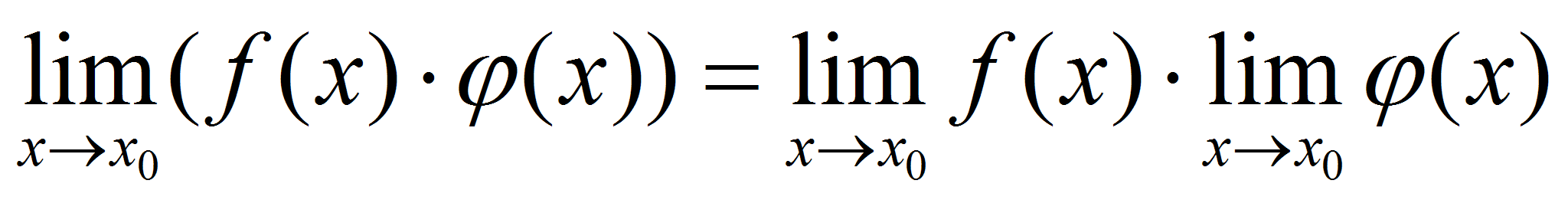 .
.
24. Теорема о пределе частного:
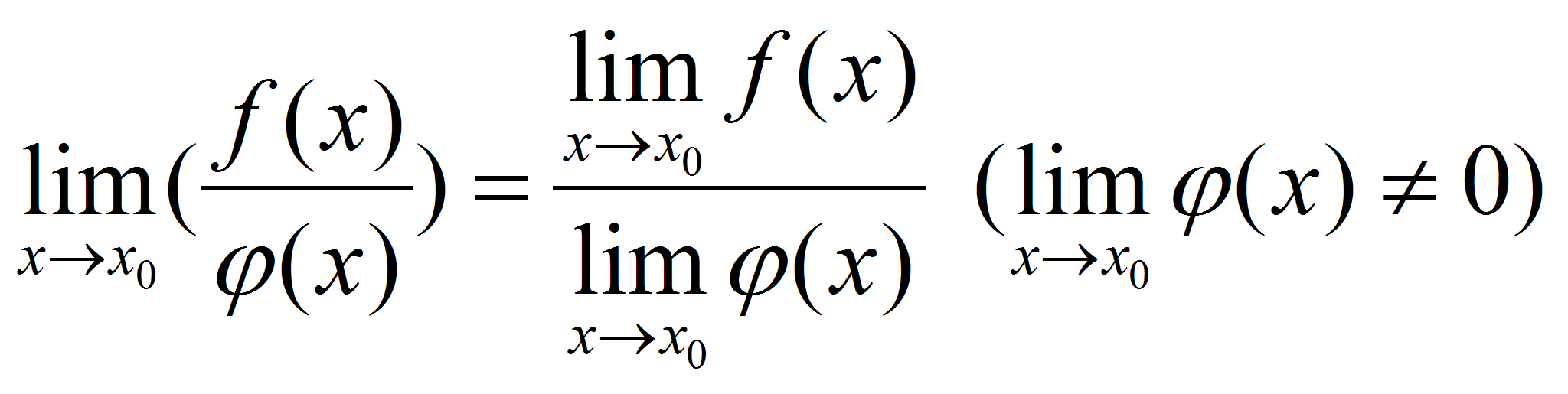 Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен 0:
Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен 0:
Доказательство:
Пусть 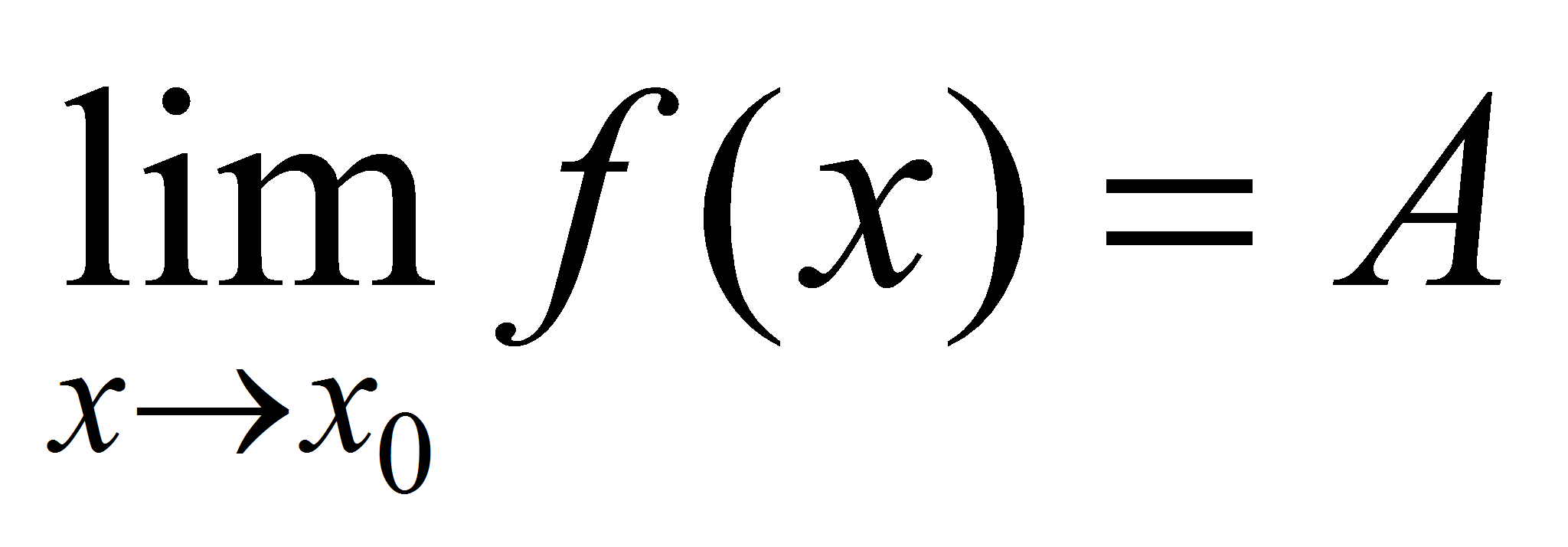 ,
, 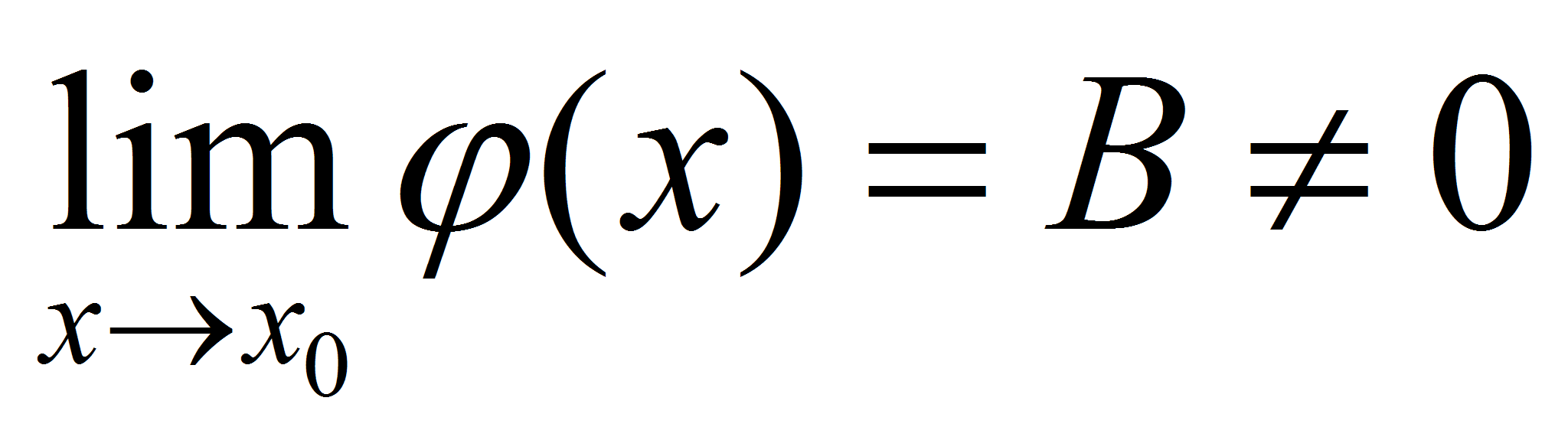 .
.
Тогда 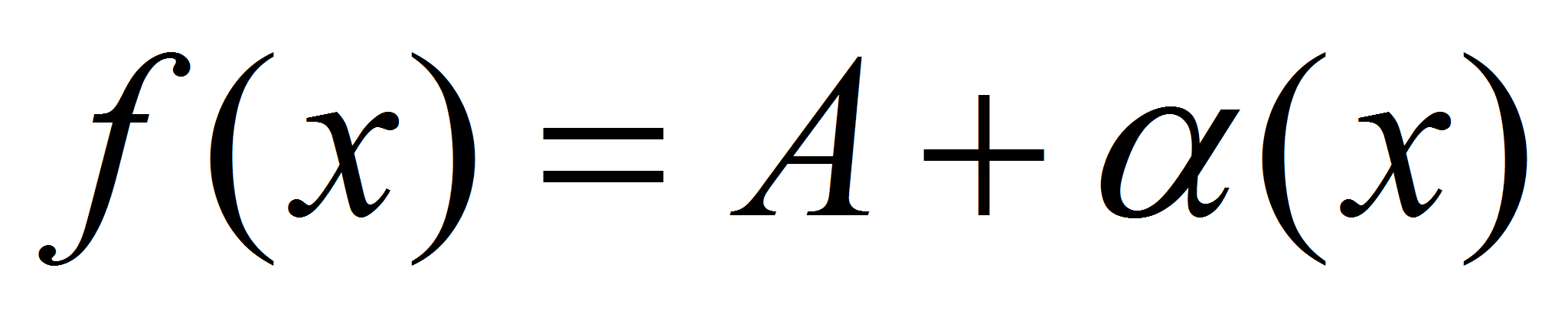 и
и 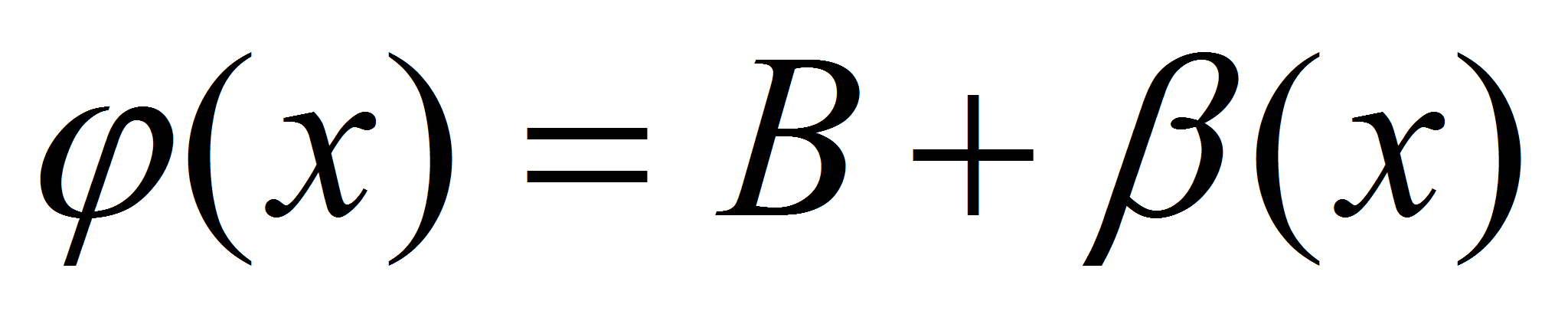 . Тогда
. Тогда 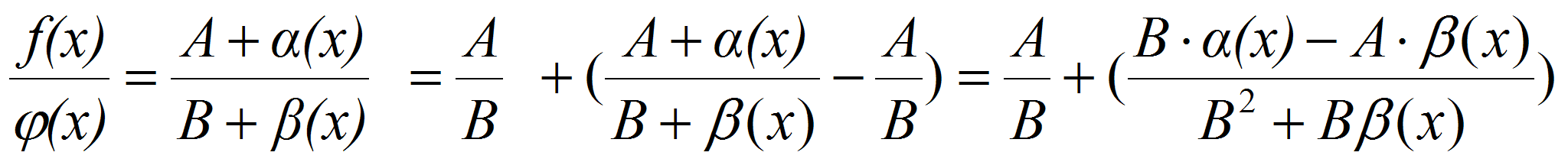 . По свойствам бесконечно малых функций, второе слагаемое – бесконечно малая функция.
. По свойствам бесконечно малых функций, второе слагаемое – бесконечно малая функция.
Поэтому 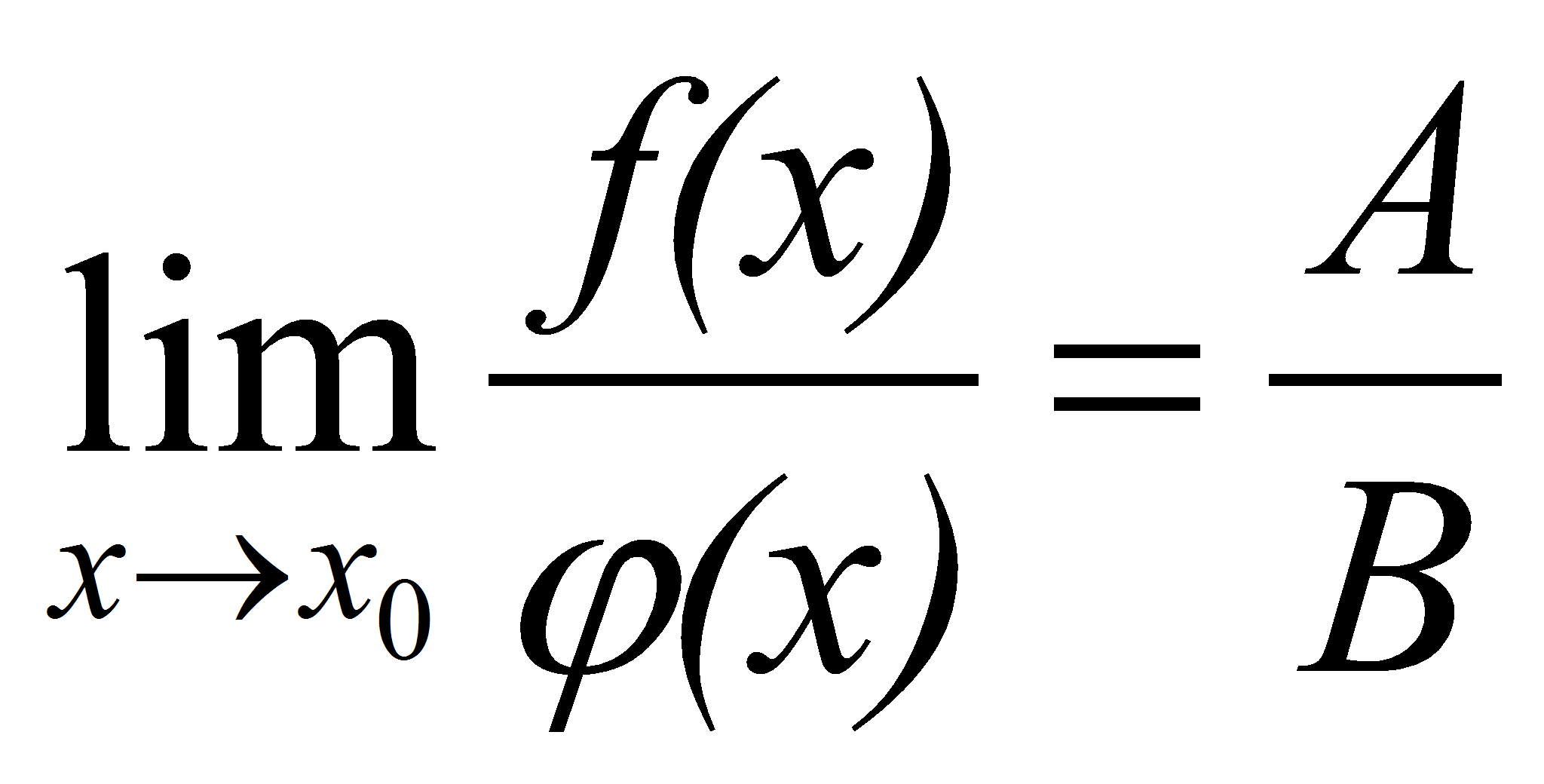 , т.е.
, т.е. 
25. Первый замечательный предел: 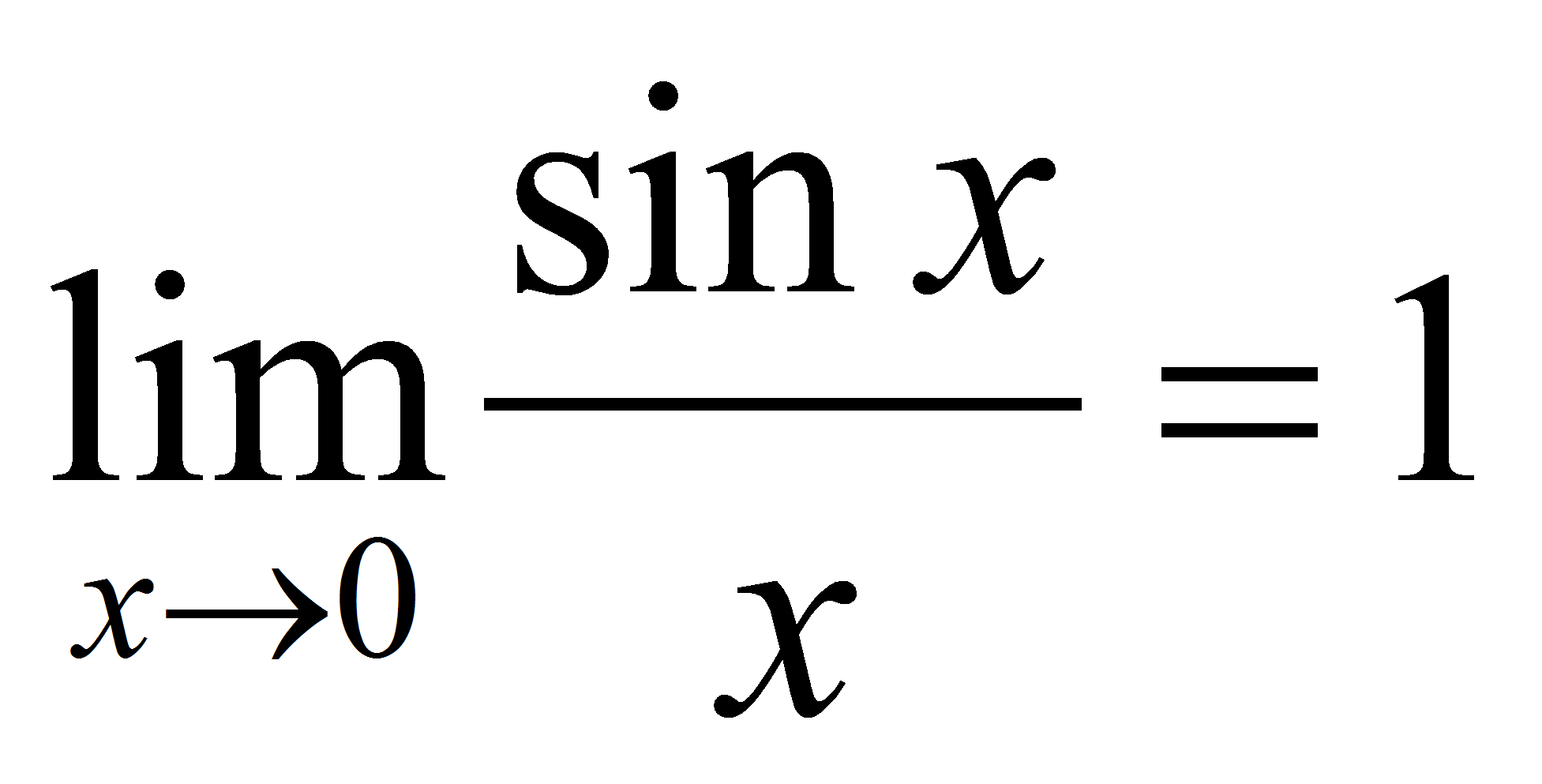
26. Второй замечательный предел: