БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ
КАФЕДРА ЭНЕРГОФИЗИКИ
Л а б о р а т о р н а я р а б о т а
Определение коэффициента теплопроводности сравнительным методом в стационарном тепловом режиме
М и н с к – 2009
Лабораторная работа №
Определение коэффициента теплопроводности сравнительным методом в стационарном тепловом режиме.
Цель работы. Ознакомление с теоретическими и экспериментальными основами определения коэффициента теплопроводности в стационарном режиме сравнительным методом.
Краткая теория.
Все методы определения теплофизических свойств основаны на решения дифференциального уравнения теплопроводности
 (1)
(1)
при заданных краевых условиях. Если свойства не зависят от температуры, то уравнение (1) упрощается:
 (2)
(2)
где 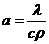 - коэффициент температуропроводности,
- коэффициент температуропроводности, 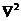 - оператор Лапласа.
- оператор Лапласа.
В стационарном тепловом режиме 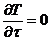 . Поэтому (2) можно записать в виде
. Поэтому (2) можно записать в виде
 (3)
(3)
Уравнение (3) называется уравнением Лапласа. Решения (3) широко используется для описания стационарных температурных полей, потенциального движения несжимаемой жидкости и многих других явлений.
Наиболее просто находятся соответствующие решения (3), когда температура зависит только от одной координаты, то есть в случае одномерных температурных полей.
Для тел простейшей геометрической формы – неограниченной пластины, полого цилиндра и полого шара уравнение Лапласа имеет вид
 (4)
(4)
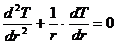 (5)
(5)
 (6)
(6)
Дифференциальные уравнения (4) – (6) позволяют рассчитать температурные поля при заданных граничных условиях в указанных выше телах. Используя закон Фурье
 (7)
(7)
(для пластины  ,
,  - тепловой поток;
- тепловой поток;  - коэффициент теплопроводности), можно найти тепловые потоки.
- коэффициент теплопроводности), можно найти тепловые потоки.
Обратная задача теплопроводности сводится к определению коэффициента теплопроводности по заданному тепловому потоку и известному значению  .
.
Использование системы тел (составная пластина, цилиндр), теплофизические свойства одного из которых предполагаются известными, позволяет исключить непосредственное определение теплового потока. Материал с известными свойствами часто называется эталонным (эталоном). Так как в стационарном состоянии тепловой поток, проходящий через каждое из тел системы, будет одинаковым и постоянным во времени, то используя (7), можно записать следующее соотношение
 (8)
(8)
где «э» означает «эталон». В данной работе в качестве эталона используется плексиглас (полиметилметакрилат), у которого при комнатной температуре  .
.
Исследование проводится с системой двух пластин (эталон – исследуемый материал) и полым составным цилиндром. На ограничивающих поверхностях задаются постоянные, но неодинаковые температуры (см. рис. 1).
Решение (4) и (5) можно записать так:
 (9)
(9)
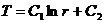 (10)
(10)
Для системы пластин расчетная формула совпадает с (8), то есть
 (11)
(11)
Смысл обозначений пояснен на рис. 1.
Для системы цилиндрических тел, для каждой области в отдельности (см. рис. 1) на основании (7) и (10) можно записать следующие выражения:
 (12)
(12)
 (13)
(13)
Соотношения (12) и (13) можно преобразовать, введя тепловой поток на единицу длины
 (14)
(14)
 (15)
(15)
Сравнивая (14) и (15), находим:
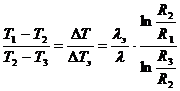 (16)
(16)
Таким образом, коэффициенты теплопроводности пластины и цилиндра находятся из формул (11) и (16).
Важными понятиями теории теплопроводности являются понятия термического сопротивления и эффективного значения коэффициента теплопроводности.
Термическое сопротивление определяется как величина  . В случае системы пластин общее термическое сопротивление равно сумме термических сопротивлений отдельных пластин, то есть
. В случае системы пластин общее термическое сопротивление равно сумме термических сопротивлений отдельных пластин, то есть
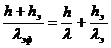 (17)
(17)
где  - эффективное значение коэффициента теплопроводности. Для цилиндрической системы получается следующее выражение:
- эффективное значение коэффициента теплопроводности. Для цилиндрической системы получается следующее выражение:
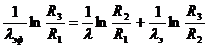 (18)
(18)
Описание экспериментальной установки.

Рис. 1. Схема экспериментальной установки.
Принципиальная схема установки показана на рис. 1. Выше было указано, что в качестве эталона используется плексиглас, механически контактирующий с испытуемым материалом. При исследовании плоскопараллельных квадратных или круглых пластин эталон помещается между двумя пустотелыми блоками, образующими струбцину и позволяющими обеспечить лучший механический контакт пластин. В цилиндрическом варианте испытуемым материалом является кварцевый песок, который находится между двумя цилиндрическими поверхностями. Наружный цилиндрический слой выполнен из плексигласа (эталон), внутренний представляет металлическую трубку, соединенную с термостатом и одним из блоков «плоской» системы. С помощью термостата задается температура, превышающая комнатную на 5 – 10 °C. Наружная поверхность цилиндрической системы и один из блоков плоской системы во время эксперимента находятся при комнатной температуре. Таким образом, в системах создаются температурные перепады. Для измерения этих перепадов используются хромель-алюмелевые термопары и гальванометр. При испытании пластин используются три термопары. Две из них зачеканены в металлических блоках, третья – на эталоне. Концы термопар выведены на клеммы и обозначены через 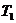 ,
,  ,
,  .
.