РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СЛУЧАЙНЫХ ВЕЛИЧИН

ОСНОВЫСтатистической теории РАДОИСИСТЕМ

Пособие для решения задач

 

Часть 1

Теория вероятностей

 

 

Таганрог 2008

ОСНОВНЫЕ ТЕОРЕМЫТЕОРИИ ВЕРОЯТНОСТЕЙ

Теоретические сведения

Основными понятиями теории вероятностей являются понятие события и понятие вероятности. Событие это явление, которое в результате некоторого действия может либо произойти, либо нет. Различают достоверные, невозможные и случайные события. [1, 2, 3]. Достоверные события обозначаются буквой U, невозможные – V, aслучайные – буквами А, В, С,.... Мерой случайности события является вероятность его появления P(A). Вероятность достоверного события принимается за единицу, а вероятность невозможного – за нуль:

P(U) = 1, P(V) = 0.

Таким образом, вероятность случайного события A изменяется в пределах от 0 до 1:

0<P(A)<1.

Наряду с одиночными событиями рассматривают группу (множество) событий. В группе событий помимо вероятности появления каждого из них необходимо характеризовать взаимную связь между событиями в группе. События в группе могут быть независимыми или зависимыми между собой. Если всякий раз, когда происходит событие А, происходит так же событие В, то говорят, что событие A влечет за собой событие и такое явление обозначают AB. Если A Ì B и в то же время В Ì А, то говорят, что события А и В равносильны, и обозначают А = В. В этом случае P(A) = P(B).

Суммой (объединением) множества событий А,В,С,... называют такое событие, которое происходит тогда и только тогда, когда происходит по крайней мере одно («хотя бы одно») из этих событий. Сумма событий А, В, С,... обозначается выражениями A + B + С + … или A U B U С U…. Если событие в группе обозначить А_k (k=1,2, …,M) то сумма этих событий обозначается или .

Непосредственно из определения суммы событий вытекают следующие соотношения:

A+A=A; A+U=U; A+V=А,

а также переместительный и распределительный (коммутативный) законы:

А+В=В+А; (А + В)+С=А + (В + С).

Произведением (или совмещением, или пересечением) событий А,В,С... называется событие, происходящее тогда и только тогда, когда все события происходят вместе («одновременно»). Произведение событий обозначают ABC … или или .

Для произведения событий очевидны следующие соотношения:

АA = A; AV = V; AU = A,

а также перемести тельный и распределительный (коммутативный) законы:

АВ = ВА; (АВ)С= А(ВС).

Для операций умножения и сложения событий, применяемых совместно, справедлив обычный распределительный (дистрибутивный) закон

(A+ В)С=АС+ВС

и так называемый «второй распределительный закон» [3]

АВ + С=(А + С)(В +С).

События А,В,С,... образуют полную группу событий, если в результате действия непременно должно появиться хотя бы одно из них. Другими словами, сумма событий, образующих полную группу, является достоверным событием, т. е.

А + В +С+...= U.

События а и В называют несовместными (или несовместимыми), если их совместное появление невозможно, т. е. если

АВ=V.

Два несовместных события, образующих полную группу, называются противоположными (или дополнительными) событиями. Событие, противоположное событию А, обозначается .

Для противоположных событий справедливы формулы:

(1.1)

Нетрудно заметить, что для противоположных событий эти формулы аналогичны соответствующим формулам булевской алгебры (алгебры логики). Противоположному событию соответствует операция логического отрицания (инверсии), сумме событий – логическая операция “ИЛИ” (дизъюнкция), произведению – логическая операция “И” (конъюнкция).

Если явление имеет N равновозможных исходов, которые несовместны и составляют полную группу (такую ситуацию называют схемой случаев), то вероятность Р(А) наступления события А определяется формулой

,

где п – число исходов, которые приводят к наступлению события А.

Таким образом, для нахождения вероятности Р(А) в рассматриваемом случае необходимо найти числа N и n и вычислить их отношение. При решении задач такого типа общие способы для нахождения чисел N и п неизвестны. Часто для вычисления указанных чисел полезно использовать методы комбинаторной алгебры: размещения, перестановки, сочетания.

Размещениями из N элементов по m называют такие их комбинации, которые различаются друг от друга или самими элементами или их порядком. Например, два элемента из трех a, b, c можно разместить следующими способами: ab, ac, bc, ba, ca, cb. Число возможных размещений определяется формулой

. (1.2)

Перестановками из N элементов называют такие их комбинации, которые различаются друг от друга только порядком входящих в них элементов. Например, возможные перестановки из трех элементов a, b, c: abc, acb, bac, bca, cab, cba. Число возможных перестановок определяется формулой

. (1.3)

Если среди элементов a, b, c … имеются одинаковые (a повторяется α раз, b – β раз, с – γ раз и т.д.), то

. (1.4)

Сочетаниями из N элементов по m называют такие их комбинации, которые различаются друг от друга только самими элементами, а порядок элементов во внимание не принимается. Например, два элемента из трех a, b, c можно сочетать следующими способами: ab, ac, bc. Число возможных сочетаний определяется формулой

. (1.5)

Для вычисления N! и m! при большихзначениях N и m удобно использовать приближенную формулу Стирлинга

 

, (1.6)

которая дает приемлемую точность и при небольших значениях k [3]. Например, при k > 1 ее относительная погрешность не превышает 10%, а при k > 10 – 1%, а при k > 100 – 0,1%.

Понятие равновозможности событий иногда применяют к опытам с бесконечным числом исходов, когда числа N и п в формуле (1) определить невозможно: проще вычислить саму вероятность события, а не порознь числа п и N.

В таких случаях пользуются геометрическими интерпретациями возможных исходов исследуемого явления, и вероятность наступления события A определяют по формуле

, (1.7)

где G – геометрическая мера (длина отрезка, площадь фигуры, объем тела и т. д.) всей области возможных исходов исследуемого явления; g – геометрическая мера части той области G, попадание в которую благоприятствует событию А.

Нахождение вероятностей сложных событий (например, появления той или иной цепочки событий, суммы или произведения событий) базируется на использовании основных теорем теории вероятностей (теоремы сложения и умножения вероятностей и их следствий).

Согласно теореме сложения вероятностей вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения:

Р(А+В)=Р(А) + Р(В)-Р (AВ). (1.8)

Если события A и В несовместны, то

Р(А+В) = Р (A)+ Р(В).

Эти формулы обобщаются на сумму любого числа событий.

Сумма вероятностей несовместных событий, составляющих полную группу, равна единице:

.

Сумма вероятностей двух противоположных событий равна единице:

 

По теореме умножения вероятностей вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что произошло первое:

Р(АВ) = Р(А)Р(В|А) = Р(В)Р(А|В), (1.9)

где Р(А|В) – условная вероятность события A, т. е. вероятность появления события А приусловии,что произошлособытие В.

Если событие А статистически не зависит от события В, то Р(А |В) = Р(А). В этом случае события А и В называют независимыми. Для независимых событий A и В

 

Р(АВ) = Р(А)Р(В). (1.10)

 

Последние две формулы можно обобщить на N событий A ₁ A ₂,..., A _N:

Теоремы сложения и умножения вероятностей совместного используются при решении многих практических задач. Одним из важных приложений этих теорем является оценка надежности систем.

Надежность системы (или ее элемента) оценивают по вероятности того, что система (элемент) в течение установленного времени будет работать без отказов.

При объединении нескольких элементов в систему они могут соединяться параллельно, последовательно, либо использоваться их смешанное соединение. При параллельном соединении отказ системы возможен только при одновременном отказе всех элементов, а при последовательном система отказ системы происходит при отказе любого элемента.

Вероятность безотказной работы системы при параллельном соединении k элементов и независимых отказах можно рассчитать по формуле

, (1.11)

где p_i – вероятность безотказной работы i -ro элемента. С ростом k произведение в последней формуле стремится к нулю, а P – к единице. Следовательно, с увеличением числа параллельно включенных элементов надежность системы возрастает.

Вероятность безотказной работы системы при последовательном соединении k элементов при независимых отказах вычисляется по формуле

. (1.12)

С увеличением числа последовательно включенных элементов надежность системы убывает.

Во многих ситуациях то или иное событие А может появиться лишь как случайное следствие одного из несовместных событий H_i, (i = 1, 2,..., N), которые входят в некоторую полную группу событий и называются гипотезами. В таких случаях безусловная вероятность Р(А) события А при известных вероятностях гипотез Р(Н_i) и условных вероятностях Р(А|H_i) определяется по формуле полной вероятности:

(1.13)

При этих же данных, т. е. известных вероятностях P(H_i) и Р(А|H_i), можно найти вероятностей гипотез H_i, если событие А уже произошло. Задачи подобного типа решаются с помощью теоремы гипотез (или формулы Байеса)

 

. (1.14)

Вероятность P(H_i) называется априорной (или доопытной), а P(H_i|A) – апостериорной (послеопытной) или обратной вероятностью.

Формула Байеса лежит в основе ряда алгоритмов принятия решений в статистической теории радиосистем при обнаружении и оценке параметров сигналов (так называемые байесовские методы и алгоритмы).

В теории передачи сообщений, теории стрельбы, контроле качества продукции и т. д. одной из наиболее распространенных задач является нахождение вероятности появления некоторого количества событий в результате серии опытов, в каждом из которых наблюдаемое событие может произойти с некоторой вероятностью p_i. Проще всего такая задача решается, если опыты являютсянезависимыми (т. е. вероятность появления события не зависит от того, какие исходы имели другие опыты) и однородными (т.е. вероятность появления события не изменяется от опыта к опыту). Способ решенияподобных задач дает теорема о повторении опытов (теорема Я. Бернулли).

Вероятность Р_n(k) того, что при N независимых опытах (испытаниях) событие А появится ровно k раз, если при каждом опыте вероятность события А одинакова и равна р, определяется формулой Я. Бернулли

. (1.15)

 

При больших значениях N этой формулой пользоваться неудобно.В этомслучае для расчета вероятности P_N(k) можноприменять приближенныеформулы, основанные на асимптотических приближениях.

Если N велико, р мало, а Nр =l имеет конечное значение, тодля расчета P_N(k) можно пользоваться приближением Пуассона

. (1.16)

Погрешность этого приближения можно оценить по формуле

 

.

Когда npq не слишком мало, то применяется гауссова аппроксимация распределения Бернулли (формулаМуавра – Лапласа)

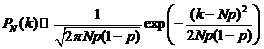. (1.17)

 

Погрешность гауссовой аппроксимации при вычислении вероятности P_N(k) можно оценитьпо формуле

 

Вероятность Р_N(k ³ m) того, что наблюдаемое событие в серии из N независимых опытов произойдет не менее m раз, если в каждом из опытов оно происходит свероятностью р, рассчитывается по формуле

. (1.18)

 

Вероятность Р_N (k ³1) появления события хотя бы один разпри N опытах равна

Р_N (k³ 1)= (1- (1- p)^N). (1.19)

Вероятность Р_N (k £ m) того, что при N независимых опытах рассматриваемое событие появится не более k раз, определяется выражением

. (1.20)

 

Вероятность Р_N (l £ k £ m) того, что при N независимых опытах рассматриваемое событие появится не менее l и не более k раз можно рассчитать по формуле

 

. (1.21)

 

При больших значениях N, l и m этой вычисления по этой формуле становятся громоздкими. В этом случае можно использовать ее гауссово приближение

, (1.22)

 

где

 

Количество опытов N, которые нужно выполнить для того, чтобыс вероятностью не меньшей Р ₁можно было утверждать, что данное событие произойдет хотя бы один раз, находится по формуле

. (1.23)

Эта формула получается из очевидного соотношения . Логарифмируя это выражение по произвольному основанию, получим рассматриваемую формулу.

Наиболее вероятное число появлений события А в N независимых опытах k₀ определяется из неравенства

(N+1)p - 1 £ k₀ < (N+1)p. (1.24)

Если же число (N+1)p целое, то неравенство определяет два значения наиболее вероятного числа k₀ появлений события А в N независимых опытах.

Теорема Бернулли представляет частный случай теоремы о повторении опытов. Известен ряд ее обобщений. Для статистической теории радиосистем представляют интерес два из них. Одно заключается в том, что вероятность наблюдаемого события р при проведении серииопытов изменяется от опыта к опыту. Второе состоит в том, что каждый опыт может иметь не два, а большее число исходов. Формулы для расчета соответствующих вероятностей можно найти в работе [3].

 

 

1.2. Задачи и ответы

1.2.1. Приведите примеры двух событий: а) равновозможных и несовместных, но не образующих полной группы; б) несовместных и образующих полную группу, но не равновозможных; в) равновозможных и образующих полную группу, но несовместных.

1.2.2. Система радиоконтроля с помощью трех сканирующих приемников (сканеров) осуществляет мониторинг радиоизлучений объекта. Для обнаружения нового сигнала достаточно, чтобы он был обнаружен любым из сканеров. Сканеры настроены так, что сигнал не может быть одновременно обнаружен двумя или тремя из них.

Выразить событие A, которое состоит в обнаружении сигнала системой через события A ₁, A ₂, А ₃ состоящие в обнаружении сигнала первым, вторым и третьим сканером соответственно.

Ответ: A = A₁+ А₂ + A₃.

 

1.2.3. Безотказная работа системы (событие A) возможна при условии, что исправны блоки Б1 (событие A ₁), Б2(событие A ₂),..., Бn(событие A _n).

Как связано событие A с событиями A_i, i = 1, 2,..., n.

Ответ:

 

1.2.4. Внутри квадрата, показанного на рис. 1.4, наугад выбирается точка. Событие А – попадание случайной точки в круг 1, событие В – попадание случайной точки в круг 2.

A B

Рис. 1.4.

 

Как соотносятся с событиями А и В события C, D, Е, F, G, Н, изображенные на рис. 1.5?

 

Рис. 1.5

Ответ:

 

1.2.5. А, В, С – три случайных события.

а) Найти выражение для события, состоящего в том, что из A, B, С произошло только событие A; б) произошли события A и В, но С не произошло; в) все три события произошли; г) произошло по крайней мере одно из этих событий; д) произошло по крайней мере два события; е) произошло одно и только одно событие; ж) произошли два и только два события; з) ни одно событие не произошло; и) произошло не более двух событий.

Ответ:

 

1.2.6. Проводится пуск трех ракет по одной и той же цели. Пусть события A ₁ попадание при первом пуске, Ā ₁–промах при первом пуске, A ₂ – попадание при втором пуске, Ā ₂– промах при втором пуске, А ₃– попадание при третьем пуске, Ā ₃– промах при третьем пуске.

Определите событие А, состоящее в том, что в цель попадет не менее двух ракет?

Ответ: .

 

1.2.7. Прибор состоит из двух блоков первого типа и трех блоков второго типа. События: A _i (i = 1, 2)–исправен i -й блок первого типа, B _j (j = 1, 2, 3) – исправен j -й блок второго типа. Прибор работает, если исправен хотя бы один блок первого типа и не менее двух блоков второго типа.

Выразить событие С, означающее исправность прибора, через события A_i и B_j.

Ответ: .

 

1.2.8. Известны события А, В и С, причем А Ì В. Определить сложные события АВ, А + В, ABC и А + В + С.

Ответ: АВ = A; A + В = В; AВС = АС; А + В + С = В + С.

 

1.2.9. Показать, что события:

а) – достоверно;

б) – невозможно.

 

1.2.10. Доказать следующие равенства:

 

1.2.11. Упростить выражения:

Ответ:

 

1.2.12. Игральная кость бросается один раз. Найти вероятность того, что выпадет: а) четное число очков; б) число очков, кратное трем; в) не более пяти очков.

Ответ: а) 1/2; б) 1/3; в) 5/6.

 

1.2.13. Две удаленные друг от друга однотипные радиостанции, настроены на 10 фиксированных частот, одинаковых у обеих станций.

Какова вероятность того, что при независимом произвольном выборе рабочих частот обе включенные радиостанции окажутся настроенными на одну и ту же частоту?

Ответ: 0,1.

 

1.2.14. Бросаются две игральные кости.

а) Найти вероятность того, что сумма выпавших очков равна 6; б) произведение выпавших очков равно 12; в) сумма выпавших очков кратна 5; г) на обеих костях выпадет одинаковое число очков; д) хотя бы на одной грани появится 5 очков.

Ответ: а) 5/36; б) 1/9; в)7/36; г) 1/6; д) 11/36.

 

1.2.15. В партии п стандартных приборов и m нестандартных. При контроле первые k приборов оказались стандартными.

Определить вероятность Р того, что следующий приборов будет стандартным.

Ответ: .

 

1.2.16. На пяти одинаковых карточках написаны цифры 1, 2, 3, 4 и 5. Две из них наугад вынимаются одна за другой.

а) Найти вероятность того, что сумма цифр на вынутых карточках является нечетным числом; б) вторая цифра меньше первой; в) вторая цифра больше первой ровно на 1.

Ответ: а) 0,6; б) 0,5; в) 0,2.

 

1.2.17. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наугад.

Определить вероятность Р того, что набраны нужные цифры.

Ответ:

 

1.2.18. Каждая из букв слова «событие» написана на одной из семи карточек. Карточки перемешиваются.

Какова вероятность Р того, что при извлечении трех карточек появится (в порядке их выемки) слово «быт»?

Ответ:

 

1.2.19. Каждая из цифр 1, 3, 5, 6 и 8 написана на одной из пяти карточек. Карточки перемешивают и раскладывают в ряд.

Найти вероятность того, что полученное пятизначное число будет делиться на четыре.

Ответ: 1/5.

 

1.2.20. Из группы, содержащей п карточек, перенумерованных от 1 до n, извлекают по одной карточке.

Найти вероятность Р того, что при n -кратном извлечении карточек их номера будут идти в возрастающем порядке, если: а) каждая вынутая карточка после просмотра ее номера возвращается обратно и карточки перемешиваются; б) извлеченные карточки обратно не возвращаются.

Ответ:

 

1.2.21. В монтируемый узел входят две одинаковые микросхемы. Параметры узла нарушатся, если обе они окажутся с пониженным входным сопротивлением. На складе 10 микросхем, из которых 3 имеют пониженное входное сопротивление.

С какой вероятностью окажутся нарушенными параметры при случайном выборе этих двух микросхем.

Ответ: 1/5.

 

1.2.22. На складе находится одних a блоков и b блоков других. Два блока повреждены.

Какова вероятность Р того, что повреждены разные блоки?

Ответ: .

 

1.2.23. В урне a белых и b черных шаров. Из урны вынимаются два шара.

а) Вычислить вероятность P того, что оба шара будут белыми; б) оба вынутых шара будут черными; в) один шар будет белым, а второй – черным.

Ответ:

 

1.2.24. На десяти из двадцати карточек написана цифра 1, а на остальных десяти – цифра 0. Пять карточек вынимаются наугад.

Найти вероятность Р того, что на двух карточках будет стоять цифра 1, а на трех – цифра 0 (безразлично, в каком порядке).

Ответ:

 

1.2.25. В урне а белых, b черных и с красных шаров. Из урны вынимают три шара.

Найти вероятность Р того, что среди них не будет шаров одинакового цвета.

Ответ:

 

1.2.26. В круг радиуса R вписан квадрат. Какова вероятность Р того, что взятая наудачу внутри круга точка, окажется и внутри квадрата?

Ответ:

 

1.2.27. Во время разговора абонента продолжительностью t сек поступил новый вызов.

Определить вероятность того, что к моменту вызова прошла большая часть разговора.

Ответ: 1/2.

 

1.2.28. На отрезке АВ длиной l случайно выбирается точка M. Положение точки на отрезке АВ равновероятно.

а) Найти вероятность Р того, что расстояние точки М от середины отрезка не превысит значения а.

б) Найти вероятность Р того, что площадь квадрата, построенного на AM, будет меньше l ²/4 и больше l ²/9.

Ответ: а) ; б) P=1/6.

 

1.2.29. С какой вероятностью корабль подорвется на мине при прохождении минного заграждения в одну линию, если интервал между минами l, ширина корабля a, диаметр мины d. Курс корабля составляет угол β с линией расположения мин.

Ответ: .

 

1.2.30. Последовательность радиоимпульсов с амплитудой U _s и гармоническая помеха с амплитудой U _n совпали во времени.Несущая частота радиоимпульсов равна частоте помехи.

Определить вероятность того, что амплитуда суммы сигнала и помехи окажется меньше произвольно заданного уровня U₀ (0 £ U₀ £ U_S), если сдвиг фаз между импульсов является случайным и с одинаковой вероятностью принимает любое значение из интервала 0 ¸ 2p.

Ответ: .

 

1.2.31. Посадочная система аэропорта обеспечивает заход самолетов на посадку с интервалом не менее 5 мин. По расписанию два самолета должны прибыть в аэропорт с разрывом 10 мин. Первый самолет может войти в зону посадки с отклонением от расписания в пределах ±10 мин, а второй – в пределах +5 мин. Величины отклонений от расписания в указанных пределах равновероятны.

Какова вероятность того, что второму самолету придется уходить в зону ожидания

Ответ: 0,25.

 

1.2.32. На отрезке АВ длиной l независимо друг от друга выбирают две случайные точки L и М. Положение каждой точки на отрезке АВ равновероятно.

а) Найти вероятность того, расстояние между точками L и М будет не больше некоторого значения a;

б) вероятность того, что точка L окажется ближе к точке А, чем точка М;

в) вероятность того, что точка L окажется ближе к М, чем к А.

Ответ: а) ; б) 1/2; в) 3/4.

 

1.2.33. Искусственный спутник Земли (ИСЗ) движется по орбите, которая заключена между 60° северной и 60° южной широты. Полагая падение ИСЗ в любую точку поверхности Земли между указанными параллелями равновозможным, найти вероятность того, что спутник упадет выше 30° северной широты.

Ответ 0,21.

 

1.2.34. Разведывательный приемник с постоянной скоростью и периодом T сканирует некоторый диапазон частот (f₁÷ f₂), где возможно появление сигнала, за которым установлено наблюдение. Полоса пропускания приемника равна 2Df. Наблюдаемый сигнал импульсный, его длительность << T, а ширина спектра <<(f₂÷ f₁), появление сигнала равновероятно в любой момент времени в любой точке интервала (f₁ - Df.,f₂ + Df).

Необходимо найти следующие характеристики:

а) вероятность Р ₁обнаружения сигнала;

б) вероятность Р ₂ пеленга местоположения передатчика, если частота сигнала известна, а антенна пеленгатора вращается равномерно, причем ширина диаграммы направленности антенны β =18º;

в) вероятность P ₃ обнаружения сигнала, если сигнал не является импульсным, а имеет конечную длительность t_и (считая, что регистрация сигнала приемником происходит мгновенно);

г) вероятность P ₄определения пеленга, если сигнал имеет длительность t_и, и за время t_и антенна пеленгатора поворачивается на угол 0,5 β.

Ответ: а) б) в) г)

 

1.2.35. На склад поступили три партии резисторов: две первые партии по 2000, а третья – 4000 штук. Брак в партиях составляет соответственно 1, 2 и 3%.

Каков ожидаемый процент брака в смешанной партии?

Ответ: 2,25%.

 

1.2.36. Методом случайной выборки проверяется партия изделий, содержащей a качественных изделий и b бракованных. Проверка первых т изделий (m<b) обнаружила, что все они бракованные.

Определить вероятность P того, что из следующих четырех проверяемых изделий по крайней мере два окажутся бракованными.

Ответ:

 

1.2.37. Из упаковки, содержащей n транзисторов, взят, по крайней мере, один транзистор.

Вычислить вероятность P того, что взято четное число транзисторов, если равновероятно извлечение любого числа транзисторов?

Ответ:

 

1.2.38. На вход устройства поступают двухсимвольные двоичные кодовые комбинации. Появление нуля и единицы равновероятно

Какова вероятность того, что в поступившей кодовой комбинации будет хотя бы один нуль?

Ответ: 3/4.

 

1.2.39. В упаковке содержится 36 транзисторов, среди которых 4 бракованных. Для проверки наугад выбирают 3 транзистора.

Какова вероятность того, что среди проверяемых транзисторов окажется хотя бы один бракованный.

Ответ: 0,305.

 

1.2.40. Два стрелка независимо один от другого стреляют по одному разу в цель. Вероятность попадания в цель для первого стрелка 0,8, а для второго – 0,9.

Какова вероятность попадания в цель хотя бы одной пули?

Ответ: 0,98.

 

1.2.41. Сигналы принимаются двумя независимыми приемниками. Вероятность приема первым приемником равна P₁ , вторым – Р₂.

Определить вероятность P приема сигналов хотя бы одним приемником.

Ответ: P =1- (1- P₁)(1- P₂).

 

1.2.42. Вероятность выхода частоты принимаемых колебаний за пределы полосы пропускания приемника из-за нестабильности несущей частоты передатчика равна 0,1, а из-за нестабильности частоты гетеродина приемника – 0,2.

Определить вероятность того, что частота принимаемых колебаний не выйдет за пределы полосы пропускания приемника.

Ответ: 0,72.

 

1.2.43. Две станции дальней радиосвязи одновременно ведут работу с одним корреспондентом на разных частотах. Вероятность прохождения радиосигналов на частоте f ₁ равна 0,7; вероятность прохождения на частоте f ₂ – 0,8.

Найти вероятность установления связи при одновременной работе обеих радиостанций.

Ответ: 0,94.

 

1.2.44. Вероятность вывода истребителя-перехватчика наземными системами наведения в район цели равна 0,8. Вероятность обнаружения цели бортовой радиолокационной станцией истребителя в этом районе равна 0,9. Вероятность уничтожения цели истребителем 0,75.

а) С какой вероятностью цель будет уничтожена?

Ответ: 0,54.

 

1.2.45. В студии три телевизионных камеры. Вероятность того, что каждая камера включена, равна 0,6.

Найти вероятность того, что в данный момент включена хотя бы одна камера.

Ответ: 0,936.

 

1.2.46. Вероятности попадания в цель при стрельбе из трех орудий соответственно равны: 0,8; 0,7; 0,9.

Вычислить вероятность хотя бы одного попадания при одном залпе из всех орудий.

Ответ: 0,994.

 

1.2.47. При изготовлении детали выполняются три операции. Вероятность брака на первой операции равна 0,01, на второй – 0,02 и на третьей – 0,025.

Определить вероятность изготовления стандартной детали при условии, что брак на отдельных операциях появляется независимо от других.

Ответ: 0,946.

 

1.2.48. При передаче текста 10% букв искажаются и принимаются неверно.

Какова вероятность того, что все пять букв некоторого слова будут приняты правильно?

Ответ: 0,59.

 

1.2.49. Цех в среднем выпускает 2% бракованных деталей. Из каждой сотни годных деталей в среднем 70 оказываются первого сорта.

Найти вероятность того, что деталь, изготовленная в цехе, окажется первого сорта.

Ответ: 0,686.

 

1.2.50. Вероятность попадания авиабомбы в цель равна 0,2. Найти вероятность поражения цели тремя бомбами, если 2% сброшенных бомб не взрываются.

Ответ: 0,48.

 

1.2.51. По каналу связи передаются пяти-символьные двоичные слова. Из-за помех они могут искажаться: каждый переданный символ искажается с вероятностью 0,01 и с вероятностью 0,99 принимается правильно. Все символы передаются и принимаются независимо друг от друга. Передана комбинация 10110.

а) Найти вероятность того, что она принята без искажений;

б) Найти вероятность того, что она будет принята как 11110;

в) Найти вероятность того, что в принятой комбинации будет искажен один символ.

Ответ: а) 0,99⁵, б) 0,0,01*0,99⁴; в) 0,05*0,99⁴.

 

1.2.52. Цепь подсвета приборной доски состоит из 8 последовательно включенных лампочек. Вероятность того, что каждая из них будет исправна в течение 1000 ч, равна 0,9.

Чему равна вероятность P того, что цепь не выйдет из строя за этот промежуток времени?

Ответ: P = 0,430.

 

1.2.53. Устройство содержит n 1микросхем, n 2 транзисторов и п 3предохранителей. Выход любой детали из строя приводит к неисправности устройства. Вероятность выхода из строя за время T одной микросхемы q ₁,транзистора q ₂, предохранителя q ₃.

Найти вероятность Q того, что за время T устройство выйдет из строя?

Ответ:

 

1.2.54. Линия связи содержит цепочку из m ретрансляторов. Надежность (вероятность безотказной работы) каждого ретранслятора одинакова. Ретрансляторы выходят из строя независимо друг от друга, причем отказ любого ретранслятора влечет за собой отказ линии связи.

Определить требуемую вероятность p₁ безотказной работы каждого ретранслятора за промежуток времени T, если надежность всей линии связи за этот промежуток времени должна быть не менее P.

Ответ:

 

1.2.55. Шкала устройства освещается четырьмя параллельно включенными лампочками. Вероятность того, что каждая из лампочек будет исправна в течение 1500 ч, равна 0,9.

Какова вероятность того, что шкала будет освещена в течение этих 1500 ч, если вышедшие за это время из строя лампочки не заменяются исправными?

Ответ: 0,9999.

 

1.2.56. Электрическая цепь (рис. 1.6) состоит из n последовательныхгрупп нагревательных элементов, каждая из которых содержит k параллельных ветвей. Вероятность перегорания за время T одного элемента ветви равна q.

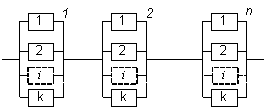
Рис. 1.6

Найти вероятность P того, что в течение интервала времени T ток в цепи будет отличен от нуля.

Ответ: P = (1-q ^k)ⁿ.

 

1.2.57. Радиоэлектронный блок состоит из трех параллельных цепей, каждая из которых включает в себя четыре последовательно соединенных элемента. Две цепи являются резервными. Надежность элементов в основной цепи 0,97, в резервных цепях 0,92.

Определить надежность блока.

Ответ: 0,991.

 

1.2.58. Разрыв электрической цепи может произойти вследствие выхода из строя элемента k или двух элементов k₁ и k₂. Вероятность выхода из строя элемента k равна q_k = 0,3, а для элементов k₁ и k₂ равна q₁ = q₂ = 0,2.

Определить вероятность разрыва электрической цепи.

Ответ: 0,328.

 

1.2.59. Система состоит из пяти элементов; надежность p каждого элемента равна 0,8. Работа каждого элемента необходима для работы системы в целом. Для повышения надежности системы предлагается три варианта соединения элементов (рис. 1.7а, 1.7б, 1.7в).

Какой вариант резервирования наиболее надежный?