Условие и уравнения равновесия произвольной плоской системы сил.

Аксиомы статики

Статика- раздел механики, который изучает условия равновесия твердых тел под влиянием приложенных к ним сил.

Аксиомы статики:

1) Принцип инерции. Под действием уравновешенной системы сил, абсолютно твердое тело или
материальная точка находятся в равновесии или движутся равномерно и прямолинейно.
2) Условия равновесия сил. Две силы равные по модулю и направленные по одной прямой в разные стороны уравновешиваются. |F₁|=|F₂|
3) Принцип присоединения. Не нарушая механического состояния тела к нему можно добавить или убрать уравновешенную систему сил. |F₁|=|F₂|; |F₃|=|F₄|.

Следствие из 2 и 3 аксиом. Силу действующую на твердое тело можно перемещать вдоль линии её действия.

4) Правила параллелограмма. Равнодействующая двух сил, приложенных в одной точке, приложена в этой же точкеи является диагональю параллелограмма построенного на этих силах, как на сторонах. |F₁|=|F₂|=|F₃|;

F₀ →+ (F₂; А₃)

- (F₁; F₂)

 

5) Закон действия и противодействия. При взаимодействии материальных тел всякому действию есть равное и противоположно направленное противодействие. |F₁|=|F₂|

Связи и реакции связей

 

Все тела делятся на: свободные (перемещение не ограничено)

и связанные (перемещение которых ограничено другими телами(связи))

 

Силы, действующие от связей и препятствующие перемещению, называют реакциями связей.

Принцип освобождения от связи. Всякое связанное тело можно представить свободным, если связи заменить их реакциями.

Типы связи:

1) В вид жесткого прямого стержня сшарнирным закреплением концов.

[R]- реакция.

Реакции, направленные вдоль стержня, могут быть растянутыми или сжатыми.

2) Связь, осуществляемая ребром двугранного угла и точечной опоры.

3) Гибкая связь (веревка, трос, цепь).

4) Связь в виде гладкой плоскости.

5) В виде шероховатой плоскости.

Проекция силы на ось.

Проекция силы на ось равна произведению модуля этой силы на косинус угла между силой и положительным направлением оси.

Условия равновесия плоской системы сходящихся сил: геометрическая и аналитическая форма.

Условия и уравнения плоской системы сходящихся сил.

Плоская система сил будет находиться в равновесии, если их равнодействующая будет равна 0 (F_∑=0)

Формула равн. необходимо и достаточно, чтобы силовой многоугольник, построенный для данной системы сил, был замкнутый.

Аналитическая форма имеет два уравнения равновесия: (1 Е F_x=0) (E F_y =0). Алгебраическая сумма проекции всех сил на ось иксов должна быть равна нулю и на ось игрик тоже должна быть равна нулю.

Плечо и момент силы относительно точки, правило знаков.

Теорема Пуансо о параллельном переносе сил. Не изменяя действия силы на тело, её можно перенести параллельно по своему начальному направлению в любую точку тела, присоединяя при этом некоторую пару. |F|=|F’|=|F”|.

F’

(F, F”)

Главный момент данной плоской системы сил- это сумма моментов всех сил относительно какой-либо точки о. (М гл.)

М гл.=∑М₀ (F)

6.Плечо и момент силы относительно оси, правило знаков
плече - кротчайшее расстояние между линиями сил.момент силы наз вращательное усилие создаваемое вектором силы относительно другого объекта. момент пары сил будет считаться положительным если пара стремится сообщить ему вращательное движение по часовой стрелке,если против будет считаться отрицательным.
8 вопрос: статическая- не меняется со временем или меняется очень медленно
динамическая- меняется значение в короткий промежуток времени вызывает большие силы инерции может привести к внезапному разрушению
повторно переменные - многократно меняет значение и знаки

Условие и уравнения равновесия произвольной плоской системы сил.

это сис-ма,когда линии действия сил лежат в одной плоскости и расположены в прои звольном порядке.
теорема пуансо: не изменяя действия силы на тело,её можно переместить параллельно своему начальному направлению в любую точку тела, присоединяя при этом некоторую пару

8. Классификация нагрузок.
статическая- не меняется со временем или меняется очень медленно
динамическая- меняется значение в короткий промежуток времени вызывает большие силы инерции может привести к внезапному разрушению
повторно переменные - многократно меняет значение и знаки

9.Опорные устройства балочных систем.
шарнирно- подвижная опора
шарнирно - неподвижная опора
жестко - защемленная опора

10.Пространственная система сходящихся сил. Условия и уравнения равновесия.
пространственная сис- ма сходящихся сил: линии действия сил пересекаются в одной точке,но не лежат в одной плоскости.
условия равновесия в аналитической форме:
1 Fx= 0
2 Fy=0
3 Fz=0
геометр. форма: необходимо и достаточно,чтобы силовой многоугольник,построенный для этой сис-мы сил был замкнутым.

11.Момент силы относительно оси.
Момент силы относительно оси равен моменту проекции этой силы на плоскость перпендикулярной данной оси относительно точки пересечения оси с плоскостью.
Знак определяется с помощью положительного направления оси, если по часовой стрелке то -, если по часовой стрелке то +.
Следствие:
1. Момент не изменяется при переносе силы вдоль линии её действия.
2. Момент силы относительно оси равен 0 если сила и ось лежат в одной плоскости.

12.Условия равновесия системы сил произвольно расположенных в пространстве.
Условия равновесия:
Для равновесия произвольной плоской системы необходимо и достаточно, чтобы сумма моментов относительно двух произвольно взятых точек тела была равна нулю и сумма проекций сил на одну из осей коpординат была равна нулю.

аналитическая форма равновесия:
1.Fx = 0 4. Mx(F) = 0
2.Fy = 0 5. My(F) = 0
3.Fz = 0 6. M2(F) = 0

13.Положение центра тяжести простых геометрических фигур.

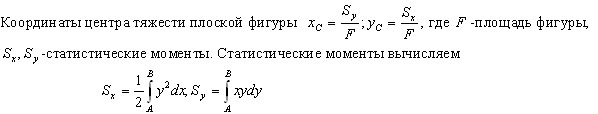
Точка приложения силы тяжести:
Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей:

Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси.

14. Виды движений в зависимости от ускорений.
Различают следующие виды движения точки в зависимости от ускорения:
1. Прямолинейное движение. В этом случае траектория движения точки – прямая, причем точка движется вдоль этой прямой в одном направлении. Радиус кривизны прямой R равен бесконечности (прямую можно считать окружностью бесконечно большого радиуса).
2. Равномерное криволинейное движение. Так как при равномерном движении точки модуль скорости остается постоянным, то есть v = const
3. Равномерное прямолинейное движение
4. Равнопеременное криволинейное движение. Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время величиной постоянной

15. Линейные скорости и ускорения точек вращающегося тела.
Если тело вращается вокруг оси, то его точки перемещаются по окружностям, радиусы которых r равны расстояниям точек от оси вращения.
Касательное и нормальное ускорения при вращательном движении твердого тела также называют соответственно вращательным и центростремительным.
- Касательное ускорение точки вращающегося тела определяется из выражения

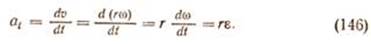
- Нормальное ускорение точки равно отношению квадрата ско­рости к радиусу окружности

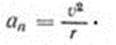
Значение полного ускорения вычисляется как диагональ пря­моугольника, построенного на составляющих ускорениях At, и An. Подставив значения касательного и нормального ускорений, получим

 

Аксиомы динамики.

Первая аксиома (принцип инерции):
- Всякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния
Вторая аксиома (второй закон Ньютона — основной закон динамики):
- Ускорение, сообщенное материальной точке силой, пропорционально величине силы и совпадает с направлением силы.
Зависимость между силой, действующей на материальную точку, и сообщаемым ею ускорением следующая:

·F = ma,

·где m —масса точки, кг; а — ускорение точки, м/с2
Третья аксиома (третий закон Ньютона):
- Силы взаимодействия двух тел равны по величине и направлены по одной прямой в разные стороны.
Четвертая аксиома (закон независимости действия сил):
- Ускорение, сообщаемое точке системой сил, равно геометрической сумме ускорений, сообщенных точке каждой силой в отдельности.

17. Принцип Даламбера.
Принцип Даламбера: материальная точка под действием активных сил, реакции связей и условно приложенной силы инерции находится в равновесии.
F + R + Fин = 0; F- активная сила, R - сила реакции; Fин - сила инерции.

18.

19. Понятие о мощности.
Мощностью называется работа, совершаемая силой в единицу времени.
Pcp = ΔW / Δt - мощность при вращении; F Δs cos a / Δt - мощн. при поступательном движении.
Pcp - средняя мощность; F - cилы; Δt - время;Δs - перемещение.
За единицу мощности принят ватт (Вт) - мощность соответсвующая работе в один джоуль в секунду.

20. Моменты инерции однородных тел.
Момент инерции массы любого тела:
J= m · r²
[ j ] = [m] [r²] = кг*м²
1. Для однородного стержня относительно оси, перпендикулярной к оси стержня и проходящей через его конец:
Jz = ml²\3
где, m – масса стержня, l – длинна стержня.
2. Для однородного цилиндра:
Jz = mD²\8
где, m – масса цилиндра, D –диаметр цилиндра.
3. Для окружности или тонкого кольца, если пренебречь его толщиной:
Jz = mD²\4

21. Классификация элементов конструкций
1.Брус-тело у которого длина значительно больше других размеров.
2.Пластина(оболочка)-тело у которого толщина значительно меньше других размеров.
3.Массивное тело(массив)три размера одного порядка

22.Метод сечения и его применение
Заключается в мысленном рассечении тела плоскостью, отбрасывании одной из частей, в рассмотрении в равновесии отсеченной части, составлении уравнений равновесия из которых необходимо определить значение и знак внутренних силовых факторов

23.Закон Гука.
Основной закон в сопромате.
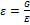,G= 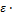E. E-модуль продольной упругости(величина которая характеризует жесткость материала).
Продольная деформация прямопропорциональна соответствующему нормальному напряжению, т.е. способность сопротивляться упругому деформированию.

24. Расчет на прочность при растяжении.
· проверочные
Условие прочности при растяжении и сжатии.
·проектировочные:
-определение размеров поперечного сечения ,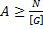
-подбор материалов 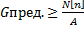, 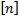-требуемый коэффициент запаса прочности.

· Определение нагрузочной способности
, A- площадь поперечного сечения

25.Срез и смятие. Условие прочности.
Срез-разрушение материала, под воздействием касательных напряжений.
Условия прочности при срезе.
. -допускаемое напряжение, Q-поперечная сила,
Q=F, - расчетное касательное напряжение, А-площадь среза.
Смятие- местная деформация сжатия по площадкам передачи давления.
Условие прочности элементов работающих на смятие.
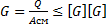-допускаемое норм. Напряжение
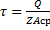, Z-кол-во заклепок
Q=F. Площадки передачи давления Aсм=d· 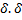-толщина листа

26. Кручение. Условия жёсткости и прочности при кручении.
Кручением называется такой вид нагружения (деформации), при котором в поперечных сечениях бруса возникает только один внутренний силовой фактор – крутящий момент. Этот вид нагружения возникает при приложении к брусу пар сил, плоскости действия которых перпендикулярны его оси.

Условия прочности и жесткости вала
Расчет вала при кручении сводится к одновременному удовлетворению двух условий:
- условия прочности:

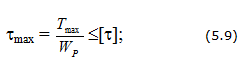
- условия жесткости:

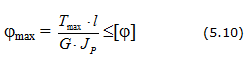
Вопрос27

Изгиб — вид деформации, при котором происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев. Изгиб связан с возникновением в поперечных сечениях бруса изгибающих моментов.
Чистый изгиб – такой вид нагружения, при котором в поперечных сечениях бруса возникают только изгибающие моменты.
Брус, работающий при изгибе, называется балкой. Конструкция, состоящая из нескольких изгибаемых стержней, соединенных между собой чаще всего под углом 90, называется рамой.
Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения
Если изгибающий момент является единственным внутренним силовым фактором, то такой изгиб называется чистым. При наличии поперечной силы 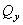изгиб называется поперечным.
Косой изгиб - изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции.
Сложный изгиб - изгиб, при котором нагрузки действуют в различных (произвольных) плоскостях.
Если внешняя сила вращает отрезанную часть балки по часовой стрелке, то сила является положительной, если внешняя сила вращает отрезанную часть балки против хода часовой стрелки, то сила является отрицательной.

28. Пониятие о механических передачах, их классификация
Механическая передача — механизм, служащий для передачи и преобразования механической энергии от энергетической машины до исполнительного механизма(органа) одного или более, как правило с изменением характера движения (изменения направления, сил, моментов и скоростей). Как правило, используется передача вращательного движения.

Классификация
Передачи зацепления:

• Цилиндрические зубчатые передачи:
  
  - Прямозубые цилиндрические передачи
  - Косозубчатые цилиндрические передачи
  - Шевронные цилиндрические передачи обладают крайне высокой плавностью работы.
• Конические зубчатые передачи в отличие от цилиндрических имеют пересекающиеся оси входных и выходных валов. Применяются если необходимо изменить направление кинетической передачи.
  - червячные
  - цепные;
  - зубчатыми ремнями;
  - винтовые.

• Передачи трения:
  - фрикционные;
  - ремённые.
• Зубчатые передачи с магнитным взаимодействием.

• Способ соединения ведущего и ведомого звена:
  - непосредственный контакт (зубчатые, фрикционные, винтовые, червячные);
  - с гибкой дополнительной связью (ремённые, цепные).

• По управляемости делятся на:
  - с фиксированным передаточным числом
  - со ступенчато изменяемым передаточным числом (коробка передач)
  - с плавно изменяемым передаточным числом (вариатор)
  
  
  Вопрос 29
• Фрикционная передача — кинематическая пара, использующая силу трения для передачи механической энергии.
  
  Классификация
  Фрикционные передачи делятся на передачи:
  - с параллельными валами
  - с пересекающимися валами
  - с внешним контактом
  - с внутренним контактом
  
  По возможности варьирования передаточного отношения
  - нерегулируемые (i=const)
  - регулируемые (фрикционный вариатор)
  
  По возможности изменения передаточного отношения при наличии промежуточных тел в передаче по форме контактирующих тел:
  - цилиндрические
  - конические
  - сферические
  - плоские
• Достоинства фрикционных передач:
  - простота конструкции и обслуживания;
  - плавность передачи движения и регулирования скорости и бесшумность работы;
  - большие кинематические возможности (преобразование вращатель­ного движения в поступательное, бесступенчатое изменение скоро­сти, возможность реверсирования на ходу, включение и выключение передачи на ходу без остановки);
  - за счет возможностей пробуксовки передача обладает предохрани­тельными свойствами. Однако после пробуксовки передача, как пра­вило, резко ухудшает свои качества - появляются лыски на катках, неравномерно срабатываются фрикционные поверхности и т.д. По­этому использовать пробуксовку как предохранительное средство не рекомендуется;
  - отсутствие мёртвого хода при реверсе передачи;
  - равномерность вращения, что удобно для приборов;
  - возможность бесступенчатого регулирования передаточного числа, причем на ходу, без остановки передачи.
• Недостатки фрикционных передач:
  - непостоянство передаточного числа из-за проскальзывания;
  - незначительная передаваемая мощность (открытые передачи - до 10-20 кВт; закрытые - до 200-300 кВт);
  - для открытых передач сравнительно низкий КПД;
  - большое и неравномерное изнашивание катков при буксовании;
  - необходимость применения опор валов специальной конструкции с прижимными устройствами (это делает передачу громоздкой);
  - большие нагрузки на валы и подшипники от прижимной силы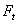 , что увеличивает их размеры и делает передачу громоздкой. Этот недостаток ограничивает величину передаваемой мощности;
  - для силовых открытых передач незначительная окружная скорость (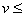 7 - 10 м/с);
  - большие потери на трение.

Применение.
Фрикционные передачи с нерегулируемым передаточным числом в машиностроении применяются сравнительно редко, например, во фрикционных прессах, молотах, лебедках, буровой технике и т.п.). В качестве силовых передач они громоздки и малонадежны. Эти передачи применяются преимущественно в приборах, где требуется плавность и бесшумность работы (магнитофоны, проигрыва­тели, спидометры и..)

п.). Они уступают зубчатым передачам в несущей способности. Зато фрикционные передачи с бесступенчатым регулированием скорости – вариаторы – широко применяются в различных машинах, например, в металлорежущих станках, в текстильных и транспортирующих машинах и т. д. Зубчатые передачи не позволяют такого регулирования. На практике широко применяют реверсивные фрикционные передачи винтовых прессов, передачи колесо — рельс и колесо — дорожное полотно самоходного транспорта. Фрикционные передачи предназначены для мощностей, не превышающих 20 кВт, окружная скорость катков допускается до 25 м/с.

 

Вопрос 30

Зубчатая переда́ча — Механизм, в котором два подвижных звена являются зубчатыми ко­лесами, образующими с неподвижным звеном вращательную или поступатель­ную пару, называют зубчатой передачей

Классификация