Лабораторная работа 7
расчет Нагрева тел правильной формы
Цель работы
Численное исследование нагрева тел правильной формы различной геометрии. Сравнение и анализ расчетных результатов, полученных при разной размерности задачи.
Основы теории и расчетные формулы
Процесс теплопроводности называется нестационарным, если поле температуры в объеме тела изменяется во времени.
Аналитическое описание процесса изменения температуры во времени в каждой точке тела можно получить путем решения дифференциального уравнения теплопроводности с определенными краевыми условиями.
Нелинейное дифференциальное уравнение теплопроводности при отсутствии внутренних источников теплоты имеет вид:
, (7.1)
где 
– температура тела, К, в точке 
в момент 
;
– плотность вещества, кг/м3;
– удельная теплоемкость вещества, Дж/(кг × К);
– коэффициент теплопроводности вещества, Вт/(м× К);
– расчетная область пространства, в пределах которой решается уравнение теплопроводности, отделенная от окружающей среды граничной поверхностью 
.
Если можно считать коэффициент теплопроводности 
не зависящим от температуры, то его можно вынести за знак дивергенции. Тогда, разделив обе части уравнения на (
), получим линейное уравнение теплопроводности:
, 
, (7.2)
где 
– коэффициент температуропроводности, м 2/ с;
– оператор Лапласа, имеющий следующий вид:
Коэффициент температуропроводности характеризует термоинерционные свойства материала – чем он больше, тем быстрее происходит перестройка температурного поля в теле при стремлении его к равновесному состоянию.
Чтобы решить задачу теплопроводности, т.е. найти распределение температуры в теле и его изменение во времени , необходимо не только знать конкретную форму уравнения теплопроводности для данного случая (линейное или нелинейное, одно-, двух-, или трехмерное), но и знать условия однозначности.
Только задав условия однозначности, можно получить единственное решение, соответствующее конкретным условиям нагрева (охлаждения).
В условия однозначности входят:
- геометрические условия (определяющие форму и размеры расчетной области 
и ее поверхности 
) и физические параметры материала (
), задаваемые при формулировке уравнения теплопроводности;
- краевые условия, включающие в себя, в свою очередь,
а) начальные условия, т.е. распределение температуры в объеме тела в некоторый момент времени, принимаемый за начало отсчета;
б) граничные условия, характеризующие тепловое взаимодействие окружающей среды с поверхностью тела.
В простейшем случае рассматривают однородные начальные условия, при которых в нулевой момент времени температура тела в любой его точке равна одному и тому же значению 
:, 
, (7.3)
Граничные условия могут быть заданы тремя различными способами:
1. Граничные условия первого рода (первая краевая задача). В этом случае задается распределение температуры по всей поверхности тела и изменение этого распределения во времени,т.е. задается функция
, (7.4)
где индекс " 
" соответствует поверхности тела.
В частном случае эта температура может быть постоянной во времени, а кроме того, и неизменной по всей поверхности тела.
2. Граничные условия второго рода (вторая краевая задача). В этом случае задается распределение плотности теплового потока по всей поверхности тела и изменение этого распределения во времени. С учетом постулата Фурье 
граничные условия второго рода можно записать следующим образом:
(7.5)
где 
– координата, направленная по нормали к поверхности тела.
В частном случае плотность теплового потока на поверхности тела может быть постоянной во времени, а кроме того, и неизменной по всей поверхности тела.
3. Граничные условия третьего рода (смешанная краевая задача). В этом случае задается температура окружающей среды 
и закон теплообмена между средой и поверхностью тела.
Граничные условия третьего рода являются наиболее общими и наиболее часто встречающимися на практике. По существу, в этом случае задается некоторая связь между величиной плотности теплового потока на поверхности тела и температурой его поверхности. Если внешний теплообмен между окружающей средой, имеющей температуру 
, и поверхностью тела с температурой 
происходит путем конвекции, то справедлива формула Ньютона–Рихмана:
,
и с учетом постулата Фурье математическая формулировка граничных условий третьего рода принимает вид:
(7.6)
Иногда формулу Ньютона–Рихмана применяют даже в ситуациях, когда одним из механизмов теплообмена является излучение; в этом случае 
– суммарный коэффициент теплоотдачи, Вт/(м2 × К),
Таким образом, линейные граничные условия третьего рода формулируются в виде уравнения, в котором известными величинами являются коэффициент теплоотдачи , температура среды и коэффициент теплопроводности тела . Как температура поверхности тела, так и плотность теплового потока на поверхности остаются при этом неизвестными функциями времени и координат.
Дифференциальное уравнение теплопроводности (7.2) совместно с начальными условиями (7.3), а также граничными условиями (7.4), (7.5) или (7.6) дает законченную математическую формулировку рассматриваемой задачи. Решение этой задачи заключается в отыскании такой функции:
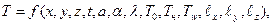
(где 
– характерные размеры тела), которая удовлетворяла бы уравнению (7.2) и одному из условий (7.4), (7.5) или (7.6).
Задачи нестационарной теплопроводности могут решаться различными аналитическими методами (метод разделения переменных, операционные методы), методами аналогий (электроаналогии и гидроаналогии), а также численными методами.
В данной работе ограничимся рассмотрением задач с граничными условиями третьего рода, причем только тех из них, которые могут быть решены аналитически. Прежде всего – это одномерные задачи, которые могут возникнуть при различной геометрии расчетной области в случае симметричных и однородных граничных условиях.
Если тело имеет форму параллелепипеда, один из размеров которого (толщина) мал по сравнению с двумя остальными, и вдоль этих двух остальных направлений граничные условия однородны, то в таком теле температурное поле будет изменяться только по толщине. Такое тело называют (полу) бесконечной пластиной. Аналогичным образом, если тело имеет форму цилиндра, длина которого велика по сравнению с диаметром, и вдоль оси цилиндра (а также по угловой координате) граничные условия распределены однородно, то в таком теле, называемом (полу) бесконечным цилиндром, температурное поле будет изменяться только по радиальной координате. Аналогичная ситуация возникает с шаром, который нагревается при симметричных (однородных) граничных условиях.
Для постановки и решения задачи методом разделения переменных бывает удобно перейти от обычной температуры к избыточной температуре 
. В таблице 7.1 представлены постановки одномерных задач теплопроводности для тел различной формы, сформулированные относительно избыточной температуры, а также их решения, полученные методом разделения переменных.
Как видно из представленных в таблице 7.1 данных, решение нестационарной задачи теплопроводности представляет собой сумму членов бесконечного ряда, содержащего корни трансцендентного уравнения, получаемого из граничных условий на поверхности теплообмена. Для пластины и шара ряд основан на тригонометрических функциях, а для цилиндра – на функциях Бесселя первого рода нулевого (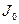
) и первого (
) порядка.
Из структуры характеристического уравнения видно, что его корни зависят только от параметра 
. Эта безразмерная величина 
, называемая критерием Био, характеризует отношение интенсивностей внешнего и внутреннего теплообмена; она содержит характерный размер 
, который равен полутолщине d для пластины (при симметричном нагреве) и радиусу 
для цилиндра и шара. Решение задачи теплопроводности можно представить в безразмерном виде
, (7.7)
где 
– безразмерная избыточная температура;
(или 
) – безразмерная координата, которая изменяется в интервале [0,1];
– критерий Фурье, представляющий собой безразмерное время.
Таким образом, безразмерная избыточная температура зависит от безразмерной координаты 
, безразмерного времени 
и единственного безразмерного параметра .
Решения (7.7) для тел различной геометрической формы могут быть представлены в виде номограмм, которые предложены инженером-металлургом Будриным Д.В. еще в первой половине XX века и с тех пор широко используются в инженерной практике. Эти номограммы представляют собой зависимость относительной избыточной температуры 
от безразмерного времени при фиксированном значении безразмерной координаты (чаще всего – для центра или поверхности тела, т.е. для 
или 
). Область графика содержит семейство кривых, каждая из которых соответствует определенному значению критерия .
| Пластина | Цилиндр | Шар | |
| Уравнение теплопроводности | 
| 
| 
|
| Начальное условие | при = 0 0   ;
| при = 0 0   ;
| при = 0 0 ;
|
| Граничное условие на поверхности теплообмена | 
| 
|
|
| Граничное условие на поверхности симметрии | 
| 
|
|
| Общий вид решения | 
| 
| 
|
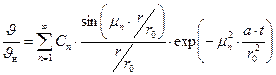
Значение коэффициента 
| 
| 
| 
|
| Вид трансцедентного уравнения для m | 
| 
| 
|
Таблица 7.1 – Постановка и вид решения одномерных задач теплопроводности с г.у. 3 рода для тел различной правильной формы
Пользуясь номограммами, можно найти решение дифференциального уравнения теплопроводности – определить температуру какой-либо точки тела в заданный момент времени. С помощью этих же номограмм можно решить задачу в обратной постановке: определить время нагрева тела до заданной температуры.
При наличии номограмм расчет нагрева (охлаждения) тел при нестационарном режиме сводится к вычислению критериев и (прямая постановка задачи), либо и 
(обратная постановка задачи), и последующему нахождению неизвестной величины по номограммам.
Многолетняя практика применения номограмм Будрина Д.В. выявила не только их огромную роль в теплотехнических расчетах, но и определенные ограничения:
а) всегда существует погрешность применения графической информации, и в некоторых случаях она может оказаться сопоставимой с теми эффектами, которые исследователь пытается выявить расчетным путем;
б) погрешность усугубляется неизбежными погрешностями интерполяции пользователем, поскольку вдоль оси ординат график построен в логарифмических координатах;
в) при малых числах Фурье кривые, построенные для разных чисел Bi, сильно сгущаются, что создает значительную погрешность при их использовании;
г) обычные номограммы построены для регулярного режима (т.е. при Fo >0,3), поэтому при малых числах Фурье необходимо использовать другие номограммы, что не очень удобно.
В связи с изложенным выше на современном этапе развития вычислительной техники целесообразно для инженерных расчетов пользоваться компьютерными вычислениями решения задачи теплопроводности, которые свободны от перечисленных недостатков и позволяют брать при суммировании такое количество членов ряда, которое необходимо для получения требуемой точности.
Что касается обратной постановки задачи, то она тоже доступна для компьютерного варианта расчета, но для нее необходимо использовать численные методы, связанные с поиском решения нелинейного уравнения. Задача сводится к решению уравнения
, (7.8)
где функция от безразмерного времени
(7.9)
задана неявно (здесь 
– заданное значение относительной избыточной температуры, а – одна из функций, являющихся решением соответствующей задачи теплопроводности (таблица 7.1). Неявный характер задания 
делает возможным для решения уравнения только два метода – метод простой итерации и метод половинного деления; второй из них представляется более предпочтительным, т.к. обладает абсолютной надежностью (не может разойтись при правильно заданном отрезке поиска).
На первый взгляд, знание решений одномерных задач (кроме задачи для шара) имеет чисто академический характер, т.к. реальные тела всегда имеют конечные размеры. Однако это не совсем так по двум причинам: а) в ряде случаях заготовки характеризуются такими размерами и нагреваются в таких условиях, когда допущение о независимости температурного поля от той или иной координаты абсолютно правомерно; б) знание решения одномерных задач теплопроводности при определенных условиях позволяет получить решение многомерных задач.
Если рассматриваемое тело представляет собой геометрическое место точек пересечения полубесконечных тел, и это тело нагревается при однородных (одинаковых со всех сторон) граничных условиях, то решение задачи теплопроводности для этого тела равно произведению решений для полубесконечных тел, пересечением которых оно является.
Это утверждение, называемое принципом суперпозиции, позволяет получить решение для параллелепипеда конечных размеров и цилиндра конечной длины, пользуясь решениями для соответствующих одномерных задач.
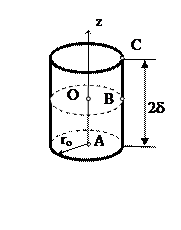
а б
Рисунок 7.1 – параллелепипед (а) и цилиндр конечной длины (б)
Так, например, параллелепипед, изображенный на рис.7.1, а, может быть представлен, как область пересечения трех пластин толщинами, соответственно, 2dx, 2dy,2dz.. Тогда для точек O, A,B,C (центр заготовки, центр грани, центр ребра и угол) справедливы следующие соотношения (верхний индекс обозначает центр или поверхность пластины, а нижний – направление, в котором эта пластина имеет конечный размер)
; 
; 
; 
(7.10)
Аналогично, цилиндр конечной длины можно представить, как пересечение цилиндра бесконечной длины и полубесконечной пластины. Тогда для точек, отмеченных на рис.7.1, б, применимы следующие соотношения (верхний индекс обозначает центр или поверхность полубесконечного тела, а нижний – его геометрию)
; 
; 
; 
.. (7.11)
Конечно, применять принцип суперпозиции и получать решения многомерных задач можно и при использовании номограмм – если речь идет о прямых задачах теплопроводности. А вот если понадобится решать обратную задачу для параллелепипеда или цилиндра конечной высоты, то применение номограмм невозможно, поскольку для каждой из подзадач (описывающих полубесконечное тело) должно быть свое число Фурье. Подход же, основанный на решении уравнения вида (7.8), вполне применим и для многомерных задач, но только следует в качестве аргумента рассматривать не число Фурье, а время от начала процесса нагрева. Тогда, например, для центра параллелепипеда должно решаться уравнение вида
, (7.12)
в левой части которого стоит функция только одного аргумента – времени t.
Решение этой задачи целесообразно проводить тем же методом, что и в одномерном случае – методом половинного деления.
Алгоритм этого метода применительно к данной конкретной задаче выглядит следующим образом:
1.Вычисление (в приближении регулярного режима, когда каждый ряд заменяется его первым членом) значения времени, соответствующего заданной температуре в расчетной точке t0 (логарифмированием).
2.С шагом Dt=0,01×t0, откладываемым влево и вправо от t0, нахождение таких значений tmin и tmax, в которых функция вида (7.12) имеет разные знаки (т.е.F min× F max<0)
3. Нахождение середины отрезка и вычисление значения функции в ней:
t=(tmin + tmax)/2, Ft=F(t)
4. Если F min× F t >0, то tmin =t; F min= F t, а иначе tmax=t; F max= Ft
5.Если |F max – F min| > Dдоп, возврат к п.3;
6.Вычисление окончательного решения t=(tmin + tmax)/2.