· сформировать навык применения знаний о разветвляющихся алгоритмах и логических высказываниях для решения задач с помощью электронных таблиц Excel;
· развить умения применять логические функции И, ИЛИ, НЕ, ЕСЛИ для решения задач с помощью электронных таблиц Excel;
· развить навык построения диаграмм и создания блок-схем в электронных таблицах Excel;
· способствовать развитию творческого подхода и логического мышления;
· воспитывать самостоятельность и трудолюбие.
· 3. Изложение нового материала:
· В электронных таблицах Excel для составления логических высказываний используют функции из категории “Логические”: И(); ИЛИ(); НЕ(); ИСТИНА(); ЛОЖЬ().
· Логические высказывания используются в разветвляющихся алгоритмах при проверке условия. Если логическое выражение истинно, то алгоритм пойдет по одной ветке, если ложно, то по другой. В электронных таблицах Excel для проверки условия используют функцию из категории “Логические”: ЕСЛИ (<условие в виде логического высказывания>; <действие в случае истинности высказывания>;<действие в случае ложности высказывания>). Для определения количества совпадений по заданному условию используют функцию из категории “Статистические”: СЧЁТЕСЛИ (<диапазон>; <условие>). Рассмотрим применение этих функций на примерах.
· Пример 1: Определить, принадлежит ли точка с координатами (x,y) выделенной области (см. Рисунок 1).
· 
· Рисунок 1
· На рисунке видно, что область состоит из двух частей С и D. Каждая область в свою очередь является пересечением плоскостей (множество точек, удовлетворяющих неравенству). Для определения этих плоскостей составим неравенства, которые получаются из уравнений прямых и окружности, ограничивающие эти плоскости. Для решения задачи определим выделенную область как объединение (дизъюнкция) областей С и D. В свою очередь область C определим как пересечение плоскостей (конъюнкция): (y<0), (x<0) и (x^2+y^2<4), а D – как пересечение плоскостей: (x^2+y^2>4) и ((0<x) и (x<2) и (-2<y) и (y<0)). Тогда условие для проверки принадлежности точки выделенной области запишется так: (y<0) & (x<0) & (x^2+y^2<4) + (x^2+y^2>4) & ((0<x) & (x<2) & (-2<y) & (y<0)) или, используя логические функции и относительные ссылки на ячейки А2 и В2 (где хранятся значения координат (х, у) заданной точки) ИЛИ (И(B2<0; A2<0; A2^2 + B2^2 < 4); И(A2^2+B2^2>4; 0<A2; A2<2; -2<B2; B2<0)). Это условие подставим в ячейку С2 в функцию ЕСЛИ(). И для набора точек скопируем эту формулу на следующие ячейки С3-С11. Получим следующий результат (см. Таблицу 3):
· Таблица 3
| x | y | D0 |
| -1 | не принадлежит | |
| не принадлежит | ||
| -1 | не принадлежит | |
| -1,8 | принадлежит | |
| -1,7 | 1,7 | не принадлежит |
| не принадлежит | ||
| -1,2 | не принадлежит | |
| -0,5 | 0,5 | принадлежит |
| не принадлежит | ||
| 1,5 | 1,5 | не принадлежит |
· Для наглядности на другом листе вставим диаграмму, изображающую эту область. С помощью мастера диаграмм выберем точечную диаграмму со значениями, соединенными отрезками без маркеров. Для нее подготовим таблицу точек. Для окружности используем полярные координаты, которые зависят от угла F и радиуса R: x=R*cos(F), y=R*sin(F). В нашем примере R=2, а угол F меняется от 0 до 2*ПИ(). Для квадрата достаточно указать координаты вершин в порядке обхода. Получим (см. Рисунок 2):
· 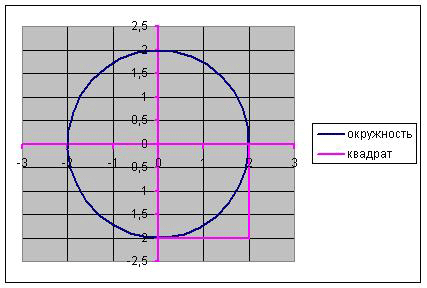
· Рисунок 2
· Пример 2: Определить наибольший общий делитель двух чисел m и n по алгоритму Евклида.
· Приведем блок-схему алгоритма Евклида (см. Рисунок 3):
· 
· Рисунок 3
· Пусть значения m и n находятся в ячейках A2 и B2, а результат – в ячейке C2, в которой и будет записана формула. В алгоритме используется два условия, поэтому функция ЕСЛИ будет вызвана дважды: =ЕСЛИ (A2=B2; B2; ЕСЛИ (A2>B2; A2-B2; B2-A2)). Так как значения переменных тоже меняются, то вставим функцию ЕСЛИ ниже в ячейки A3 (=ЕСЛИ (A2>B2; A2-B2; A2) и B3 (=ЕСЛИ (A2<B2; B2; B2-A2). Теперь скопируем формулы ниже до тех пор, пока значения не станут равными. Получим следующий результат (см. Таблицу 4):
· Таблица 4
| m | n | НОД (m, n) |
· 4. Практическая работа на компьютере:
· Задание для самостоятельной работы:
· Вариант 1:
· Определить, принадлежит ли точка с координатами (x,y) выделенной области (см. Рисунок4). Построить диаграмму, отображающую заданную область и точки.
· Таблица содержит следующие данные об учениках школы: фамилия, имя, возраст, и рост ученика. Сколько учеников могут заниматься в баскетбольной секции, если туда принимают детей с ростом не менее 160 см? Возраст не должен превышать 13 лет. Построить блок-схему, реализующую алгоритм решения задачи.
· 
· Рисунок 4
· Вариант 2:
· Определить, принадлежит ли точка с координатами (x,y) выделенной области (см. Рисунок5). Построить диаграмму, отображающую заданную область и точки.
· Есть данные об оценках, полученных при поступлении в вуз абитуриентами на математический факультет: по русскому языку, математике и информатике. Определить средний балл и количество поступивших абитуриентов по проходному баллу. Построить блок-схему, реализующую алгоритм решения задачи.
· 
· Рисунок 5
· Вариант 3:
· Определить, принадлежит ли точка с координатами (x,y) выделенной области (см. Рисунок6). Построить диаграмму, отображающую заданную область и точки.
· Есть информация о росте и весе женщин и мужчин. Определить, кому стоит худеть, а кому нет. Если вес больше чем (рост-100) в 1,5 раза, то срочно нужно худеть. Построить блок-схему, реализующую алгоритм решения задачи.
· 
· Рисунок 6
· Вариант 4:
· Определить, принадлежит ли точка с координатами (x,y) выделенной области (см. Рисунок7). Построить диаграмму, отображающую заданную область и точки.
· При температуре воздуха зимой до –20° С потребление угля тепловой станции составляет 10 тонн в день. При температуре от –30°С до -20°С дневное потребление увеличивается на 5 тонн, если температура воздуха ниже -30°С, то потребление увеличивается еще на 7 тонн. Составить таблицу потребления угля тепловой станции за неделю. Сколько дней температура воздуха была ниже -30°С? Построить блок-схему, реализующую алгоритм решения задачи.
· 
· Рисунок 7