Классифицировать дефекты на макроуровне (в заготовках и изделиях) принято на технологические, конструкционные и эксплуатационные.
3.1. Технологические дефекты в полуфабрикатах и изделиях типа пор, расслоений, трещин, складок, подмятий, инородных включений, искривлений слоев или волокон в плоскости слоя, зон с повышенным или пониженным (непроклей) содержанием связующего возникают в композитах в процессе изготовления, и для их исключения необходима тщательная отработка и стабильность технологических режимов. Поэтому технологии должны быть «безлюдными», что исключает «человеческий фактор» (типа попадания грязи, нарушение составов, температур, скоростей и усилий прикатки слоев препрега), а также защищает человека от воздействия вредных выделений при полимеризации смол (матриц) в процессе отверждения изделий. Например, при автоматизированной выкладке из препрегов крупногабаритных изделий сложной кривизны (типа крыла самолета) требуется подбирать конструкцию, размеры и усилия прикатного ролика, чтобы обеспечить ровное (без образования волн) выкладывание препрега на форму. Несущая подложка, на которой препрег транспортируется в рабочую зону, должна иметь определенную прочность и степень склейки с препрегом, чтобы исключить ее попадание в материал и обеспечить ее своевременное отделение непосредственно перед выкладкой препрега на изделие.
Изгибы волокон при их однонаправленной укладке приводят к снижению модуля упругости, которое оценивается по формуле типа /11/ Ед/Ео = (1 + f2)-1, где Ед, Ео модули упругости дефектного и бездефектного композита, соответственно, f – относительная амплитуда изгиба волокон или слоев.
Отклонение волокон от заданного направления существенно изменяет свойства композита, поэтому технологии изготовления деталей и вырезки образцов для испытаний требуют новых методов тщательного контроля углов, что не столь важно при изготовлении образцов из изотропных металлов. Наиболее заметно влияние разориентации при продольном нагружении вдоль волокон однонаправленных композитов. Для стекло- или углепластиков прочность практически не снижается и равна s(0) в диапазоне углов между направлениями нагрузки и волокон от 0 до a* = 5-70, когда разрушение происходит в результате разрыва волокон. Такая малая разориентация имеет даже определенные преимущества при усталостном нагружении, так как затруднено продольное расщепление композита. Слабая искривленность волокон – аналог природной свилеватости древесины, препятствующей ее раскалыванию. Однако, при больших углах разориентации a>a* происходит резкое снижение прочности s(a), которую можно оценить приближенной формулой s(a) = s(90)/(sin2a + m sina сosa), где s(0), s(90) - прочности под углами 00 и 900 к направлению волокон, m – экспериментальная константа, равная отношению поперечной прочности s(90) к прочности при сдвиге. По этой формуле a* =arctg½ [(z-1) m + Ö((1-z)2m2 + 4z)] @ arctg s(90)/ms(0) »60, поскольку z=s(90)/s(0)<<1 (» 0.05). Меньшая разориентация волокон практически неопасна, большая, чем a* – недопустима.
3.2. Конструкционные дефекты. К ним относятся отверстия, утолщения, соединения “композит-металл”, представляющие наибольшую проблему в конструировании композитных изделий. Традиционные для металлов методы соединения: сварка, резьбовое соединение для полимерных композитов напрямую неприменимы, а болтовые и заклепочные соединения малоэффективны, так как при сверлении отверстий перерезаются несущие волокна. Наиболее перспективно изготавливать отверстия заранее в незатвердевшей заготовке путем выкладывания препрегов на форму с цилиндрическими заостренными выступами по месту будущих отверстий. При этом волокна не разрываются, а раздвигаются, “обтекая” отверстие со всех сторон, и несущая способность такого соединения возрастает примерно на 40%. Широко используются также клеемеханические соединения, зиговые (ступенчатые) замки, прошивка тонкими стальными “гвоздями”, проволокой. С уменьшением примерно до 1 мм диаметра заклепки-“гвоздя”, который вводится в ещё не застывшее изделие, несущая способность соединения возрастает на 20-50%. Вообще, любое соединение требует изменения формы сечения и вызывает концентрацию напряжений, что приводит к снижению несущей способности. Разрабатываются методы расчета и оптимизации равнопрочных соединений, в которых различные виды разрушения возникают одновременно при наибольшей нагрузке, что обеспечивает равномерный коэффициент запаса по различным элементам и снижает вес изделия. Например, в заклепочном соединении возможны срез заклепки, смятие материала под заклепкой, поперечный разрыв детали по линии, соединяющей ряд заклепок, вырывание заклепки из детали. Анализ различных механизмов разрушения позволяет выбрать оптимальные размеры соединения, диаметр заклепок, расстояние между ними, чтобы эти виды разрушения возникали одновременно. Следует отметить необходимость «композитных» решений при создании соединений. «Металлические» методы неэффективны из-за низкой сдвиговой прочности композитов, и поэтому надо разрабатывать специальные типы крепления, такие как, например, придуманы человечеством для деревянных силовых деталей (ручки топора или молотка, шиповые соединения в строительстве, крепление хомута к оглобле в конской упряжи) без сверления традиционных отверстий. Вообще, композитные технологии позволяют обойти эту проблему путем интегрального изготовления изделия с минимальным числом соединений.
3.3 Эксплуатационные дефекты. К ним можно отнести: разрывы волокон, растрескивание матрицы, расщепления и расслоения с возможным выпучиванием поверхностных слоев при сжатии. Дефекты развиваются в условиях длительного статического нагружения, при много- и малоцикловой усталости, при динамическом нагружении, при пробивании и эрозии от абразивных частиц.
Одним из способов количественного описания процесса накопления повреждений и предсказания долговечности материала является введение параметра поврежденности w (доли разорванных волокон) и кинетического уравнения его роста ¶w/¶t =С(s/(1- w))n, где t – время, С, n – константы материала, s - приложенное (постоянное) напряжение в расчете на начальное неповрежденное сечение, s1 = s/(1- w), - истинное напряжение с учетом разрывов волокон. Критерий разрушения принимается либо в терминах критических истинных напряжений s1=s*, где s* – кратковременная прочность материала, и тогда долговечность
t*=(1+n)-1 С-1s- -n[1-(s/s*) n+1], либо в виде достижения параметром поврежденности критического значения w=w*(=1), и тогда t*=(1+n)-1 С-1s- -n. Таким образом, по результатам испытаний на длительную прочность при постоянном напряжении можно оценивать долговечность при других историях нагружения, используя, например, гипотезу о линейном суммировании повреждений.
При растяжении ортогонально армированного композита с полимерной матрицей первые микроразрушения проявляются в виде растрескивания матрицы в слоях с ортогональным расположением волокон, по отношению к направлению растяжения. Это приводит к снижению эффективной жесткости композита и на диаграмме деформирования появляется заметное изменение угла наклона. Вообще, первые разрушения возникают в слоях, имеющих меньшие предельные деформации.
В случае длительного (или циклического) растяжения вдоль волокон полимерная матрица проявляет чувствительность ко времени нагружения, и снижение прочности композита происходит из-за растрескивания матрицы, что приводит к росту эффективной длины (длины эквивалентного пучка волокон). Прочность самих волокон практически не зависит от времени нагружения, но кривые длительной прочности однонаправленных композитов с одинаковыми волокнами и различными матрицами могут сильно различаться из-за параметров длительной прочности матриц, характеризующих их повреждаемость - склонность к накоплению повреждений. Например, однонаправленные стеклопластики с эпоксидной и с полиэфирной матрицей при равной объемной доле волокон могут иметь почти одинаковую статическую прочность, но совершенно различную долговечность при длительном или циклическом нагружении. То же относится и к углепластикам, в матрицу которых для упрочнения введены нитевидные кристаллы, усы (вискеризация матрицы). При практически одинаковой статической прочности композитов с вискеризованной и с невискеризованной матрицами долговечность при нагрузках, составляющих 0.7 – 0.9 от статической прочности, для композита с вискеризованной матрицей в десятки и даже иногда в сотни раз выше. Для оценки долговечности однонаправленных композитов, растягиваемых вдоль волокон, удобно использовать соотношение t* = К(s0-s)(s0-s¥)n-1(s-s¥)-n, где коэффициенты К, n - отражают склонность матрицы к растрескиванию под действием постоянных или циклических напряжений и чувствительность волокон к состоянию матрицы (часто можно принять n = 2), s - приложенное постоянное напряжение, s0 – статическая прочность, s¥ - предел длительной прочности, то есть напряжение, при котором не происходит разрушения материала за время, выбранное базой испытания, или за бесконечное время.
4. ОЦЕНКА ОПАСНОСТИ ДЕФЕКТОВ .
4.1. Расчетные формулыдля оценки опасности дефектов. Наличие конструктивных отверстий в любых деталях вызывает местное повышение напряжений, которое численно характеризуется теоретическим коэффициентом концентрации напряжений Кт. Если бы разрушение начиналось при достижении наибольшим напряжением предела прочности sг для гладкого образца, то наличие концентратора напряжений снижало бы прочность элемента в Кт раз, то есть коэффициент снижения прочности равнялся бы 1/Кт. Расчеты упругих напряжений (аналитические, численные, экспериментальные) не вызывают принципиальных сложностей, и для заданных свойств материалв наибольшие значения напряжений не зависят от абсолютных размеров отверстия, а только от его формы. Так, для широкой всесторонне растягиваемой пластинки с круговым отверстием любого размера теоретический коэффициент концентрации напряжений равен 2. Если убрать часть напряжений и оставить только одноосное напряжение, то коэффициент концентрации не снизится, а напротив, возрастет и станет равным 3. Но реально прочность снижается не в 3 раза, а гораздо меньше, и она определяется эффективным коэффициентом концентрации напряжений Кэ = sг/sт (коэффициент снижения прочности 1/Кэ). Отметим три важные особенности, вызывающие сложности при расчете прочности в условиях неоднородного напряженного состояния, т.е. при наличии градиентов напряжений. 1. Кэ всегда меньше Кт. 2. Кэ растет с ростом абсолютного размера отверстия, а Кт не зависит от абсолютного размера отверстия (например, от радиуса кругового отверстия). 3. С увеличением «остроты» отверстия (в/а ®0 для эллиптического отверстия), при стремлении к 0 радиуса кривизны в кончике Кэ растет ограниченно, а Кт стремится к бесконечности, то есть разрушение должно было бы начаться при любом приложенном напряжении. Эти противоречия делают неприемлемым применение обычного критерия разрушения в терминах наибольших напряжений, если имеются существенные градиенты, и расчеты распределения напряжений становятся явно недостаточными, способными привести к значительным погрешностям (рис. 4). Рассмотрим особенности расчетов на прочность на примере ортотропной пластины с эллиптическим отверстием при одноосном равномерном растяжении вдоль малой полуоси эллипса в. Теоретический коэффициент концентрации напряжений: Кт = 1 + а/в (b1+b2)/b1b2, где упругие константы материала b1b2 = (Ех/ Еу)1/2, (b1+b2) = (Еx/Gxy - 2nyx + 2(Еx/Еy)1/2 )1/2, Ех, Еу - модули Юнга в двух перпендикулярных направлениях упругой симметрии, nyx - коэффициент Пуассона, Gxy - модуль сдвига в плоскости х-у. В изотропном случае b1=b2 =1 и (при а=в) Кт = 3, с ростом анизотропии Еx/Еy ®0 Кт растет и, например, для кругового отверстия в углепластике Кт =5. Реальное снижение прочности из-за кругового отверстия не превышает 1.4-1.6. Один из подходов, объясняющих приведенные выше противоречия между Кт и Кэ в связи с размерами отверстий, основан на так называемой градиентной гипотезе, согласно которой разрушение начинается, когда наибольшее напряжение достигнет предела прочности, умноженного на некоторую убывающую функцию от градиента напряжений ¶s/¶x. В качестве простейшей гипотезы можно принять: Кэ = Кт /(1+(А ¶s/¶x)1/3) и объяснить приведенные выше противоречия. С ростом размера отверстия градиент ¶s/¶x снижается и Кэ становится ближе к Кт. С повышением остроты отверстия различие между Кт и Кэ, напротив, растет, и даже для острых трещин, когда Кт обращается в бесконечность, Кэ остается конечным. Здесь коэффициент А имеет размерность длины, отнесенной к напряжению, и эта длина имеет смысл «характерного размера материала», некоего фундаментального понятия в механике разрушения, которое может быть введено различными способами, на основе разных моделей. Например, на основе гипотезы «слабого звена», когда материал представляется последовательно соединенными элементами, некой «цепью», разрушение которой связано с нарушением условия прочности слабейшего элемента. Для статистического анализа такой задачи необходимы сведения о распределении значений локальной прочности по объему материала (по длине волокна), а при этом неявно вводится характерный размер элемента, содержащего дефект. В такой постановке задачи необходимо искусственное разбиение материала на элементарные объемы, каждый из которых наделяется случайной прочностью. Характерный размер такого элементарного объема, по сути, является «подгоночным», феноменологическим параметром, подбираемым из условия соответствия с опытными данными.
Другая гипотеза состоит в том, что разрушение начинается тогда, когда напряжения, усредненные по некоторому характерному объему около вершины трещины или вычисленные на некотором характерном расстоянии от вершины трещины, достигают критического значения, равного пределу прочности. Длина зоны усреднения или расстояние до вершины трещины являются характерным размером материала, определяемым в опыте, и он равен обычно нескольким миллиметрам, то есть не связан прямо с диаметром волокон. Важно отметить, что он, в идеале, не должен зависеть от размеров и формы отверстия, хотя эта гипотеза не вполне согласуется с опытами. Такой подход также объясняет масштабный эффект в условиях концентрации напряжений и позволяет с единых позиций рассматривать влияние гладких отверстий и острых трещин на прочность материалов.
Применительно к композитам с полимерной матрицей хорошие результаты дает и другая простая модель двухстадийного разрушения /6/. Она основана на том, что на контуре отверстия первоначально выполняются условия разрушения матрицы в стороне от дна отверстия (т. В на рис. 2), а не условия разрыва волокон в точке А. Таким образом, на первой стадии происходит частичный выход из строя материала вокруг трещины или отверстия, то есть происходит как бы «затупление» отверстий до некоторого значения радиуса кривизны у дна, являющегося константой материала, его характерным размером. На основе такой модели ясно видно, как снимаются все три вышеуказанных противоречия. 1. Кэ меньше Кт, так как условный радиус кривизны затупленного отверстия больше реального, 2. Кэ растет с ростом реального размера отверстия, так как реальный радиус приближается к условному (если реальный радиус превышает условный, составляющий обычно несколько сотен миллиметров, то приходится считать, что Кэ = Кт, но это редкая ситуация: отверстия под заклепки, например, имеют диаметр всего 4-6 мм), 3. Для острых трещин (надрезов) эффективный коэффициент концентрации Кэ конечен и практически равен Кэ для отверстия с диаметром, равным длине трещины, что подтверждается в эксперименте. Аналогичная двухстадийная (очевидная из рис. 2, b, с) модель разрушения однонаправленного композита около отверстий /8/ позволяет оценить эффективный коэффициент концентрации напряжений около оставшейся после расщепления выточки с прежним радиусом кривизны у дна, но с уменьшенной глубиной, которую можно рассчитать, зная, где на контуре достигают наибольшего значения касательные напряжения, вызывающие расщепление вдоль поверхности раздела. Для оставшейся «мелкой» выточки коэффициент концентрации напряжений равен в случае кругового отверстия Кэ = 1.4 -1.6, что согласуется с экспериментами, а с ростом отношения а/b, с ростом остроты первоначального отверстия, глубина оставшейся выточки убывает вместе с радиусом кривизны в кончике отверстия, поэтому расчетное значение коэффициента концентрации напряжений хотя и растет, но ограниченно. Предельный коэффициент концентрации напряжений около отверстия произвольной остроты в расщепляющемся композите не может превышать значения 1.82, которое можно использовать в качестве верхней оценки при расчетах на прочность композитных изделий с отверстиями или трещинами в случае растяжения вдоль волокон.
4. 2.Расслоения при сжатии, кручении, изгибе. Одним из характерных видов разрушения слоистых композитов при сжатии является возникновение межслойных продольных трещин, множественное расслоение или расщепление композитов и выпучивание образовавшихся полосок. Критическое напряжение при этом на основе энергетического критерия типа Гриффитса может быть оценено следующим выражением /7/ s = 5/2(к Е3 g2 L-2)1/5, где g - удельная работа расслоения, Е – модуль Юнга вдоль направления сжатия, L - длина сжимаемого прямоугольного элемента, к – зависит от условия закрепления концов (к= p2/12 для незащемленных концов стержня), но в силу степени 1/5 эта зависимость довольно слабая. Аналогично, при поперечном трехточечном изгибе силой Р композитной балки с прямоугольным сечением шириной b и высотой h, с пролетом L критическая нагрузка может быть оценена из энергетического условия, в предположении, что накопленная упругая энергия при изгибе достигает значения, равного необходимой работе расслоения по площади bh и упругой энергии расслоенной на 2 части балки (толщина каждой половины равна h/2) при прежнем значении прогиба. Считается, что расслоение балки происходит так быстро, что прогиб не успевает измениться, и внешняя сила Р не производит в процессе расслоения дополнительной работы. В этом случае критическая сила равна Р=(4bh/L)(2Egh/3)1/2. Критическое касательное напряжение t=(h/L)(6Eg /h)1/2 оказывается зависящим не только от геометрии балки (от отношения h/ L), но и от абсолютных размеров h или L. Это есть подтверждаемое в опытах проявление масштабного эффекта, когда прочность большой детали оказывается меньше прочности, определенной на стандартных образцах небольших размеров (6х6х40 мм).
Критический момент при расслоении композитного стержня, испытывающего кручение, также может быть оценен из сравнения накопленной упругой энергии в закрученном стержне и в двух половинках стержня при том же угле закручивания. Разности этих энергий должно быть достаточно для осуществления работы расслоения. Оценка критического крутящего момента показывает, что рассчитанное стандартным образом наибольшее касательное напряжение при кручении не является постоянным в момент разрушения стержней различных размеров, что говорит о необходимой осторожности, с которой следует применять традиционные расчеты критических напряжений для композитов, разрушающихся расслоением. Такой подход позволяет оценить влияние на прочность трещин расслоения и указать критические напряжения, крутящий момент или угол закручивания, когда межслойный дефект начнет развиваться, приводя к потере несущей способности детали.
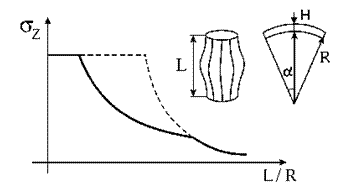Интересен механизм разрушения при сжатии однонаправленных труб или стержней кругового сечения в виде множественного продольного расщепления с одновременным выпучиванием образовавшихся полосок, число которых можно рассчитать. Разрушенная при сжатии труба приобретает форму китайского фонарика (рис. 5.), по аналогии с разрушением стержня бамбука при сжатии, и критическое напряжение для тонкостенной трубы выражается в виде: s = 1.2(Е5 g4 R-2 L-2)1/9, где R, L- радиус и длина трубы.
Изложенные выше подходы легко распространить на случай, когда в стержне, балке, трубе уже есть трещина расслоения площадью S. Энергетический баланс остается в силе с точностью до замены всей площади сечения на оставшуюся площадь при вычитании S. Таким 
образом, расчет прочности композитных элементов при наличии дефектов типа расслоений требует специальных подходов и не может осуществляться только на основе традиционных расчетов распределения напряжений в элементах конструкций.
4.3. Места соединений «композит-металл». В любых изделиях (и в металлических, и в композитных) места соединений относятся к наиболее слабым, дефектным, так как в этих местах неизбежно возникают изменения формы сечения (отверстия, резьба) или состава материала (сварка, склейка), что связано с концентрацией напряжений. С появлением композитных материалов изменяется подход к конструированию, так как создание конструкции происходит одновременно с созданием материала. Точно также происходит и в живой природе, когда сообразно воздействию внешних нагрузок изменяется структура материала, и наиболее прочные связи располагаются по линиям действия основных нагрузок. Например, корни деревьев (классических биокомпозитов), работающие преимущественно на растяжение, имеют структуру, отличную от структуры ствола, который подвергается в основном изгибу и сжатию, а в местах соединения корней ствола происходит врастание одной структуры в другую. Это биологическое крепление настолько прочно, что никогда не разрушается под действием естественных нагрузок (либо дерево вырывается из земли с корнями, либо ломается в стволе). К таким оптимальным соединениям (к которым можно отнести также крепление сучьев к стволу и корней к почве) еще соединениям только предстоит подойти в композитном конструировании. Большая часть применяемых соединений композитов есть по сути - варианты традиционных методов крепления металлов: в композит вводится закладная металлическая деталь, которую затем крепят на заклепках, сваркой, на резьбе и т.п. К наиболее перспективным следует отнести клеемеханические соединения с использованием заклепок малого диаметра и с нанесением отверстий не путем сверления, а в неотвержденном состоянии путем раздвигания волокон при выкладке заготовки на готовые штыри по месту будущих отверстий. Будущее, видимо, за технологиями типа плетения, позволяющими создавать оптимальные места крепления, управляя направлениями и натяжением волокон.
Заключение. Прочность материалов определяется дефектами на различных структурных уровнях. Необходимы специальные расчетные модели для оценки опасности различных дефектов. Рациональное проектирование композитов позволяет снижать влияние дефектов на прочность за счет реализации механизмов остановки и затупления трещин и путем создания специальных способов соединения деталей.
СПИСОК ЛИТЕРАТУРЫ
1. Griffith A.A. – Philos. Trans. Roy. Soc. London, 1920, v. A 221, p. 163.
2. Гордон Дж. Почему мы не проваливаемся сквозь пол (перев. с анг. С.Т.Милейко, под ред. Ю.Н. Работнова) М., “Мир”, 1971, 272 с.
(Gordon J. The new science of strong materials or why you don’t fall through the floor. Penguin Books Harmondsworth. 1968.)
3. Cook J., Gordon J.E. A mechanism for the control of crack propagation in all-brittle systems. Proc. Roy. Soc. Ser. A., 1964, v. 282, No. 1391, p. 132-144.
4. Полилов А.Н. Объяснение масштабного эффекта на основе энергетического критерия разрушения. Изв. АН СССР. Механика твердого тела. 1984, № 1, с 106-110.
5. Полилов А.Н. Торможение трещины поверхностью раздела. Изв. АН СССР. МТТ. 1974. №1, с. 68-71.
6. Полилов А.Н. Схема предразрушения композитов около отверстий. Изв. АН СССР. МТТ. 1982. №3, с. 110-117.
7. Полилов А.Н., Работнов Ю.Н. Развитие расслоений при сжатии композитов. Изв. АН СССР. МТТ. 1983. №4, с. 166-171.
8. Полилов А.Н., Работнов Ю.Н. Разрушение около боковых выточек композитов с низкой сдвиговой прочностью. Изв. АН СССР. МТТ. 1976, №6, с. 112-119.
9. Работнов Ю.Н., Полилов А.Н. О разрушении композитных труб по форме китайского фонарика. Механика композитных материалов. 1983, № 3, с.. 548-550.
10. Лехницкий С.Г. Теория упругости анизотропного тела. М.-Л., Гостехиздат. 1950, 300с.
(Lekhnitskii S.G. Theory of Elasticity of an Anisotropic Body. (J.J.Brandstatter, ed; P. Fern, translator). 1963. Holden-Day, San-Francisco, California, USA.
11. Композиционные материалы (справочник под ред. В.В. Васильева, Ю.М. Тарнопольского). М., “Машиностроение”, 1990. 510 с.
12. Mechanics of Composites (I.F. Obraztsov and V.V. Vasil’ev, ed., V.I. Ilyushenko, translator). MIR Publishers, Moscow. 1982. 280 p.