Переменными (неизвестными) транспортной задачи являются xij, i=1,2,...,m j=1,2,...,n — объемы перевозок от i-го поставщика каждому j-му потребителю.
Эти переменные могут быть записаны в виде матрицы перевозок:

Так как произведение Cij*Xij определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны:

По условию задачи требуется обеспечить минимум суммарных затрат.
Следовательно, целевая функция задачи имеет вид:
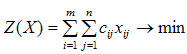
Система ограничений задачи состоит из двух групп уравнений.
Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью и имеет вид:

Вторая группа из n уравнений выражает требование удовлетворить запросы всех n потребителей полностью и имеет вид:
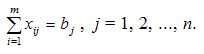
Учитывая условие не отрицательности объемов перевозок математическая модель выглядит следующим образом:

В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.:

Такая задача называется задачей с правильным балансом, а модель задачи закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а модель задачи — открытой.
10. Основные понятия теории игр. Примеры простейших матричных игр.
Игра – упрощенная формализованная модель конфликтной ситуации.
Игрок – одна из сторон в игровой ситуации. В зависимости от постановки задачи, стороной может выступать коллектив или даже целое государство.
Каждый игрок может иметь свои стратегии. Стратегией i-го игрока x2 называется одно из возможных решений из множества допустимых решений этого игрока.
По количеству стратегий игры делятся на конечные, в которых число стратегий ограничено, и бесконечные, которые имеют бесконечно много различных стратегий.
Каждый из n участников игры может выбирать свою стратегию. Совокупность стратегий x=x1,x2,…,xn, которые выбрали участники игры, называется игровой ситуацией.
Оценить ситуацию x с точки зрения преследуемых ЛПР целей можно, построив целевые функции (или критерии качества), ставящие в соответствие каждой ситуации x числовые оценки f1(x),f2(x),…,fn(x) (например, доходы фирм в ситуации x или их затраты и т. д.).
Тогда цель i– го ЛПР формализуется следующим образом: выбрать такое свое решение xi, чтобы в ситуации x=x1,x2,…,xn число fi(x) было как можно большим (или меньшим). Однако достижение этой цели от него зависит лишь частично, поскольку другие участники игры влияют на общую ситуацию x с целью достижения своих собственных целей (оптимизируют свои целевые функции). Значение целевой функции в той или иной игровой ситуации можно назват ь выигрышем игрока в этой ситуации.
По характеру выигрышей игры можно разделить на игры с нулевой и ненулевой суммой. В играх с нулевой суммой сумма выигрышей в каждой игровой ситуации равна нулю. Игры двух игроков с нулевой суммой называются антагонистическими. В этих играх выигрыш одного игрока равен проигрышу другого.
В играх с ненулевой суммой в выигрыше или проигрыше могут оказаться все участники игры.
По виду функции выигрышей игры можно разделить на матричные, биматричные, непрерывные, сепарабельные и т. д.
Матричными играми называются конечные игры двух игроков с нулевой суммой. В этом случае номер строки матрицы соответствует номеру стратегии Ai игрока 1, а номер столбца – номеру стратегии Bj игрока 2.
Элементами матрицы aij является выигрыш игрока 1 для ситуации (реализации стратегий) AiBj. В силу того, что рассматривается матричная игра с нулевой суммой, выигрыш игрока 1 равен проигрышу игрока 2.
Можно показать, что всякая матричная игра с известной матрицей платежей сводится к решению задачи линейного программирования.
Поскольку в прикладных задачах экономики и управления ситуации, сводящиеся к матричным играм, встречаются не очень часто, мы не будем останавливаться на решении этих задач.
Биматричная игра – это конечная игра двух игроков с ненулевой суммой. В этом случае для каждой игровой ситуации AiBj каждый из игроков имеет свой выигрыш aij для первого игрока и bij– для второго игрока. К биматричной игре сводится, например, поведение производителей на рынках несовершенной конкуренции.
По степени неполноты информации, которой обладают ЛПР, игры делятся на стратегические и статистические.
Стратегические игры – это игры в условиях полной неопределенности.
Статистические игры – это игры с частичной неопределенностью. В статистической игре всегда имеется один активный игрок, имеющий свои стратегии и цели. Другим игроком (пассивным, не преследующим своих целей) является природа. Этот игрок реализует свои стратегии (состояния природы) случайным образом, причем вероятность реализации того или иного состояния можно оценить с помощью статистического эксперимента.
Поскольку с теорией статистических игр тесно связана теория принятия экономических решений, то в дальнейшем мы ограничимся рассмотрением только этого класса игр.
11. Платежная матрица. Нижняя и верхняя цена игры.
Платежная матрица — это один из методов статистической теории решений, метод, который может оказать помощь руководителю в выборе одного из нескольких вариантов.
Шаг:1
Определим нижнюю цену игры - α
Нижняя цена игры α — это максимальный выигрыш, который мы можем гарантировать себе, в игре против разумного противника, если на протяжении всей игры будем использовать одну и только одну стратегию (такая стратегия называется "чистой").
Найдем в каждой строке платежной матрицы минимальный элемент и запишем его в дополнительный столбец (Выделен желтым цветом см. Табл.1).
Затем найдем максимальный элемент дополнительного столбца (отмечен звездочкой), это и будет нижняя цена игры.
Таблица 1
| Стратегии "B" | |||||
| Стратегии "A" | B1 | B2 | B3 | B4 | Минимумы строк |
| A1 | 1.45 | 2.12 | 0.75 | 4.01 | 0.75 |
| A2 | 3.52 | 1.87 | 0.18 | 12.7 | 0.18 |
| A3 | 6.08 | 4.43 | 11.0 | 6.01 | 4.43* |
В нашем случае нижняя цена игры равна: α = 4.43, и для того чтобы гарантировать себе выигрыш не хуже чем 4.43 мы должны придерживаться стратегии A3
Шаг:2
Определим верхнюю цену игры - β
Верхняя цена игры β — это минимальный проигрыш, который может гарантировать себе игрок "В", в игре против разумного противника, если на протяжении всей игры он будет использовать одну и только одну стратегию.
Найдем в каждом столбце платежной матрицы максимальный элемент и запишем его в дополнительную строку снизу (Выделена желтым цветом см. Табл.2).
Затем найдем минимальный элемент дополнительной строки (отмечен плюсом), это и будет верхняя цена игры.
Таблица 2
| Стратегии "B" | |||||
| Стратегии "A" | B1 | B2 | B3 | B4 | Минимумы строк |
| A1 | 1.45 | 2.12 | 0.75 | 4.01 | 0.75 |
| A2 | 3.52 | 1.87 | 0.18 | 12.7 | 0.18 |
| A3 | 6.08 | 4.43 | 11.0 | 6.01 | 4.43* |
| Максимумы столбцов | 6.08 | 4.43+ | 11.0 | 12.7 |
В нашем случае верхняя цена игры равна: β = 4.43, и для того чтобы гарантировать себе проигрыш не хуже чем 4.43 противник (игрок "B") должен придерживаться стратегии B2
Шаг:3
Сравним нижнюю и верхнюю цены игры, в данной задаче они совпадают, т.е. α = β = 4.43. Это значит, что игра имеет решение в так называемых "чистых", минимаксных стратегиях. Это как раз те стратегии для игроков "A" и "B" которые были найдены выше, при поиске нижней и верхней цен игры. То есть, в нашем случае для игрока "A" оптимальной будет стратегия A3, а для игрока "В" - B2. Нетрудно заметить, что элемент платежной матрицы расположенный на пересечении чистых оптимальных стратегий (строка 3, столбец 2) является одновременно минимальным в строке и максимальным в столбце (отмечен знаками *+ см. Табл.2). Такие элементы называются седловыми точками, именно их наличие и определяет существование решения игры в чистых стратегиях, а его значение (в нашем случае 4.43) совпадает с чистой ценой игры или просто ценой игры - v. Пара оптимальных стратегий, в играх имеющих седловую точку, всегда проходит через последнюю.
Таблица 2
| Стратегии "B" | |||||
| Стратегии "A" | B1 | B2 | B3 | B4 | Минимумы строк |
| A1 | 1.45 | 2.12 | 0.75 | 4.01 | 0.75 |
| A2 | 3.52 | 1.87 | 0.18 | 12.7 | 0.18 |
| A3 | 6.08 | 4.43*+ | 11.0 | 6.01 | 4.43* |
| Максимумы столбцов | 6.08 | 4.43+ | 11.0 | 12.7 |
Ответ:
Нижняя цена игры, верхняя цена игры и чистая цена игры: α = β = v = 4.43;
Пара оптимальных стратегий: A3B2
12. Основные приемы упрощение игр.
Если платежная матрица игры не содержит седловой точки, то задача определения оптимальной смешанной стратегии тем сложнее, чем больше размерность матрицы. Поэтому для игр с платежными матрицами большой размерности отыскание решения можно упростить, если уменьшить их размерность путем вычерчивания дублирующих изведомо невыгодных стратегий, а также замены некоторых групп чистых стратегий смешанными.
Опр.: Если в матрице  игры все элементы строки(столбца) равны соответствующим элементам другой строки(столбца), то соответствующие строкам(столбцам) стратегии называются дублирующими.
игры все элементы строки(столбца) равны соответствующим элементам другой строки(столбца), то соответствующие строкам(столбцам) стратегии называются дублирующими.
Опр.: Если в матрице  игры все элементы некоторой строки определяют стратегию
игры все элементы некоторой строки определяют стратегию  игрока I не больше соответсвующих элементов другой строки, то стратегия
игрока I не больше соответсвующих элементов другой строки, то стратегия  называется заведомо невыгодной.
называется заведомо невыгодной.
Опр.: Если в матрице  игры все элементы некоторого столбца, определяющие стратегию
игры все элементы некоторого столбца, определяющие стратегию  игрока II не меньше соответствующих элементов другого столбца, то стратегия
игрока II не меньше соответствующих элементов другого столбца, то стратегия  называется заведомо невыгодной.
называется заведомо невыгодной.
Пример:
стратегия  дублирует стратегию
дублирует стратегию  , поэтому любую из них можно вычеркнуть.
, поэтому любую из них можно вычеркнуть.
Если сравнить  и
и  , то можно заметить, что все элементы
, то можно заметить, что все элементы  не превышают соответствующих элементов
не превышают соответствующих элементов  . Значит стратегия
. Значит стратегия  для нас, желающих выиграть заведомо невыгодна. Вычеркивая
для нас, желающих выиграть заведомо невыгодна. Вычеркивая 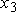 и
и  приведем матрицу к более простому виду.
приведем матрицу к более простому виду.
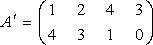
Для второго игрока стратегия 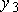 заведомо невыгодна. Вычеркивая ее получим
заведомо невыгодна. Вычеркивая ее получим

Таким образом игра  сведена к игре
сведена к игре  . Иногда удается упростить игру искусственным введением вместо чистых стратегий смешанных.
. Иногда удается упростить игру искусственным введением вместо чистых стратегий смешанных.
Пример:

Из матрицы видна “симметрия” элементов стратегий  и
и  ,
, 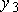 и
и  , а также
, а также  и
и  . Если эти стратегии входят в решение, то только с одинаковыми вероятностями
. Если эти стратегии входят в решение, то только с одинаковыми вероятностями  ,
,  и
и  . Возникает желание заранее объединить
. Возникает желание заранее объединить  и
и  в одну смешанную стратегию
в одну смешанную стратегию  состоящую наполовину из
состоящую наполовину из  и на половину из
и на половину из  . Аналогично можно попытаться поступить со стратегиями
. Аналогично можно попытаться поступить со стратегиями 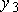 и
и  объединив их в
объединив их в  куда они войдут с одинаковыми вероятностями 0.5. Получим
куда они войдут с одинаковыми вероятностями 0.5. Получим

Стратегии  и
и  дублирующие и одну из них можно вычеркнуть
дублирующие и одну из них можно вычеркнуть

Таким образом из матрицы 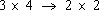 .
.
13. Основные принципы приведения матричной игры к задаче линейного программирования.
Игра m × n в общем случае не имеет наглядной геометрической интерпретации. Ее решение достаточно трудоемко при больших m и n, однако принципиальных трудностей не имеет, поскольку может быть сведено к решению задачи линейного программирования. Покажем это. Пусть игра m × n задана платежной матрицей p = (aij), i = 1, 2,..., m; j = 1, 2,..., n. Игрок А обладает стратегиями A1 , A2 ,..., Am , игрок В — стратегиями B1 , B2 ,..., Bm . Необходимо определить оптимальные стратегии S*A = (p*1 , p*2,..., p*m) и S*B = (q*1 , q*2,..., q*n), где p*i, q*j — вероятности применения соответствующих чистых стратегий Ai, Bj, p*1 + p*2 +...+ p*m =1, q*1 + q*2 +...+ q*n = 1.
Оптимальная стратегия S*A удовлетворяет следующему требованию. Она обеспечивает игроку А средний выигрыш, не меньший, чем цена игры v, при любой стратегии игрока В и выигрыш, равный цене игры v, при оптимальной стратегии игрока B. Без ограничения общности полагаем v > 0: этого можно добиться, сделав все элементы aij ≥ 0. Если игрок А применяет смешанную стратегию S*A = (p*1 , p*2,..., p*m) против любой чистой стратегии Bj игрока В, то он получает средний выигрыш, или математическое ожидание выигрыша aj = a1j p1 + a2j p2 +...+ am j pm, о = 1, 2,..., n (т.е. элементы j -го столбца платежной матрицы почленно умножаются на соответствующие вероятности стратегий A1 , A2 ,..., Am и результаты складываются).
Для оптимальной стратегии S*A все средние выигрыши не меньше цены игры v, поэтому получаем систему неравенств:

| (3.11) |
Каждое из неравенств можно разделить на число v > 0. Введем новые переменные:
| x1 = p1/v, x2 = p2/v,..., pm/v | (3.12) |
Тогда система (11) примет вид:

| (3.13) |
Цель игрока А — максимизировать свой гарантированный выигрыш, т.е. цену игры v.
Разделив на v ≠ 0 равенство p1 + p2 +...+ pm = 1, получаем, что переменные x1 (i = 1, 2,..., m) удовлетворяют условию: x1 + x2 +...+ xm = 1/v. Максимизация цены игры v эквивалентна минимизации величины 1/v, поэтому задача может быть сформулирована следующим образом: определить значения переменных xi ≥ 0, i = 1, 2,..., m, так, чтобы они удовлетворяли линейным ограничениям (13) и при этом линейная функция
| Z = x1 + x2 +...+ xm, | (3.14) |
обращалась в миниму м. Это задача линейного программирования. Решая задачу (3.13)—(3.14), получаем оптимальное решение p*1 + p*2 +...+ p*m и оптимальную стратегию SA.
Для определения оптимальной стратегии S*B = (q*1 + q*2 +...+ q*n) следует учесть, что игрок В стремится минимизировать гарантированный выигрыш, т.е. найти  . Переменные q1 , q2,..., qn удовлетворяют неравенствам:
. Переменные q1 , q2,..., qn удовлетворяют неравенствам:

| (3.15) |
которые следуют из того, что средний проигрыш игрока В не превосходит цены игры, какую бы чистую стратегию не применял, игрок А.
Если обозначить
| yj = qj/v, j = 1, 2,..., n, | (3.16) |
то получим систему неравенств:

| (3.17) |
Переменные yj (1, 2,..., n) удовлетворяют условию 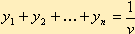 .
.
Игра свелась к следующей задаче
Определить значения переменных yj ≥ 0, j = 1, 2,..., n, которые удовлетворяют системе неравенств (3.17) и максимизируют линейную функцию
| Z' = y1 + y2 +...+ yn, | (3.18) |
Решение задачи линейного программирования (3.16), (3.17) определяет оптимальную стратегию S*B = (q*1 + q*2 +...+ q*n). При этом цена игры
| v = 1 / max, Z' = 1 / min Z | (3.19) |
Составив расширенные матрицы для задач (3.13), (3.14) и (3.17), (3.18), убеждаемся, что одна матрица получилась из другой транспонированием:

Таким образом, задачи линейного программирования (3.13), (3.14) и (3.17), (3.18) являются взаимно-двойственными. Очевидно, при определении оптимальных стратегий в конкретных задачах следует выбрать ту из взаимно-двойственных задач, решение которой менее трудоемко, а решение другой задачи найти с помощью теорем двойственности. Приведем примеры экономических задач, которые описываются игровыми моделями т х п и могут быть решены методами линейного программирования.
14. Общая постановка задачи динамического программирования.
Динамическое программирование (ДП) — метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми. Начало развития ДП относится к 50-м годам XX в. Оно связано с именем Р.Беллмана.
Если модели линейного программирования можно использовать в экономике для принятия крупномасштабных плановых решений в сложных ситуациях, то модели ДП применяются при решении задач значительно меньшего масштаба, например, при разработке правил управления запасами, устанавливающими момент пополнения запасов и размер пополняющего заказа; при разработке принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; при распределении дефицитных капитальных вложений между возможными новыми направлениями их использования; при составлении календарных планов текущего и капитального ремонта сложного оборудования и его замены; при разработке долгосрочных правил замены выбывающих из эксплуатации основных фондов и т. п.
В реально функционирующих больших экономических системах еженедельно требуется принимать микроэкономические решения. Модели ДП ценны тем, что позволяют на основе стандартного подхода с использованием при минимальном вмешательстве человека принимать такие решения. И если каждое взятое в отдельности такое решение малосущественно, то в совокупности эти решения могут оказать большое влияние на прибыль.
Приведем общую постановку задачи ДП. Рассматривается управляемый процесс, например, экономический процесс распределения средств между предприятиями, использования ресурсов в течение ряда лет, замены оборудования, пополнения запасов и т. п. В результате управления система (объект управления)  переводится из начального состояния
переводится из начального состояния  в состояние
в состояние 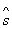 . Предположим, что управление можно разбить на
. Предположим, что управление можно разбить на 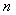 шагов, т.е. решение принимается последовательно на каждом шаге, а управление, переводящее систему
шагов, т.е. решение принимается последовательно на каждом шаге, а управление, переводящее систему  из начального состояния в конечное, представляет собой совокупность
из начального состояния в конечное, представляет собой совокупность 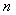 пошаговых управлений.
пошаговых управлений.
Обозначим через  управление на
управление на  -м шаге (
-м шаге (  ). Переменные
). Переменные  удовлетворяют некоторым ограничениям и в этом смысле называются допустимыми (
удовлетворяют некоторым ограничениям и в этом смысле называются допустимыми (  может быть числом, точкой в n-мерном пространстве, качественным признаком).
может быть числом, точкой в n-мерном пространстве, качественным признаком).
Пусть  — управление, переводящее систему
— управление, переводящее систему  из состояния
из состояния  в состояние
в состояние 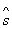 . Обозначим через
. Обозначим через  состояние системы после k-го шага управления. Получаем последовательность состояний
состояние системы после k-го шага управления. Получаем последовательность состояний  ,
,  , …,
, …,  ,
,  , …,
, …,  ,
,  , которую изобразим кружками (рис. 4.5).
, которую изобразим кружками (рис. 4.5).

15. Определение принципа оптимальности Беллмана.
Уравнение Беллмана (также известное как уравнение динамического программирования), названное в честь Ричарда Эрнста Беллмана, является достаточным условием для оптимальности, ассоциируемой с математическим методом оптимизации, называемым динамическим программированием и базируется на Принципе оптимальности Беллмана. Уравнение Беллмана представляет собой дифференциальное уравнение в частных производных с начальными условиями, заданными для последнего момента времени (т.е. справа), для функции Беллмана, которая выражает минимальное значение критерия оптимизации, которое может быть достигнуто, при условии эволюции системы из текущего состояния в некоторое конечное. А это в свою очередь позволяет перейти от решения исходной многошаговой задачи оптимизации к последовательному решению нескольких одношаговых задач оптимизации.
Понятие Уравнения Беллмана и функции Беллмана применяется только для непрерывных систем. Для дискретных систем аналогом выступает так называемое основное рекуррентное соотношение, являющееся формальной основой метода динамического программирования и выражающее достаточное условие оптимальности, и функция будущих потерь.
Формальные соотношения, выражающие достаточное условия оптимальности как для дискретных, так и для непрерывных систем могут быть записаны как для случая детерминированных, так и для случая стохастических динамических систем общего вида. Отличие заключается лишь в том, что для случая стохастических систем в правых частях этих выражения возникает условное математическое ожидание.
Принцип оптимальности Беллмана (также известный как принцип динамического программирования), названный в честь Ричарда Эрнста Беллмана, описывает действие математического метода оптимизации, называемого динамическим программированием. Он заключается в том, что на каждом шаге следует стремиться не к изолированной оптимизации функции {\displaystyle f_{k}\left(x_{k},\xi _{k}\right)}, а выбирать оптимальное управление {\displaystyle x_{k}^{*}} в предположении об оптимальности всех последующих шагов.
Принцип оптимальности: оптимальная стратегия имеет свойство, что какими бы ни были начальное состояние и начальное решение, последующие решения должны составлять оптимальный курс действий по отношению к состоянию, полученному в результате первого решения. Иными словами оптимальная стратегия зависит только от текущего состояния и цели, и не зависит от предыстории.
16. Математическая модель задачи распределения средств между предприятиями.
Для увеличения объёмов выпуска пользующейся повышенным спросом продукции, изготавливаемой 4 предприятиями города, выделены средства в размере 100 млн. руб. Использование i -ым предприятием x млн. руб. из указанных средств обеспечивает прирост выпуска продукции, определяемый значением fi(x).
Найти распределение средств между предприятиями, обеспечивающее максимальное увеличение выпуска продукции.

Целевая функция  при ограничениях:
при ограничениях:

Рассмотрим обратную схему Беллмана. Рекуррентные соотношения имеют вид:

Распределение ресурсов будем производить с точностью 20 единиц.
Согласно обратной схеме Беллмана показатель эффективности:
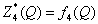 ;
;
 - показатель эффективности деятельности 1 предприятия.
- показатель эффективности деятельности 1 предприятия.
 - объединённый показатель эффективности деятельности 2 предприятий.
- объединённый показатель эффективности деятельности 2 предприятий.
Произведем вычисления значений функции 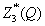 и представим их в таблице.
и представим их в таблице.

Произведем вычисления значений функции
 и представим их в таблице.
и представим их в таблице.

Объединённый показатель эффективности деятельности 4 предприятий - 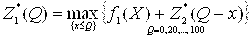 . Произведем вычисления значений функции
. Произведем вычисления значений функции  и представим их в таблице.
и представим их в таблице.


Из таблицы находим оптимальный план распределения выделенных средств. В результате вычислений получили, что максимальное значение функции цели составляет  .
.

Таким образом, в результате решения задачи распределения средств между предприятиями получили, что для обеспечения максимальной эффективности деятельности (прибыли) всех предприятий, равной 61 млн. руб., первому, второму и третьему предприятиям согласно оптимальному распределению не следует выделять деньги, четвертому предприятию необходимо выделить 100 млн. руб.