Рисунок 2.12 Схема распределения нагрузок на эксцентриковый вал
Найдем реакции опор в вертикальной плоскости
Рисунок 2.13 Схема реакций опор в вертикальной плоскости.
(2.49)
Определим изгибающий момент в вертикальной плоскости
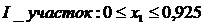
(2.50)
при x1 =0 M1Х =0
x1 =0,925 M1X =236111·0,925=218403 Н·м
(2.51)
при x2 =0 M2X =0
x2 =0,925 M2X =-218403 Н·м
Находим реакции опор в горизонтальной плоскости
Рисунок 2.14 Схема реакций опор в горизонтальной плоскости
(2.52)
(2.53)
Определим изгибающий момент в горизонтальной плоскости
(2.54)
при y 1 =0 M1Y =0
y1 =1,85 M1Y =8552,2 Н·м
(2.55)
при y 2 =0 M2Y =0
y2 =0,525 M2Y =-8552 Н·м
Опасным сечение эксцентрикового вала является точка приложения силы Qнаиб. Определим одинарный изгибающий момент в опасном сечении по формуле
(2.56)
Эквивалентный момент в этом сечении определим по формуле
(2.57)
Диаметр вала под шатуном определим по формуле
(2.58)
где [τ1] – допустимое тангенсальное напряжение [τ1] = 10 – 30 мПа
Принимаем d = 380 мм.
Определим диаметр выходного конца эксцентрикового вала по формуле
(2.59)
где М1 – крутящий момент на выходном конце вала
Учитывая ослабляющие сечения поточенной канавкой и ударные нагрузки, которые могут возрастать в 3 раза, принимаем dк = 300 мм.
Можно считать, что нормальные напряжения возникающие в поперечном сечении вала от изгиба, изгибаются по симметричному циклу
(2.60)
где W – момент сопротивления вала
(2.61)
После подстановки найденного значения в формулу (2.60) получим
Касательные напряжения от нулевого цикла для сечения под шатунов определим по формуле
(2.62)
(2.63)
После подстановки найденного значения в формулу (2.62) получим
Коэффициент запаса прочности по нормальным напряжениям определим по формуле
|
|
(2.64)
где ε-1 – предел выносливости при изгибе, Н/мм2;
κδ – эффективный коэффициент напряжений при изгибе, κδ =2,5;
εδ – максимальных фактор для нормальных напряжений, εδ = 0,42;
ψδ – коэффициент, учитывающий влияние постоянной составляющей цикла на усталостную прочность;
εm – среднее напряжения циклов нормальных напряжений, εm =0.
Предел выносливости при изгибе
(2.65)
где 
- предел прочности для стали 40хН, = 740 Н/мм2
После подстановки найденных значений параметров в формулу (2.69) получим
Коэффициент запаса прочности по касательным напряжениям определим по формуле
(2.66)
где τ -1 – предел выносливости при кручении, Н/мм2;
κτ – эффективный коэффициент концентрации напряжений при кручении, κδ =1,8;
ψτ –коэффициент, учитывающий влияние постоянной составляющей цикла на усталостную прочность, ψτ = 0,15;
τ m – амплитуда и средние напряжения циклов касательных напряжений.
Определим предел выносливости при кручении по формуле
(2.67)
Н/мм2
После подстановки найденных значений параметров в формулу (2.71) получим
Общий коэффициент запаса прочности определим по формуле
(2.68)
Таким образом прочность и жесткость эксцентрикового вала в месте посадки шатуна обеспечена.
Эксцентриковый вал работает в очень трудных условиях, поэтому рассчитаем коэффициент запаса прочности при двукратных нагрузках.
Коэффициент запаса прочности по сопротивлению пластическим деформациям определим по формуле
(2.69)
где ξr – предел тягучести, ξr = 550 Н/мм2;
и 
- максимальные напряжения при двукратных нагрузках.
|
|
Этот коэффициент запаса прочности также достаточен.
