Уравнение Менделеева-Клапейрона достаточно хорошо описывает газ при низких давлениях и высоких температурах, когда он находится в условиях, далеких от условий конденсации и для газов при нормальных условиях.
Для реального газа, особенно при повышенных давлениях и низких температурах, модель идеального газа может оказаться неадекватной. В этом случае необходимо учитывать потенциальную энергию взаимодействия молекул газа между собой и размеры молекул.
Уравнение, описывающее реальный газ, сформулировал в 1873 г. нидерландский физик Ян Дидерик Ван-дер-Ваальс (1837-1923).
Уравнение Ван-дер-Ваальса описывает не только газообразное состояние, но и переход к жидкому и твердому состоянию. Предложенная модель реального газа учитывает факт того, что молекулы газа притягиваются на больших, но отталкиваются на малых расстояниях, близких к размеру молекулы.
Силы притяжения внутри газа скомпенсированы для каждой молекулы, поскольку действуют в среднем одинаково во все стороны. На молекулы, расположенные в тонком слое вблизи границ объема, действует некомпенсированная сила притяжения со стороны других молекул газа, направленная внутрь объема, которая создает дополнительное (внутреннее) давление.
Если уменьшать объем под действием внешнего давления, внутреннее давление растет быстрее внешнего. При равенстве давлений газ превращается в жидкость.
Сила внутреннего давления, действующая на молекулу поверхностного слоя газа должна быть пропорциональна концентрации молекул п в прилегающем внутреннем слое, а суммарная сила внутреннего давления пропорциональна еще и концентрации молекул п в поверхностном слое.
Таким образом, суммарное внутреннее давление пропорционально квадрату концентрации молекул газа
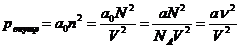(2)
где а 0и а – константы, связанные через число Авогадро, а= а 0 NA; п – концентрация молекул; N – количество молекул в V; объеме; ν – число молей.
Суммарное давление p ' внутри газа
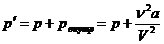(3)
где р – давление газа на стенку объема (по третьему закону Ньютона стенка действует на газ тем же давлением).
Поправка на действие сил отталкивания действует на меньших расстояниях и учитывает только парные взаимодействия между молекулами.
Суть ее сводится к учету размеров молекул. Ван-дер-Ваальс предложил в уравнение состояния включить не полный объем сосуда, а только свободный, доступный для движения молекул.
Каждая молекула уменьшает свободный для движения другой молекулы объем сосуда. При этом радиус исключаемой сферы вдвое превышает радиус молекулы rт (рисунок 2). Объем этой исключаемой сферы, очевидно, в 8 раз превышает объем Vm молекулы.
Это означает, что на каждую из двух рассматриваемых молекул (и на все остальные молекулы) приходится четырехкратный исключаемый объем молекулы 4Vm. Таким образом, на N находящихся в сосуде молекул необходимо исключить объем 4 N Vm.
Свободный объем будет равным
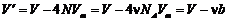(4)
где b= 4 NA Vm.
Подставив суммарное давление газа p ' и свободный объем V 'в уравнение состояния идеального газа, получим уравнение Ван-дер-Ваальса
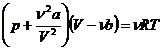(5)
где а и b – постоянные Ван-дер-Ваальса.
b – поправка на собственный объем молекул, учитывающая действие сил отталкивания между молекулами и равная учетверенному объему молекул, содержащихся в одном моле газа.
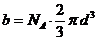(6)
Величина поправки а
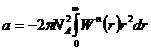,(7)
Теоретические оценки постоянных Ван-дер-Ваальса носят приближенный характер, более точно для каждого газа они определяются экспериментально.
Экспериментальные значения постоянных Ван-дер-Ваальса для некоторых газов приведены в таблице 4 Приложения.
Термодинамические процессы, приводящие к изменению агрегатного состояния вещества,называются фазовыми переходами.
Выделяют агрегатные состояния: твердое, жидкое, газообразное, др. Изменение агрегатного состояния обычно сопровождается скачкообразным изменением энтропии, плотности и других основных физических свойств вещества.
Уравнение Ван-дер-Ваальсаможно применять для качественных оценок изменений агрегатного состояния вещества.
Уравнение реального газа можно представить в виде зависимости давления газа от его объёма
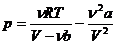(8)
Из уравнения видно, что при V→∞ доминирует левый член зависимости, и давление, как и для идеального газа, убывает по гиперболическому закону
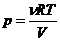(9)
При V→ 0 доминирует правый член зависимости (внутреннее давление), и давление растет пропорционально V -2
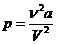(10)
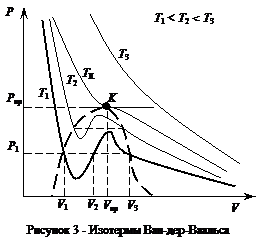При невысокой температуре имеют место два экстремума. При этом на изотермах имеется участок, где давление растет с увеличением объема, что не имеет физического смысла.
Экспериментальные изотермы состояния газа отличаются тем, что участок теоретической зависимости, где давление растет сувеличением объема, представляет собой горизонтальный участок, соответствующий сжижению газа, которое при заданной температуре происходит при постоянном давлении.
При повышении температуры этот участок уменьшается и превращается в точку. Эта точка называется критической. Значения давления, объема и температуры в этой точке называют критическими параметрами.
В критической точке кривая имеет точку перегиба, так что обращаются в ноль как первая, так и вторая производные. Из этих условий определяются критические параметры
, 
, 
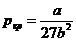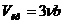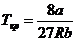.(11)
Критические параметры для некоторых газов приведены в таблице 4 Приложения.
При температуре выше критической вещество может существовать только в газообразном состоянии. При температуре ниже критической вещество может быть превращено в жидкость.
У гелия, водорода, кислорода и азота критические температуры низкие, и при нормальных условиях они являются газами.
У воды и ртути критические температуры высокие, поэтому при нормальных условиях эти вещества существуют в жидком и в газообразном состоянии.