Внутренняяэнергия реального газа, в отличие от идеального, дополнительно включает потенциальную энергию межмолекулярного взаимодействия. При этом соотношение между потенциальной энергией взаимодействия двух соседних молекул U M и кинетической энергией теплового движения молекулы, равной по порядку величины kТ, определяет состояние вещества.
Если U M«kT,то взаимодействием можно пренебречь – вещество находится в газообразном состоянии. Если U M ›› kT, то вещество твердое. Если U M ≈ kT, то вещество – в жидком состоянии.
Силы взаимодействия реального газа имеют электрическое или электромагнитное происхождения. Они определяются внутренним давлением р внутр = 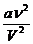 . В свою очередь, дополнительную внутреннюю энергию U' реального газа можно связать с работой сил внутреннего давления
. В свою очередь, дополнительную внутреннюю энергию U' реального газа можно связать с работой сил внутреннего давления
dU' = dA = р внутр dV = 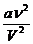 dV. (12)
dV. (12)
После интегрирования
U' = 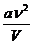 (13)
(13)
Для полной внутренней энергии ν молей реального газа, имеем
U = vCVT + U' = vCVT – 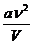 . (14)
. (14)
Из выражения(13) следует, что внутренняя энергия газа Ван-дер-Ваальса зависит не только от его температуры, как в случае с идеальным газом, но и от объема, занимаемого им. По этой причине при изотермическом процессе в газе Ван-дер-Ваальса изменяется его внутренняя энергия. При этом подведенная к газу теплота не равна совершенной им работе.
Эффект Джоуля – Томсона
В случае медленно протекающего адиабатического расширения реального газа при изменении давления от р 1 к р 2 происходит изменение температуры. Это явление получило название эффекта Джоуля – Томсона, а сам процесс – процессом Джоуля – Томсона. Эффект Джоуля – Томсонашироко используется, например, при сжижении газов.
На рисунке 4 изображена схема неравновесного расширения газа в адиабатических условиях: на рис. 4, а – начальное состояние системы, рис. 4, б – конечное. В середине цилиндра, помещенного в адиабатическую оболочку, находится перегородка С (узкая щель, пористое тело, дроссель и т. п.), препятствующая быстрому прохождению газа.
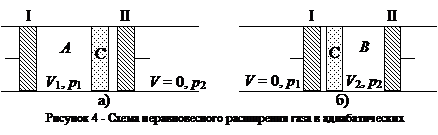 |
Из части А поршнем I через перегородку под давлением р 1, продается газ, в результате чего объем газа изменяется от V 1до нуля, При этом в части В перемещается поршень II и объем газа при постоянном давлении изменяется от нуля до V 2. Так как давления р 1и р 2постоянны в части А газ совершает работу р 1(0 – V 1) = -р 1 V 1, а в части В работу
р 2 (V 2– 0) = p 2 V 2.(15)
Будем считать, что внутренняя энергия системы изменяется на величину U 2– U 1.
Запишем для этого процесса первое начало термодинамики
Q = U 2 - U 1 + p 2 V 2 - р 1 V 1.(16)
Так как процесс адиабатический (Q = 0), то
U 1 + р 1 V 1 = U 2 + p 2 V 2. (17)
Отсюда следует, что в процессе Джоуля – Томсона энтальпиясистемы (U + рV) не изменяется: Н 1 = Н 2 = const.
Здесь Н 1и Н2 – энтальпии, соответствующие начальному и конечном стояниям системы.
Для идеального газа U = c VmТ и 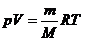 , отсюда энтальпияpaвна
, отсюда энтальпияpaвна
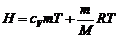 (18)
(18)
Таким образом, энтальпиядля постоянной массы газа зависит только от температуры.
Для определения изменения температуры одного моля газа преобразуем равенство (17), сделав некоторые упрощения. В левой части давление 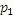 большое, поэтому газ здесь будем считать реальным, а в правой части давление
большое, поэтому газ здесь будем считать реальным, а в правой части давление 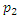 невелико и, следовательно, газ можно считать идеальным. Следовательно
невелико и, следовательно, газ можно считать идеальным. Следовательно
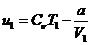 (19)
(19)
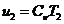 (20)
(20)
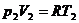 (21)
(21)
Из уравнения Ван-дер-Ваальса
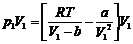 (22)
(22)
Подставим (19-22) в формулу (17)
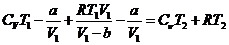 (23)
(23)
Третье слагаемое можно записать в виде
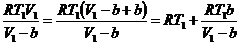 (24)
(24)
С учетом этого преобразования уравнение (23) примет вид
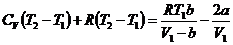 (25)
(25)
Отсюда получим формулу для изменения температуры газа при протекании через пористую перегородку
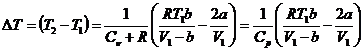 (26)
(26)
Как видно, знак DT определяется знаком выражения, стоящего в скобках.
Из формулы (26) видно, что для идеального газа (поправки а и b равны 0) DT =0 то есть температура идеального газа при таком расширении не меняется, т.е эффект Джоуля-Томсона отсутствует.
Температура реальных газов в таком процессе может как понижаться Δ T < 0 (положительный эффект Джоуля - Томсона), так и повышаться Δ T > 0 (отрицательный эффект Джоуля - Томсона).
С молекулярно-кинетической точки зрения знак эффекта Джоуля Томсона зависит от того, какая из постоянных Ван-дер-Ваальса (а или b),играет более существенную роль. Другими словами, какой фактор ”неидеальности” газа при данной температуре преобладает: силы притяжения или размер молекул.
Если можно пренебречь поправкой а (а=0), то DT >0, T2>T1, т.е при расширении газ нагревается. Это отрицательный эффект Джоуля -Томсона.
Если можно пренебречь поправкой b (b=0), то DT <0, T2<T1и газ охлаждается. Это положительный эффект Джоуля- Томсона.
Существует температура газа Тi, называемая температурой инверсии, при которой Δ T = 0. Газ, имеющий температуру выше температуры инверсии, нагревается, ниже – охлаждается.
Температура инверсии зависит от давления и свойств газа.
При одной и той же температуре некоторые газы могут нагреваться, а другие охлаждаться. Например, при комнатной температуре и невысоком давлении воздух в процессе Джоуля – Томсона охлаждается, тогда как для кого же эффекта водород следует охладить до 200 К, а гелий – до 40 К.
Для количественной оценки эффекта при малых перепадах температур Δ T и давлений Δ р вводится коэффициент Джоуля – Томсона
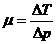 (27)
(27)
Применительно к газу, подчиняющемуся уравнению Ван-дер-Ваальса и при некоторых упрощающих предположениях этот коэффициент равен
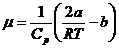 (28)
(28)
где а и b – постоянные Ван-дер-Ваальса, Ср – молярнаятеплоемкость при постоянном давлении, R – молярнаягазовая постоянная, Т – температура продавливаемого газа.
Перепад давлений всегда отрицателен (рисунок 4): Δρ < 0. Следовательно, при положительном эффекте Джоуля – Томсона ΔТ < 0, µ > 0, а при отрицательном эффекте ΔT > 0, µ < 0.
Температуре инверсии соответствует µ = 0, отсюда из (28) имеем
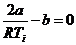 , или
, или 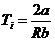 . (29)
. (29)
Из соотношения (29) видно, что чем большую роль играют силы притяжения между молекулами (больше а) и чем меньшую роль играет размер молекул (меньше b), тем выше температура инверсии.
Положительному эффекту Джоуля – Томсона соответствует условие 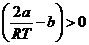 , которое реализуется, например, при b = 0.
, которое реализуется, например, при b = 0.
Это объясняется тем, что при расширении увеличивается потенциальная энергия сил притяжения и, соответственно, уменьшается кинетическая энергия молекул, т. е. температура.
Отрицательному эффекту Джоуля – Томсона соответствует условие 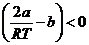 , которое реализуется, например, при а = 0.
, которое реализуется, например, при а = 0.
Физически это соответствует отсутствию межмолекулярных сил притяжения, а постоянная b,связанная с размером молекул, может ассоциироваться с межмолекулярными силами отталкивания, так как такие силы действуют при сближении молекул.
Таким образом, при расширении уменьшается потенциальная энергия сил отталкивания и, соответственно, увеличивается кинетическая энергия теплового движения молекул, т. е. температура.
Так как критическая температура для реальных газов также выражается через поправки а и b (формула 11), то можно получить соотношение между температурой инверсии и критической температурой
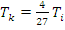 (30)
(30)
ЛАБОРАТОРНАЯ РАБОТА